二元函数求导公式_【高等数学】多元复合函数求导的基本方法

回顾：

一元复合函数

其求导有链式法则：

画出函数关系图：

，可见从

到

有一条路径，所以结果是 1 项的和，每一段路径（对应一个导数）乘起来。

这个规则推广到多元复合函数也是适用的。本篇就来讲一讲这个基本方法，掌握了它各种多元复合函数求导，包括各种隐函数求导，无论多复杂都手到擒来。

一. 基本步骤

非常简单：

（1）先理清函数关系，画出函数关系图；

（2）按照规则写出式子（有几条路径就是几部分的和，路径的每段对应的导数用乘法连起来）。

剩下的就只是计算，还要注意一元函数关系用直立的导，多元函数关系用偏导；还有通常的二元函数或多元函数（非隐函数，方程式才隐含隐函数），比如

, 其中的

是相互独立的，即

, 也即通常求偏导时，将其余变量当常数对待。

很多学生追求题海战术，往往忽略第一步，结果做了大量的题目，遇到难题还是不会。

二. 若干例子

下面通过几个例子来阐述。

例1

, 求

.

解：（1）分析函数关系，

是

的函数，

是

的函数

，据此画出函数关系图：

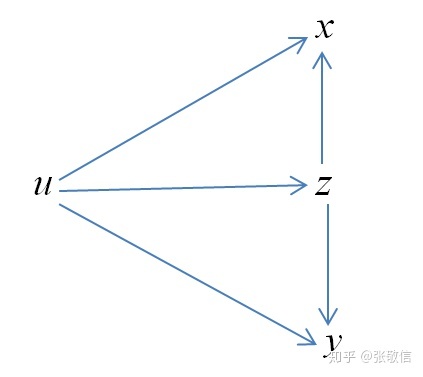
（2）按规则写出式子

到

有两条路径：

直接到

，

先到

再

到

（计算略)

注意：上式两个

的含义是不同的，左端的

是整个函数关系中的偏导关系，而右端的

只是这个分支路径的偏导关系，只考虑

对

的偏导，将

当常数对待。

说明：整个函数关系是指“复合之后

只是

的二元函数（不含中间变量）”，即

而将整个函数关系（含中间变量）表示成的上图，是对整个函数关系的一种分解，分解之后每部分关系都是相对独立的关系（不再混杂不清），即

故在按函数关系图写出式子时，不需要再考虑混杂关系，只需要按规则写即可。

例2 隐函数求导也一样，除了时刻注意到隐含的函数关系。比如，

,求

.

解：(1)

隐含了函数关系

. 【当然，根据问题需要，它也可以隐含函数关系：

】

先画出函数关系图（

是

的函数，

是

的函数）：

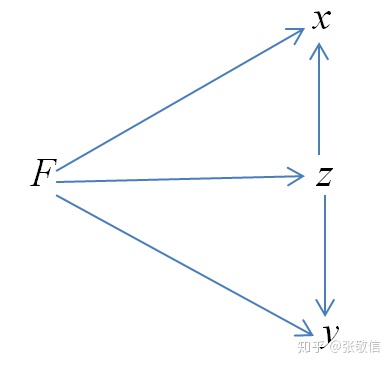
为了求

，两边同时对

求导，注意隐含的函数关系

.

按规则写出式子：

(2) 再求二阶偏导，按定义二阶偏导就是对一阶偏导结果，再求一次一阶偏导

，代入

画出函数关系图，注意

的地位与

是相同的，仍有相同的函数关系：

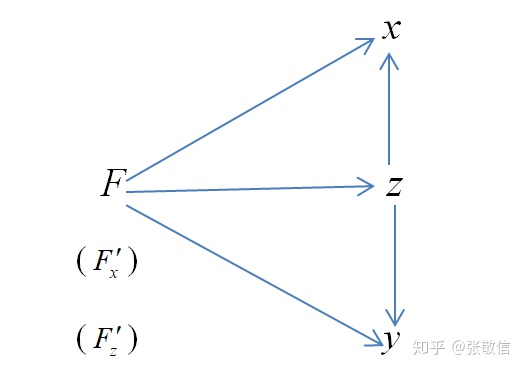
所以，上式先是商式求导，再注意到上图的函数关系，正常计算即可（略）。

例3 设

有二阶连续偏导，已知方程

, 求

.

解：（1）先理清函数关系

是方程式，所以这是个隐函数，其中有

，所以实际上是

, 它隐含的函数关系是

.

要求

， 那就是全微分公式，需要先求

又

中的两个位置变量带表达式，所以，先引入中间变量（复合函数）简化关系，令

, 则方程式变为

画函数关系图（别忘了隐函数关系）：

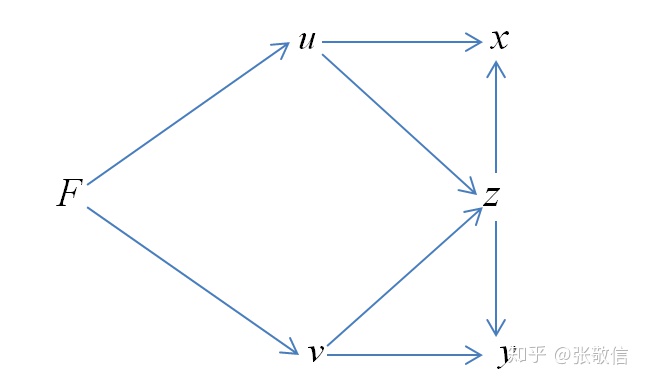
(2) 方程式两边

同时对

求导，按照上图和规则写式子：

到

共有 3 条路径：

到

到

,

到

到

到

,

到

到

到

. 故

是自己引入的中间变量，不是原题目里的，按照约定用位置下标来写，即计算上式得

可解出

同理，方程两边同时对

求导，可推得

(3) 于是，由全微分公式，可得

例4 方程组

分析：若从

解出

再代入

可得

, 该隐函数可隐含函数关系

; 同理，若先从第1个方程解出

再代入第2个方程，可确定隐函数函数关系

.

故该方程组隐含两个二元函数关系：

那么就可以求

.

画出函数关系图：

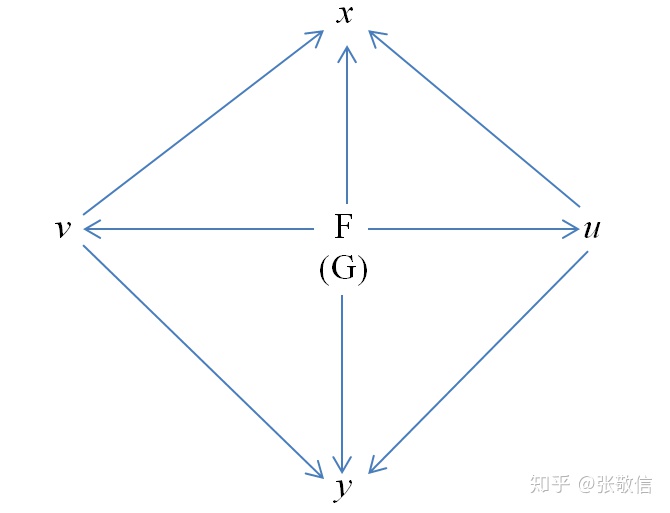
原方程组两边同时对

求导，根据上图和规则可得

即

解这个关于

的二元一次方程组，即可求得

.

同理，原方程组两边同时对

求导，解方程组可求得

.

总结：以上就是多元复合（隐）函数（无论有表达式还是无表达式）求导（包括求一阶、二阶导）的基本方法，通过一两道题掌握了这个基本方法，不用搞题海战术，这类题也都能轻松解决。

主要参考文献

高等数学，同济版。

————————————————————

原创作品，转载请注明。