t p
0 0
0.1 0.000153858117025703
0.2 0.00113635125058927
0.3 0.00354094536690505
0.4 0.00774995321171104
0.5 0.0139773127635119
0.6 0.0223045277665952
0.7 0.0327107264260888
0.8 0.045097671689982
0.9 0.0593104487096521
1 0.0751544603458374
1.1 0.0924092784480174
1.2 0.110839825729681
1.3 0.130205299190234
1.4 0.15026619013219
1.5 0.170789706946456
1.6 0.191553864152902
1.7 0.212350463947764
1.8 0.232987164068041
1.9 0.253288797556241
2 0.273098085483502
2.1 0.292275862412115
2.2 0.310700915949384
2.3 0.328269525810084
2.4 0.344894774052725
2.5 0.36050568631059
2.6 0.375046253659672
2.7 0.388474376039266
2.8 0.400760760679281
2.9 0.411887802626586
3 0.421848469056125
3.1 0.430645204473975
3.2 0.438288870057773
3.3 0.444797727137336
3.4 0.450196472109596
3.5 0.454515327832618
3.6 0.457789194688333
3.7 0.460056862986039
3.8 0.461360287149248
3.9 0.46174392114422
4 0.461254113832229
4.1 0.459938562326947
4.2 0.45784582098541
4.3 0.455024863331739
4.4 0.451524693986294
4.5 0.447394007531458
4.6 0.442680891173423
4.7 0.437432568044109
4.8 0.431695178017493
4.9 0.425513592980759
5 0.418931263594645
5.1 0.411990094692548
5.2 0.404730346598532
5.3 0.397190559785727
5.4 0.389407500444773
5.5 0.381416124683675
5.6 0.373249559233124
5.7 0.364939096682843
5.8 0.356514203423148
5.9 0.348002538610398
6.0 0.339429982614258
6.1 0.330820673538033
6.2 0.322197050530204
6.3 0.313579902725326
6.4 0.304988422765496
6.5 0.296440263959541
6.6 0.287951600235978
6.7 0.279537188137733
6.8 0.271210430191771
6.9 0.262983439065393
7.0 0.254867101993262
7.1 0.246871145025474
7.2 0.239004196707584
7.3 0.231273850858609
7.4 0.223686728163115
7.5 0.216248536338769
7.6 0.208964128681572
7.7 0.201837560827669
7.8 0.194872145603464
7.9 0.188070505865032
8.0 0.181434625253832
8.1 0.174965896818689
8.2 0.168665169474201
8.3 0.162532792283463
8.4 0.156568656568323
8.5 0.15077223586369
8.6 0.145142623743819
8.7 0.139678569558137
8.8 0.134378512122315
8.9 0.129240611417023
9.0 0.124262778352308
9.1 0.119442702659891
9.2 0.114777878979116
9.3 0.110265631204766
9.4 0.10590313516674
9.5 0.101687439712663
9.6 0.0976154862649487
9.7 0.093684126923875
9.8 0.0898901411876838
9.9 0.0862302513599292
10.0 0.0827011367130943
10.1 0.0792994464760622
10.2 0.0760218117113723
10.3 0.0728648561463187
10.4 0.0698252060199875
10.5 0.0668994990061887
10.6 0.0640843922700657
10.7 0.0613765697139019
10.8 0.0587727484653583
10.9 0.0562696846590641
11 0.0538641785601741
11.1 0.0515530790762085
11.2 0.0493332877012213
11.3 0.0472017619341055
11.4 0.0451555182106561
11.5 0.0431916343868713
11.6 0.0413072518088947
11.7 0.0394995770029831
11.8 0.0377658830169349
11.9 0.0361035104425343
12 0.034509868146757
12.1 0.0329824337377479
12.2 0.0315187537899174
12.3 0.0301164438509158
12.4 0.0287731882517283
12.5 0.02748673973969
12.6 0.026254918952848
12.7 0.0250756137527982
12.8 0.0239467784318853
12.9 0.0228664328094938
13 0.0218326612310501
13.1 0.0208436114823177
13.2 0.019897493630588
13.3 0.0189925788034449
13.4 0.0181271979149183
13.5 0.0172997403480255
13.6 0.0165086526019398
13.7 0.0157524369113125
13.8 0.0150296498446055
13.9 0.0143389008876741
14 0.0136788510182528
14.1 0.0130482112764632
14.2 0.0124457413359546
14.3 0.0118702480798271
14.4 0.0113205841850449
14.5 0.0107956467186572
14.6 0.0102943757487626
14.7 0.00981575297281662
14.8 0.00935880036556234
14.9 0.00892257884857201
15 0.00850618698312167
p1.jpg
(70.65 KB, 下载次数: 0)
2020-8-5 15:00 上传


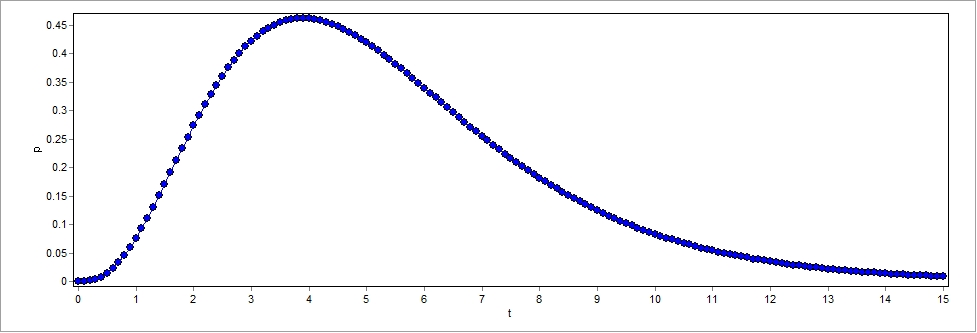




 这篇博客展示了如何在Matlab中计算一个上下限包含变量和参数的三重积分。通过逐步解析,展示了从设定积分范围到求解积分的过程,并给出了随着变量变化的积分结果,结果以表格形式呈现。
这篇博客展示了如何在Matlab中计算一个上下限包含变量和参数的三重积分。通过逐步解析,展示了从设定积分范围到求解积分的过程,并给出了随着变量变化的积分结果,结果以表格形式呈现。
















 4929
4929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








