含根式的定积分计算_考研数学：定积分计算体系要点详谈

最新推荐文章于 2021-02-05 08:17:30 发布

呀还差

最新推荐文章于 2021-02-05 08:17:30 发布

阅读量4k

点赞数

文章标签：含根式的定积分计算

本文链接：https://blog.csdn.net/weixin_34552961/article/details/112277963

版权

本文详细介绍了定积分计算体系，包括牛顿-莱布尼茨公式、换元法和分布积分法等基本方法，强调了定积分的性质和基本结论。文章还探讨了对称区间、周期函数、分部积分法的应用，并分类总结了常见题型，如基本型、对称区间类型、分段函数等，提供了识别特征和解题要点。最后，提醒考生要通过识别题型来确定解题策略，并进行大量练习以提高解题速度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

定积分计算体系详谈内容综述

基本方法
基本性质
基本结论与技巧
基本题型(每个类型的特征+解题要点)
如何用好题型问题简单谈谈。

本次文稿仅作为梳理问题，基于不定积分计算的前提下，希望能给人以帮助，在这一部分就统考的数学而言，个人建议可以借助题型分类，从而可以根据不同类型的题干本身的特征，快速定位题型，进而锁定方法方向，更有针对性解决问题。

要想定积分计算的快，准，易，除不定积分基础外，应当把该背的公式和方法梳理清楚。

定积分计算体系

基本方法

2.1 牛顿莱布尼茨公式

图片-02 牛顿莱布尼茨公式

前提条件请自己查。本来原函数存在，与定积分是否存在，但牛顿莱布尼茨公式建立起了两者的关系，给出了：用原函数求定积分的方法。 因此，不定积分计算必然是基础。

公式两步走：1.算原函数(不定积分)；2.代上下限
2.2 定积分的换元法(注意条件，涉及到个别题开根号之后取值正负)

图-03 摘选自《复习指南》

定积分换元法(3换步骤)：1.换元 x=g(t)；2.换微元：dx=dg(t)=g'(t)dt； 3.换上下限：x=a，则t=m;x=b,则t=n[一一对应]

相比不定积分换元法而言，定积分换元不需要回代，只用把对应的上下限值改掉即可。

图-04 摘选自《同济教材高数》

简化定积分换元手法：先凑微分，再平衡系数，将来换微元的时候就不用求导了。

图-05 简化定积分换元的一个手法

2.3 定积分的分布积分法

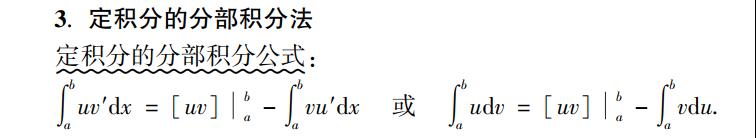
最低0.47元/天解锁文章