双曲线和直线联立公式_「代数思维系列」双曲线性质汇总

更正并致歉

首先：更正并致歉。在上一篇文章《椭圆性质汇总》中，有细心读者发现文中出现两处错误，现声明更正如下：

1，椭圆直径性质证明过程更正如下：

2，焦点三角形面积公式更正为：

本人再次对文章编辑过程中出现的错误致歉，希望大家持续关注并积极指正。

---

上一篇文章已对椭圆性质进行了汇总，本文对高考考点中涉及的双曲线的部分性质进行汇总。

注：以下仅讨论焦点在x轴上的双曲线性质。

双曲线定义

1.第一定义

平面内与两定点F1、F2的距离的差的绝对值为常数2a的动点P的轨迹叫做双曲线，其中2a

2.第二定义

平面内到定点F(±c，0)的距离和到定直线l：x=±a²/c的距离之比为常数e=c/a(e>1)的点的轨迹是双曲线。其中定点F(±c，0)为双曲线的左右焦点，定直线l：x=±a²/c为双曲线的左右准线。

对第二定义给出证明：

以右焦点和右准线为例：

上述定义即可作为判定定理也可作为性质定理。

双曲线方程

1.双曲线标准方程

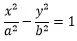
不再详述。

2.双曲线参数方程

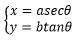
注：sec为正割函数，secθ=1/cosθ

其中θ为参数，θ的几何意义如下图：

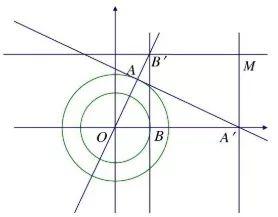
以双曲线实轴和虚轴为直径分别做圆C1(图中大圆)、C2(图中小圆)，对双曲线上任一点M，做x轴垂线，垂足为A'。过A'做圆C1切线，切点为A。过圆C2与x正半轴焦点B做圆C2的切线，与过M并平行于x轴的直线交于B'点。则O、A、B'三点共线，∠AOx即为参数θ。

切线

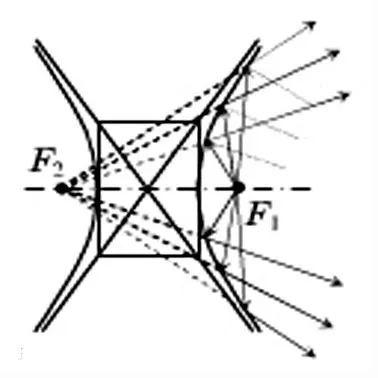
1.双曲线切线定理

双曲线的任意一条切线平分切点所在的焦点三角形顶角。

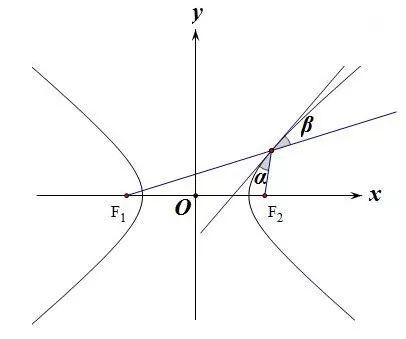
图中∠α=∠β，对顶角相等，切线是焦点三角形的一条角平分线。

证明从略。该性质在高考中应用较少，但其揭示了双曲线的一条光学性质，该性质在高中数学课本上也有提及，即从双曲线的一个焦点发出的光线，经双曲线反射后，其反向延长线在另一个焦点汇聚。

2.双曲线切线方程

过双曲线上一点P(x0，y0)的切线方程为：

以下用求导方法给出证明：

上述证明过程用到了隐函数求导，高中范围不涉及该知识点，有兴趣的同学可以尝试用二次函数判别式推导。

3.双曲线切点弦方程

过双曲线外一点，做双曲线上的两条切线(如果存在的话)，切点为A，B，则过A，B的切点弦方程为：

这里需要注意，过双曲线外(或上)一点做双曲线切线，最多只可能做两条切线。具体见下：

4.双曲线切线存在情况

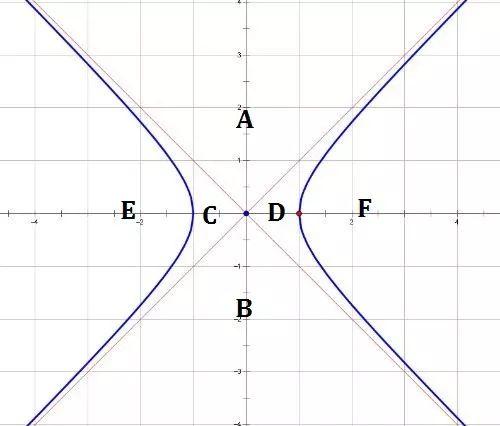
如图：双曲线及渐近线将平面分成ABCDEF六个区域：

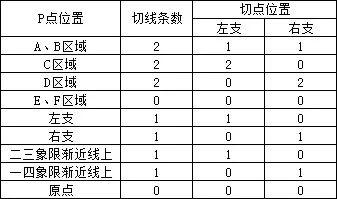
1.当P位于A、B区域时，过P可在双曲线两支各做一条切线；

2.当P位于C、D区域时，过P可在双曲线较近的一支做两条切线；

3.当P位于E、F区域时，过P不能做切线；

4.当P位于双曲线上时，过P只可在P点所在支做一条切线；

5.当P位于渐近线上(不含原点)时，过P只可在双曲线较近的一支做一条切线；

6.当P位于原点时，过P不能做切线；

具体列表如下：

直径

过双曲线中心的弦被称为双曲线的直径。实轴是双曲线最短的直径，双曲线直径可以无限长，故双曲线没有最长的直径。双曲线直径所在直线的斜率的绝对值必然小于渐近线斜率的绝对值。

1.双曲线直径性质

双曲线上的点与双曲线直径两端点连线的斜率(如果存在的话)之积是定值，定值为e²-1。

特别的：双曲线上任意点到实轴两端点连线斜率之积是定值e²-1。

2.双曲线直径长

双曲线直径长公式为：

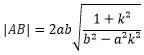
其中k为直径所在直线斜率。该公式请同学们自行推导。显然，直径存在的充要条件是|k|

特别的：当k=0时，上式结果为2a，即为实轴；当k趋于±b/a，即渐近线斜率时，上式结果趋于无穷大。

焦半径

1.焦半径长

焦半径长：|PF1|=|ex+a|，|PF2|=|ex-a|(F1，F2分别为左右焦点，P点在右支上时，等式右端绝对值内取正，P点在左支上时取负)。

通过准线定义证明，过程略。

2.焦半径性质

以短焦半径为直径的圆与以实轴为直径的圆外切，以长焦半径为直径的圆与以实轴为直径的圆内切。

以P点在右支上举例进行证明：

证：设以PF2为直径的圆的圆心为O2，则圆O2半径为r2=(ex-a)/2，

以长轴为直径的圆的圆心为坐标原点O，圆O半径为r=a，

两圆心距离|OO2|=(ex+a)/2=r+r2，

故以PF2为直径的圆与以长轴为直径的圆外切。

同理可证，以PF1为直径的圆与以长轴为直径的圆内切。

3.焦点弦

焦点弦长公式为：

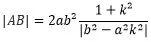
其中k为焦点弦所在直线斜率。该公式请同学们自行推导。

当|k|b/a时，焦点在焦点弦上，当|k|=b/a时，焦点弦不存在(或无限长)

特别的：当k=0时，上式结果为2a，即为实轴；当k趋于无穷大时，上式结果即为通径长：2b^2/a

4.焦点三角形

焦点三角形面积公式：

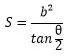
证明从略

双曲线与椭圆

双曲线两顶点A1，A2和与y轴平行的直线交双曲线的两动点P1,P2，直线A1P1与A2P2的交点轨迹为等轴椭圆。反之亦然。

其他

1.判别式

直线方程y=kx+m与双曲线方程联立后的，关于x的二次方程的判别式：

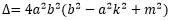
注：双曲线在联立方程时，首先要讨论b²-a²k²是否为0，如果为0，即直线斜率与渐近线斜率一致，则联立后关于x的方程为一次方程，不存在判别式问题。

2.一般弦长公式

双曲线一般弦长公式：

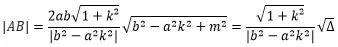
上述公式推导过程从略，显然，当m=0时，公式退化为直径公式；m=±kc，即直线过焦点时，公式退化为焦点弦公式；当|k|=b/a时，弦长不存在(或无限长)。

文|高见远，转载请注明出处。