x轴z轴代表的方向图片_方向导数与梯度

方向导数是对任意方向的导数，动态效果图：https://www.geogebra.org/m/MsqnxRqc，而偏导数是以x切面或y切面上的导数

假设z=f(x,y)为一曲面

为f定义内的一个点，如下图所示，设u为单位向量u=icosθ+jsinθ，并且平行于L

求u方向的方向导数斜率，可做一个通过P点平行于u方向的垂直平面，如下图所示，该垂直平面与曲面f(x,y)相交于曲线C,曲面在点

上沿着u方向移动到Q点(x,y,f(x,y))，连接点

与点Q(x,y)的直线方程用参数方程表示为：

( t为任意实数，Q(x,y)是直线L上任意一点)

备注：如下图所示，之所以用极坐标参数方程表示直线，是因为参数方程可以让直线在360度的任意方向上移动，而方向导数就是研究曲面在不同方向上的切线斜率

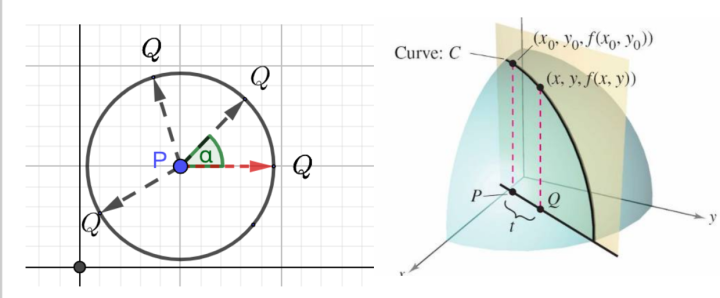
所以P与Q之间的距离为：

连接点

与

点的割线斜率可以写成

当

时，可以得到方向导数的定义

如果极限值存在，则沿着

方向的方向导数为该极值。

在求方向导数使用定义求解之外，还可以使用偏微分来简化计算

因为：

又因为函数z=f(x,y)可微，所以

由方向导数

公式可知是一个向量的形式表达，是在x轴方向上的变化分量与在y轴方向上的变化分量进行向量的相加，如下图所示

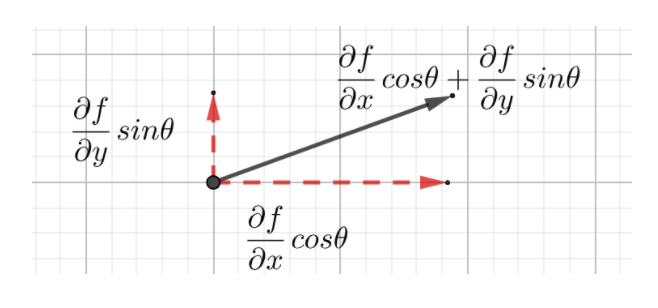
梯度概念理解：如下图所示，在p点放一个热源的等温线，则热源的辐射从里到外为10°、20°、30°、40°，若一个小蚂蚁在o点，要最快逃离热源，应该往oj方向逃离，若往om方向逃离则热源的变化率为0，即一直都是20°，也就是说蚂蚁一旦确定了某个逃离方向(0°,90°）方向角逃离，只要一直沿着该方向一直走，就是最快的热源降低的方向

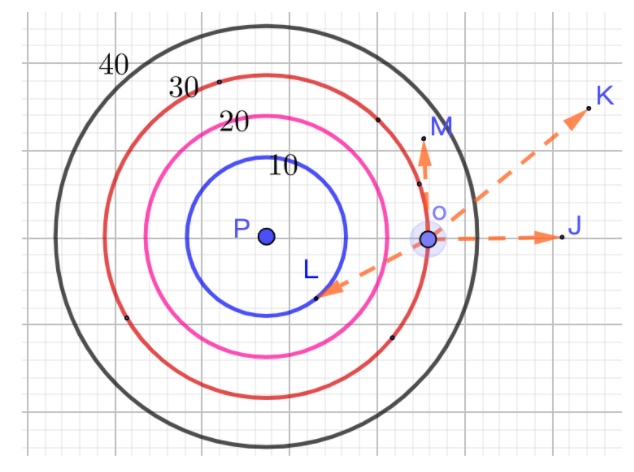
同理，一旦确定了方向导数的方向，沿着方向导数的方向就是梯度变化最快的方向，如下图所示，只要沿着PQ的方向角移动，则梯度下降得最快，就是最速降曲线

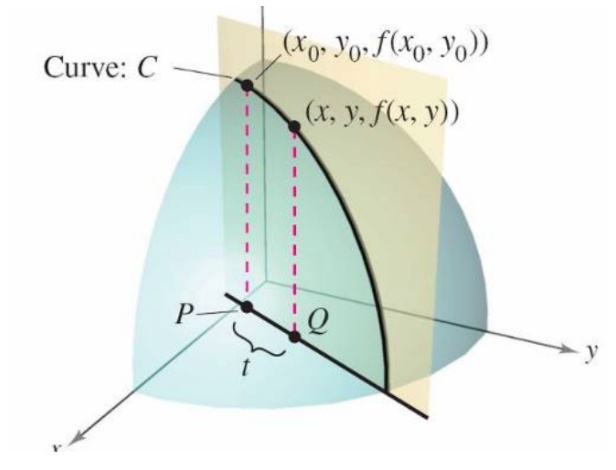
根据方向导数公式：

可以写成向量点乘的形式：

令：

因为

​

是单位向量

所以

当θ=0时， cosθ=1，所以

最大值的方向为

即沿着方向导数方向梯度变化最快

​