使用python构建向量空间_立体几何大题——向量法专题（空间直角坐标系构建）...

本期我们开始讲解立体几何大题中求解线线角、线面角和面面角的万能方法——向量法，该专题正男老师将分为三节进行精讲，分别是空间直角坐标系的构建、线线角和线面角的求解以及二面角的求解。在近六年的40份高考试题中，采用向量法对线线角、线面角和面面角的高考真题共出现38道，而采用向量法进行求解的基础是构建空间直角坐标系。因此，本期正男老师就构建空间直角坐标系的方法进行了梳理，2020年的高考题我们已经分析过了，所以本文中仅对2015-2019年的32道相关高考真题进行精讲，那我们就开始吧。

一、空间直角坐标系构建的方法分类

空间直角坐标系的构建的本质是首先在一个平面内寻找一对互相垂直的直线，再寻找垂直于该面的一条直线，最后通过平移的方法，寻找到三条直线的交点，如此以来就可以构建出一组两两垂直的空间直角坐标系。需要注意的是，在构建空间直角坐标系时，一定要遵循右手螺旋定则，否则会引起后面计算的错误，如图所示。

右手螺栓定则

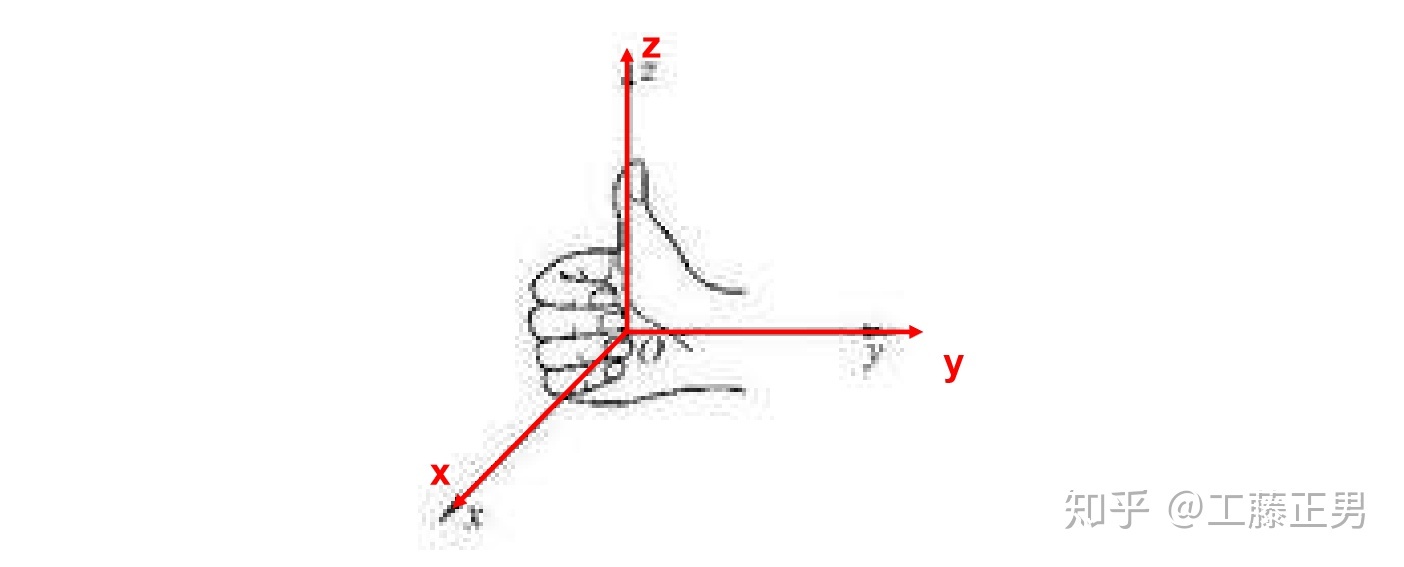
为方便后续讲解，按构建空间直角坐标系的难易程度，正男老师将2015-2019年内的31道高考真题分为了三类。第一类为低难度类，即题目中已经给出了空间线面垂直和底面线线垂直的关系；第二类为中难度类，即题目中仅给出了空间线面垂直和底面线线垂直中的任意一项的关系，未给出的一项，需要考生自行进行构造；第三类为高难度类，即题目中空间线面垂直和底面线线垂直均未给出，均需要考生自行进行构造。通常情况下第二类和第三类题目中均存在明显的面面垂直关系，有些是题目中已经给出，有些则需要考生自行进行证明。

此外，最难构建空间直角坐标系的题型是题目中给出的几何体不存在面面垂直关系，因此很难确定z轴的方向，该种设置会大大增加立体几何大题的整体难度。该类题型需要考生首先自行构建面面垂直后，随后在垂直于底面的平面中构建垂直于交线的直线，从而得到空间线面垂直关系，即可确定z轴方向。在2014-2020年的40份高考真题中仅出现过两次，分别为2017年浙江卷和2020年全国II卷。

二、低难度类

2015-2019年间有9道高考真题的空间直角坐标系构建难度较低，即已经给出了明确的空间线面垂直和底面线线垂直关系。该类型题目中的几何体通常为直棱锥和直棱柱（包括长方体），隐藏着线面垂直的关系；底面为直角三角形、矩形（包括正方形）、直角梯形和菱形（对角线互相垂直），隐藏着线线垂直的关系，下面逐题进行精讲。