二阶龙格库塔公式推导_[数学]龙格-库塔法

原理思想

要想求出非常近似的值，有种神器叫做泰勒公式 。泰勒给出了任意一个函数都可以用多项式逼近的方法求出函数值。这与常微分方程的数值方法的思想类似，就是已知初始值，借助导数这个工具，将其近似成求另一个点的坐标。龙格-库塔方法是用斜率的权重最后得到一个较好的斜率，然后求出函数值。

公式推导

以二阶推导为例

由泰勒公式：$$f(x)=\frac{f(x_0)}{0!}+\frac{f{'}(x_0)}{1!}(x-x_0)+\frac{f{''}(x_0)}{2!}(x-x_0)2+...+\frac{f{n}(x_0)}{n!}(x-x0)^n+R_n(x) \tag{1}$$

令\(x-x_0=h\),于是得\(x=h+x_0\),(1)式即可写成$$f(x_0+h)=\frac{f(x_0)}{0!}+hf{'}(x_0)+h2\frac{f{''}(x_0)}{2!}+...+hn\frac{f^{n}(x_0)}{n!}+R_n(h+x_0) \tag{2}$$

根据实际含义，已知初始点\((x_0,y_0)\),导函数\(y^{'}=f(x,y)\),则下个点\(y_{i+1}\)为多少？另h为步长，\(h=x_{i+1}-x_i\),所以(2)式,忽略到高阶项，可以写成$$y_{i+1}=y_i+hf(x_i,y_i)+\frac{h2}{2!}f{'}(x_i,y_i)+\mathcal{O}(h^3) \tag{}$$

因为y是x的函数，对x再求导，得到$$f^{'}(x_i,y_i)=\frac{\partial{f(x_i,y_i)}} {\partial{x}} + \frac{\partial{f(x_i,y_i)}} {\partial{y}}\frac{\mathrm{d}y}{\mathrm{d}x}$$

现在考虑二元的泰勒公式，有$$F(x+h,y+k)=F(x,y)+h\frac{\partial{F}}{\partial{x}}+k\frac{\partial{F}}{\partial{y}}+\mathcal{O}{(h2,k2)} \tag{3}$$

设\(k2=f(x_i+ph,y_i+qk_1h)\),则根据(3)式，得到$$k2=f(x_i+ph,y_i+qk_1h)=f(x_i,y_i)+ph\frac{\partial{f}}{\partial{x}}+qk_1h\frac{\partial{f}}{\partial{y}}+\mathcal{O}(h^2)$$

根据龙格-库塔的思想(斜率权重作为最终的斜率)，有\(y_{i+1}=y_i+h(ak_1+bk_2)\)，其中a，b是斜率的权重，带入\(k1=f(x_i,y_i)\)和k2,有$$y_{i+1}=y_i+haf(x_i,y_i)+hb\big[f(x_i,y_i)+ph\frac{\partial{f}}{\partial{x}}+qf(f_i,y_i)h\frac{\partial{f}}{\partial{y}}+\mathcal{O}(h^2) \big]$$

整理得:$$y_{i+1}=y_i+(a+b)hf(x_i,y_i)+h^2\big(bp\frac{\partial{f}}{\partial{x}}+bq\frac{\partial{f}}{\partial{y}}f(x_i,y_i)\big) + \mathcal{O}(h^3) \tag{}$$

比较这两个式子，()和(**),系数相等得到，$$a+b=1\bp=1/2\bq=1/2$$

这样四个未知数，三个方程，不难得到无穷多解，选择b=1/2,so a=1/2 p=q=1,于是$$y_{i+1}=y_i+h(\frac{1}{2}k_1+\frac{1}{2}k_2)$$

高阶的龙格库塔也是如此，先用泰勒公式求出三阶的或者四阶方程，然后求出每个斜率的表达式，最后比较系数得出方程组

常见的四阶龙格-库塔公式：$$k_1=f(x_i,y_i)\k_2=f(x_i+0.5h,y_i+0.5k_1 h)\k_3=f(x_i+0.5h,y_i+0.5k_2 h)\k_4=f(x_i+h,y_i+k_3 h)\y_{i+1}=y_i+h\big(\frac{1}{6}k_1+\frac{1}{3}k_2+\frac{1}{3}k_3+\frac{1}{6}k_4\big)$$

MATLAB 代码

fun = @(x,y) (x+y);

myans = rk_method(fun,0,2,1,0.25);

fprintf('result is %f\n',myans);

hold on;

% 准确值

xx = 0:0.25:1;

yy = 3*exp(xx)-xx-1;

plot(xx,yy,'r');

legend('近似值','point','准确值');

function re = rk_method(f,x0,y0,x,h)

n = round((x-x0)/h);

x = x0;

y = y0;

xx = [];

yy = [];

xx(1) = x;

yy(1) = y;

for i=1:n

k1 = f(x,y);

k2 = f(x+0.5*h,y+0.5*k1*h);

k3 = f(x+0.5*h,y+0.5*k2*h);

k4 = f(x+h,y+k3*h);

y = y+h*((1/6)*k1+(1/3)*k2+(1/3)*k3+(1/6)*k4);

x = x+h;

xx(i+1)=x;

yy(i+1)=y;

end

re = y;

plot(xx,yy,'b');

hold on;

scatter(xx,yy,'b*');

end

Result:

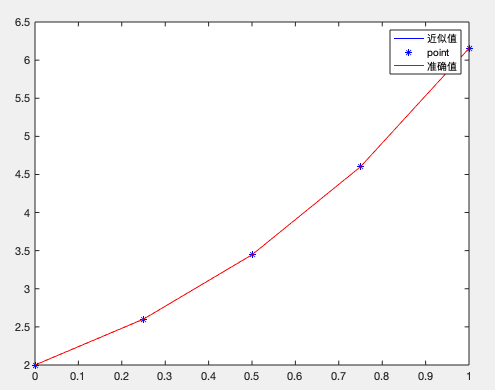
可以看出和matlab自带的函数图像已经重合了