圆锥曲线万能弦长公式_圆锥曲线11大常考题型&近5年真题汇总，想提分就赶紧收藏！...

或许，这就是数学的魅力吧，只需一二定理，三四公式，就可以命制出成百上千道不同的题目。

本文汇总了圆锥曲线11大常考题型，当然，最最重要的当属题型十一：存在性问题，一起来看~

圆锥曲线11大常考题型如下

题型一：数形结合确定直线和圆锥曲线的位置关系

题型二：弦的垂直平分线问题

题型三：动弦过定点的问题

题型四：过已知曲线上定点的弦的问题

题型五：共线向量问题

题型六：面积问题

题型七：弦或弦长为定值问题

题型八：角度问题

题型九：四点共线问题

题型十：范围问题(本质是函数问题)

题型十一：存在性问题(存在点、直线y=kx+b、实数、圆形、三角形、四边形等)

题型

题型一：数形结合确定直线和圆锥曲线的位置关系

题型二：弦的垂直平分线问题

题型三：动弦过定点的问题

题型四：过已知曲线上定点的弦的问题

题型五：共线向量问题

题型六：面积问题

题型七：弦或弦长为定值问题

题型八：角度问题

题型九：四点共线问题

题型十：范围问题(本质是函数问题)

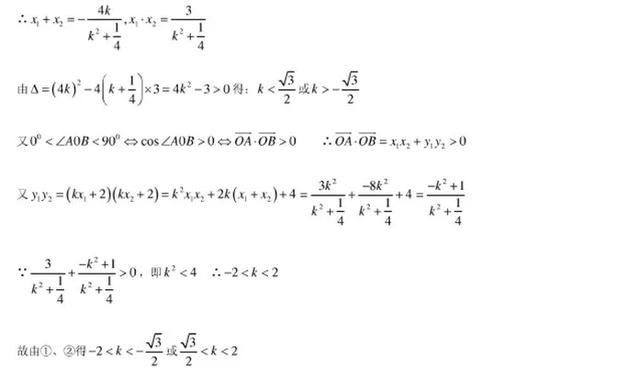
题型十一：存在性问题(存在点、直线y=kx+b、实数、圆形、三角形、四边形等)

举例

例1：

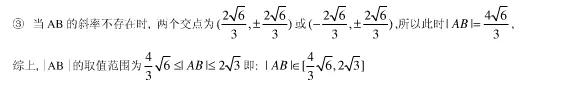
例2：

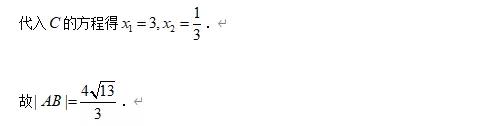
例3：

例4：

例5：

例6：

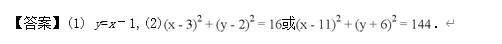
刷有所得：确定圆的方程方法

(1)直接法：根据圆的几何性质，直接求出圆心坐标和半径，进而写出方程。

(2)待定系数法

①若已知条件与圆心和半径有关，则设圆的标准方程依据已知条件列出关于的方程组，从而求出的值；

②若已知条件没有明确给出圆心或半径，则选择圆的一般方程，依据已知条件列出关于D、E、F的方程组，进而求出D、E、F的值。

例7：

答案：

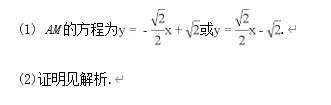
解析：

刷有所得：该题考查的是有关直线与椭圆的问题，涉及到的知识点有直线方程的两点式、直线与椭圆相交的综合问题、关于角的大小用斜率来衡量，在解题的过程中，第一问求直线方程的时候，需要注意方法比较简单，需要注意的就是应该是两个，关于第二问，在做题的时候需要先将特殊情况说明，一般情况下，涉及到直线与曲线相交都需要联立方程组，之后韦达定理写出两根和与两根积，借助于斜率的关系来得到角是相等的结论.

例8：

解析：

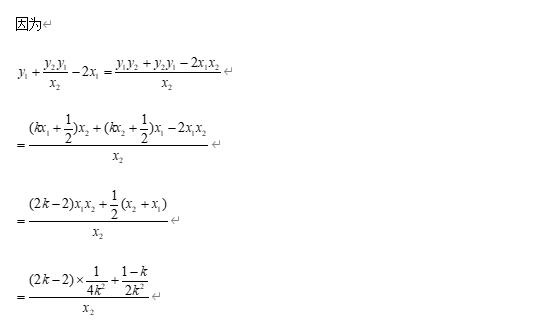
定点问题

例9：

解析：

例10：

例11：

解析：

例12：

例13：

答案：

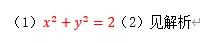
例14：

例15：

解析：

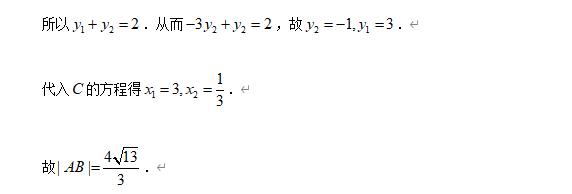
离心率问题

例16：

答案：D

解析：

刷有所得：椭圆定义的应用主要有两个方面：一是判断平面内动点与两定点的轨迹是否为椭圆，二是利用定义求焦点三角形的周长、面积、椭圆的弦长及最值和离心率问题等；“焦点三角形”是椭圆问题中的常考知识点，在解决这类问题时经常会用到正弦定理，余弦定理以及椭圆的定义.

例17：

答案：C

解析：

例18：

答案：C

解析：

刷有所得：求离心率的值或范围就是找的值或关系。由想到点M的轨迹为以原点为圆心，半径为的圆。再由点M在椭圆的内部，可得，因为 。所以由得，由关系求离心率的范围。

例19：

答案：A

解析：

刷有所得：本题主要考查椭圆的定义及离心率以及双曲线的定义及离心率，属于中档题. 离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出，从而求出;②构造的齐次式，求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解．

例20：

答案：D

解析：

例21：

答案：A

解析：

刷有所得：解决椭圆和双曲线的离心率的求值及取值范围问题，其关键就是确立一个关于的方程或不等式，再根据的关系消掉得到的关系式，而建立关于的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.

例22：

答案：A

解析：

刷有所得：

例23：

答案：A

解析：

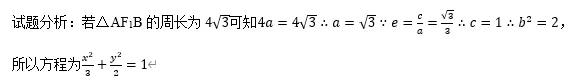
例24：

例25：

例26：

答案：C

解析：

例27：

例28：

答案：C

解析：

例29：

例30：

答案：D

解析：

例31：

例32：

例33：