怎么看函数帮助_中考压轴题专题｜含参二次函数范围问题怎么突破？看这一篇就够了...

在之前的文章中我们提到过，含参数的二次函数是中考压轴题的高频考点，往往是学生分数拉开差距的题型。

它不仅能考查学生对函数综合知识的掌握程度和灵活运用能力，而且还对分类讨论和数形结合两种数学思想方法有着较高的要求。

这类试题虽然知识和方法为学生所熟悉，似乎并不难解，但往往头绪纷繁，且计算量大，出错率较高。

一般来说，含参二次函数主要考查的是二次函数的图象和相关的性质，常考的题型有以下五种：

1判断含参二次函数的大致图象；

2求含参二次函数与x轴的交点问题；

3求含参二次函数的表达式；

4含参二次函数的对称性、顶点和最值问题；

5与含参二次函数相关的范围问题。

在之前的文章中，我们已经对第1-4类题型进行了方法的归纳与总结(参看往期文章《中考压轴题专题｜含参数的二次函数解题攻略》与《中考压轴题专题｜含参二次函数这样解，一点也不难！》)，今天我们将继续讲解第5类题型。

因全省统一中考的大趋势，笔者就以浙江杭州为例，分析了2016-2019年的杭州中考大数据，与含参二次函数相关的范围问题，即第5类题型考查的具体情况如下表：

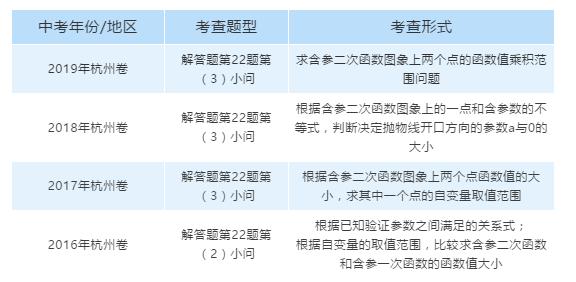
从表格中可以看到，杭州市近4年中考中，与含参二次函数相关的范围问题是每年的必考点，且始终位于解答题倒数第2题位置进行考查，其重要性不言而喻。

接下来我们就对第5类题型，也是在解答题压轴题中出现频率最高、难度也相对较高的题型，进行解题技巧的详细分析和方法的归纳。

一、真题分析

【例1】(2019·湖州)已知抛物线y=2x²－4x+c与x轴有两个不同的交点．

(2)若抛物线y=2x²－4x+c经过点A(2，m)和点B(3，n)，试比较m与n的大小，并说明理由．

解题思路

求出抛物线对称轴为直线x=1，根据点A(2，m)和点B(3，n)与对称轴的位置关系，再由函数的增减性即可求解．

解题步骤

解：∵x=－b/2a=－(－4)/2×2=1

∴抛物线y=2x²－4x+c的对称轴为直线x=1，

∴A(2，m)和点B(3，n)都在对称轴的右侧，

∵2>0，抛物线开口向上，

∴当x≥1时，y随x的增大而增大，

∴m

【例2】(2019·嘉兴舟山)小飞研究二次函数y=－(x－m)²－m+1(m为常数)性质时得到如下结论：

①这个函数图象的顶点始终在直线y=－x+1上；

②存在一个m的值，使得函数图象的顶点与x轴的两个交点构成等腰直角三角形；

③点A(x₁，y₁)与点B(x₂，y₂)在函数图象上，若x₁2m，则y₁

④当－1

其中错误结论的序号是( )

A．① B．②

C．③ D．④

解题思路

本题中考查与含参二次函数相关的范围问题的为结论③和④，故以下只分析这两个结论：

③把点A(x₁，y₁)与点B(x₂，y₂)代入已知的含参二次函数顶点式中，再计算y₁－y₂，然后进行因式分解，可以分离出和已知有关的x₁+x₂因式，再根据已知的范围，可以确定y₁－y₂与0的大小，进而比较出y₁和y₂的大小；

④根据已知的含参二次函数顶点式，可以确定该抛物线的开口方向和对称轴，然后按照要求，把符合要求的那一段图象做好标记，由这一段图象和对称轴的位置关系，列出不等式即可求出m的取值范围．

解题步骤

二次函数y=－(x－m)²－m+1(m为常数)

③由已知得y₁=－(x₁－m)²－m+1，y₂=－(x₂－m)²－m+1，

∴y₁－y₂=－(x₁－m)²－m+1－[－(x₂－m)²－m+1]

=(x₂－m)²－(x₁－m)²

=[(x₂－m)+(x₁－m)][(x₂－m)－(x₁－m)]

=(x₁+x₂－2m)(x₂－x₁)

又∵x₁2m

∴x₁+x₂－2m>0，x₂－x₁>0，

∴y₁－y₂>0，即y₁>y₂

故结论③错误；

④∵二次函数y=－(x－m)²－m+1(m为常数)的对称轴为直线x=m

且a=－1<0

∴抛物线开口向下，当x≤m时，y随x的增大而增大，

已知当－1

∴当－1

故m的取值范围为m≥2．

故结论④正确．

故选：C．

【例3】(2019·杭州)设二次函数y=(x－x₁)(x－x₂)(x₁，x₂是实数)．

(3)已知二次函数的图象经过(0，m)和(1，n)两点(m，n是实数)，当0

解题思路

将已知(0，m)和(1，n)两点代入函数y=(x－x₁)(x－x₂)求出m，n的值，再表示出mn，易得mn是关于x₁和x₂的代数式，再将此代数式中的两个变量x₁和x₂进行分离，变形，结合已知0

解题步骤

解：

二次函数的图象经过(0，m)和(1，n)两点，

∴m=x₁x₂，n=1－x₁－x₂+x₁x₂，

∴mn=x₁x₂(1－x₁)(1－x₂)

=(x₁－x₁²)(x₂－x₂²)

=[－(x₁－1/2)²+1/4][－(x₂－1/2)²+1/4]

∵0

∴0

∵m与n不能同时取到1/4，

∴0

【例4】(2018·杭州)设二次函数y=ax²+bx－(a+b)(a，b是常数，a≠0)．

(3)若a+b<0，点P(2，m)(m>0)在该二次函数图象上，求证：a>0．

解题思路

把x=2代入解析式，用ab表示m，由m的范围结合a+b>0可求a的取值范围．

解题步骤

解：当x=2时

m=4a+2b－(a+b)=3a+b>0①

∵a+b<0

∴－a－b>0②

①②相加得：

2a>0

∴a>0．

【例5】(2017·杭州)在平面直角坐标系中，设二次函数y₁=(x+a)(x－a－1)，其中a≠0．

(3)已知点P(x₀，m)和Q(1，n)在函数y₁的图象上，若m

解题思路

根据解析式，画出二次函数的大致图象，明确其增减性，根据图象可得答案．

解题步骤

解：y₁的对称轴为：直线x=(x₁+x₂)/2=(－a+a+1)/2=1/2，

当P在对称轴的左侧(含顶点)时，y随x的增大而减小，

∵(1，n)与(0，n)关于对称轴对称，

由m

当P在对称轴的右侧时，y随x的增大而增大，

由m

综上所述：m

【例6】(2016·杭州)已知函数y₁=ax²+bx，y₂=ax+b(ab≠0)．在同一平面直角坐标系中．

(2)若函数y₂的图象经过y₁的顶点．

①求证：2a+b=0；

②当1

解题思路

①将函数y₁的解析式配方，即可找出其顶点坐标，将顶点坐标代入函数y₂的解析式中，即可得出a、b的关系，再根据ab≠0，整理变形后即可得出结论；

②由①中的结论，用a表示出b，再将两个含参函数的解析式作差，即可得出y₁－y₂=a(x－2)(x－1)，根据x的取值范围可得出(x－2)(x－1)<0，分a>0或a<0两种情况考虑，即可得出结论．

解题步骤

①证明：∵y₁=ax²+bx=a(x+b/2a)²－b²/4a，

∴函数y₁的顶点为(－b/2a，－b²/4a)，

∵函数y₂的图象经过y₁的顶点，

∴－b²/4a=a(－b/2a)+b，即b=－b²/2a，

∵ab≠0，

∴－b=2a，

∴2a+b=0．

②解：∵b=－2a，

∴y₁=ax²－2ax=ax(x－2)，y₂=ax－2a= a(x－2)，

∴y₁－y₂=a(x－2)(x－1)．

∵1

∴x－2<0，x－1>0，(x－2)(x－1)<0．

当a>0时，a(x－2)(x－1)<0，y₁

当a<0时，a(x－2)(x－1)>0，y₁>y₂．

二、方法归纳

根据以上6个考查与含参二次函数相关的范围问题的中考真题，我们可以将此类问题分为三大类：01求参数的范围或自变量的范围

通常情况下，此类问题中的抛物线开口方向确定，对称轴直线方程中含1个参数或最后可以化为1个参数。

此时只需画出抛物线的大致图象，标出和参数有关的对称轴，再根据题意把符合条件的图象做好标记，很容易根据符合题意的图象列出与之有关的不等式，最后求出参数的范围或直接写出自变量的范围。

02求函数值的乘积范围

对于此类问题，首先将所求函数值的乘积表示成和参数有关的代数式(即把点的坐标代入对应的函数解析式)；

如果乘积中只含有1个参数，结合已知条件或已经求出的参数范围，求出该代数式的范围即可；

如果乘积中含有2个变量，则需分离变量，把代数式化成两个变量分开的式子，分别求出对应的范围， 即可求出整个代数式的范围。

03比较函数值的大小

此类问题不管是同一个函数图象上的不同点比较函数值大小，还是不同函数图象上已知自变量范围比较函数值大小，如果根据题意可以确定符合题目要求的图象，则可直接画图象确定函数值的大小；如果不能确定图象，则可采取函数值作差比较法。

使用图象法确定函数值大小相对较简单，此处不作详细介绍。下面对作差比较法的详细步骤进行说明：

a把需要比较函数值大小的点的坐标代入对应的函数解析式，可以将函数值表示成与参数有关的代数式；

b将这两个表示成参数的函数值作差，得到一个和参数有关的多项式，然后进行因式分解；

c因式分解后一般都会出现和已知有关的因式，根据已知的关系式判断出该结果和0的大小 (大多数情况抛物线的开口方向需要分a>0或a<0两种情况讨论)，最后得出函数值的大小关系。

从以上方法归纳中，我们不难发现：对于与含参二次函数相关的范围问题，不管是哪类问题，都需要熟练掌握参数与二次函数的对称性和增减性之间的关系，会进行和参数有关的字母运算，尤其作差之后如何进行因式分解，进而产生和已知有关的因式。

最后附上二次函数对称性和增减性之间关系的表格，供大家复习与参考。(注：当a<0时，对称轴不变，增减性与a>0时相反。)

来源：创课教研院

文稿/黄小英

编辑/任雨晨