单摆运动属于什么现象_Processing作品：拉面与单摆波

啥是单摆波

简单地说，就是很多个摆长依次递减的波，在做自然摆动的时候，整体从侧面看所看到的各个摆运动组合刀一起所形成的形态。中学的时候学过单摆的运动周期就可以用来解释单摆波这种现象：

单摆运动的近似周期公式为： T=2π√( L/ g)，其中L是摆长。

从这个公式中，可以看出摆动周期T是摆长的函数，正比于√L 。那么不同摆长的摆的摆动周期就会不同。

具体视频效果也可以参考下面这两个链接：

物理之美——单摆波_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili

狐极客：【物理学】单摆波（Pendulum Waves）

单摆的运动分析

摆的受力分析

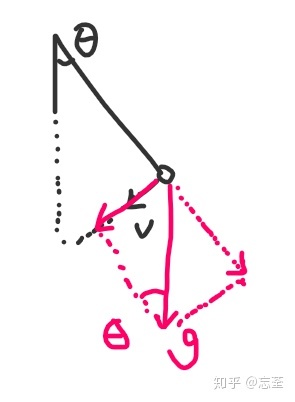
• 首先，对重力在圆周运行的切向进行分力 -g * sin(self.theta)。
• 然后把线加速度处以摆长算出角加速度 Atheta = -g * sin(self.theta)/ self.leng。
• 最后使用实时的角加速度用来更新角速度，再更新角度，就得到了最后的效果。
• 程序中没有用到摆长公式，因为摆长公式是对实时的角速度进行“积分”的某种结果，而我们的程序是实时演算的。

我的单摆波

知乎视频​www.zhihu.com

（简单地解释一下，为什么时间过去越久，和实际情况就差别越大：因为浮点数的计算误差随着时间在不断累积。一般单摆波再从有序到混乱之后还能恢复到有序状态，但是这里收到了计算误差的影响，所以就基本回不到有序的状态了）

完整代码

鼠标点击可以显示或者隐藏摆上的线。

g = 1e-1
strokeColor = False

class Bai():
    def __init__(self, leng, theta=30):
        self.theta = theta
        self.Vtheta = 0
        self.leng = leng
        
    def update(self):
        Atheta = -g * sin(self.theta) / self.leng
        self.Vtheta += Atheta 
        self.theta += self.Vtheta
        y, x = self.leng*cos(self.theta), -self.leng*sin(self.theta)
        line(0, 0, x, y)
        circle(x, y, 2)
        

bais = [Bai(i*0.3) for i in range(50, 900)]

def setup():
    size(600, 600)
    colorMode(HSB)
    
def draw():
    background(0)
    translate(width/2, height/2)
    for ind, b in enumerate(bais):
        if strokeColor:
            stroke(200, 30)
        else:
            noStroke()
        fill((ind/2)%255, 250, 250)
        b.update()
        
def mousePressed():
    global strokeColor
    strokeColor = not strokeColor