如何判断多项式有没有重根_如何判断在一点有没有导数？

导数是高等数学中的重要概念，什么是导数？

导数是变化率，如何表示？

设有函数y=f(x)，在x0点，自变量增量是△x,对应y的增量为△y,

则比率△y/△x 是y在△x上对x的变化率，而y在x0点的导数是

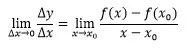
注意△y/△x是平均变化率，而f(x)在x0点的导数是在x0点的变化率,得用极限表示。

下面是判断在一点是否可导的方法：

一、在一点可导首先要连续

所谓连续就是变化不间断，不能有间断点。

二、初等函数在连续点一般是可导的

只要不是分段的函数，并且不是间断点，一般可导。

比如下面的求导公式：

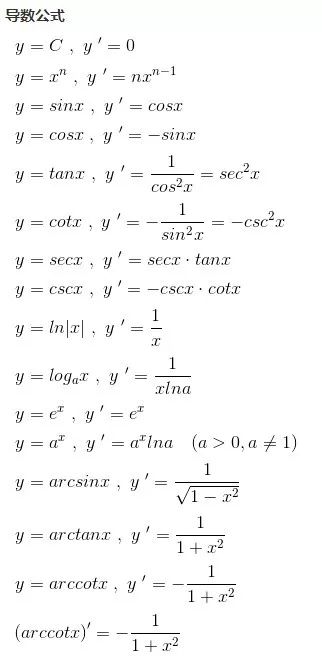
但在个别点的导数为无穷大，也可以说导数不存在，比如：

y=x^(1/3) 在x=0点就无导数,或者说导数无穷大，而y=x^3在0点导数为0

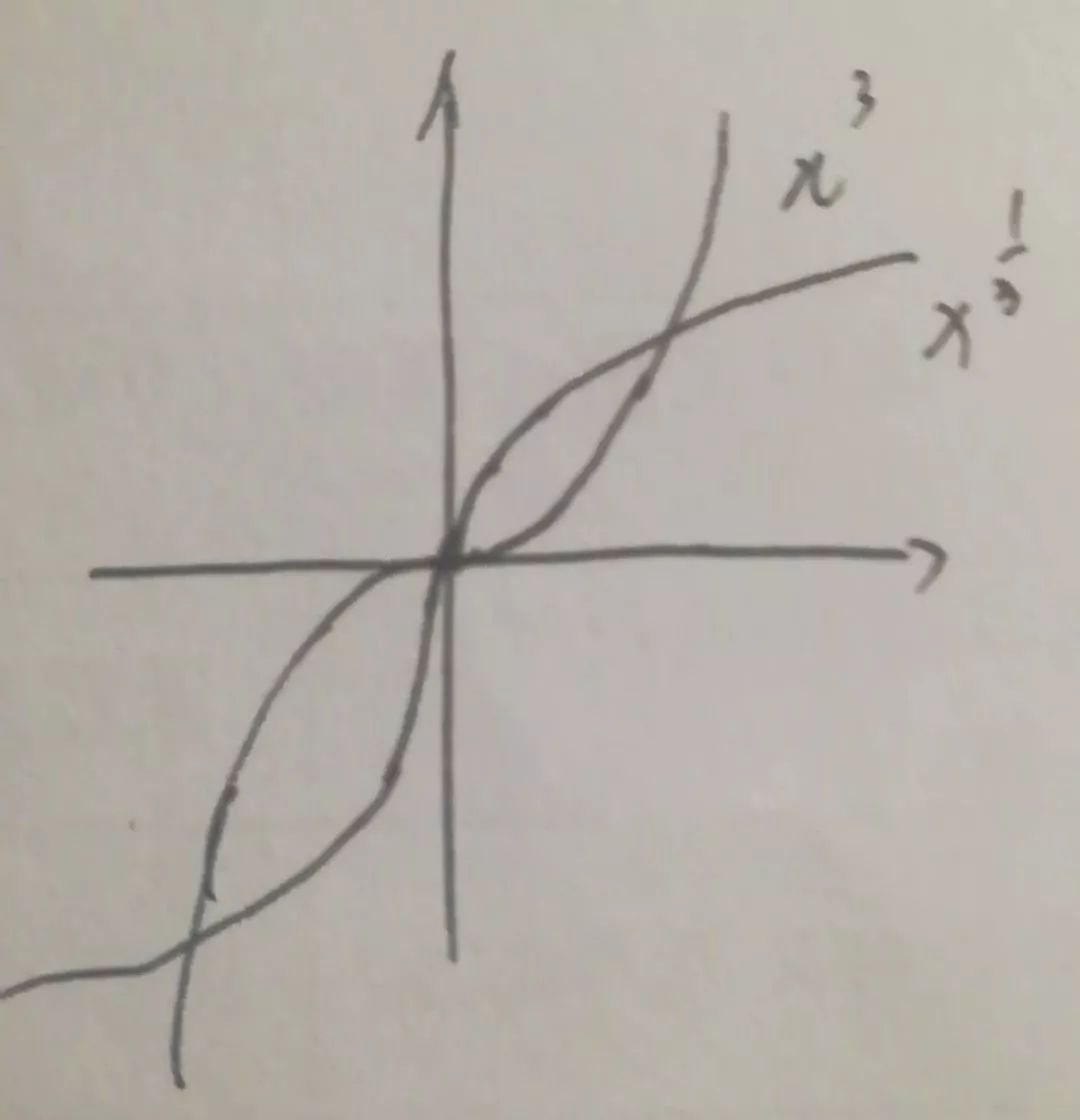
三、在图像上看有无切线来判断(分段函数连结点)

还有一个非常直观的方法就是看函数图像，如果在一点能画出切线则可导，如果切线是垂直x轴则认为不存在。

这对于判断分断函数非常好用，比如在尖点处不可导。

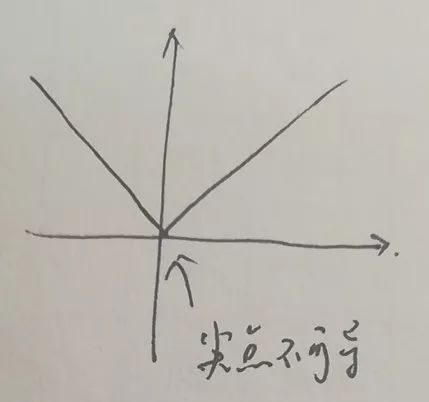
y=|x| 存在尖点

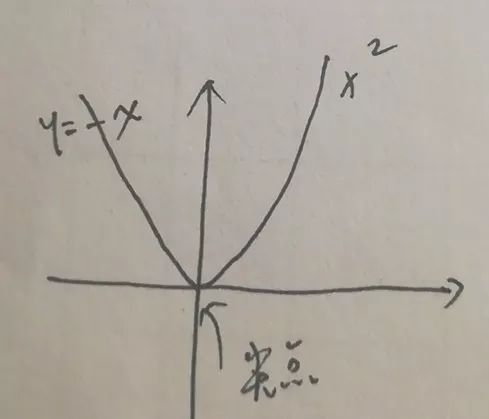
这个分段函数由y=-x与y=x^2组成，在连结点不存在切线。

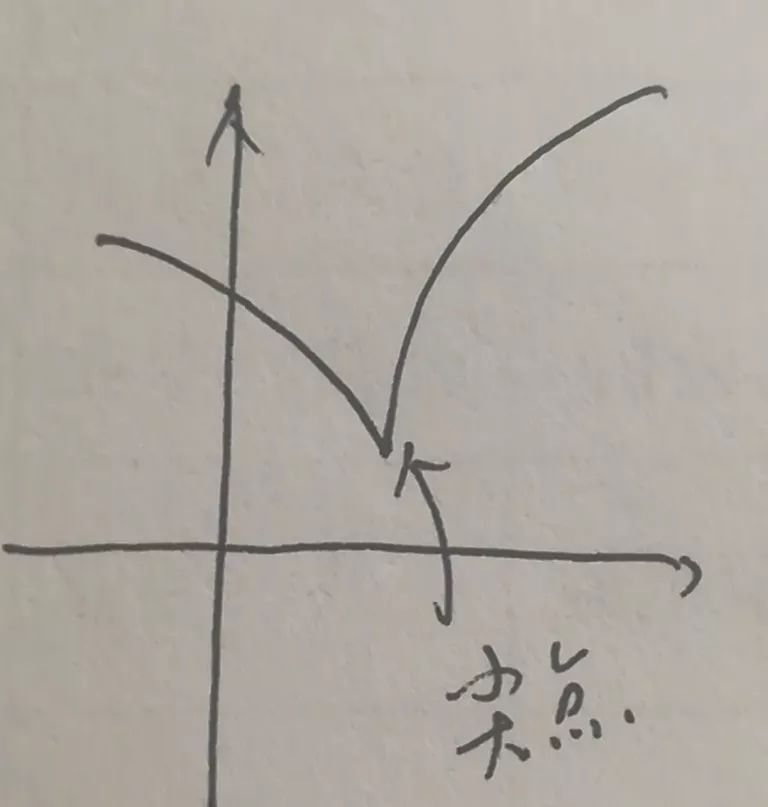
这个也是尖点，不存在切线。

四、分段函数连结点可导的判断依据

有时候只靠看还不行，眼见不一定真！

比如　y=x与y=x^2的组合

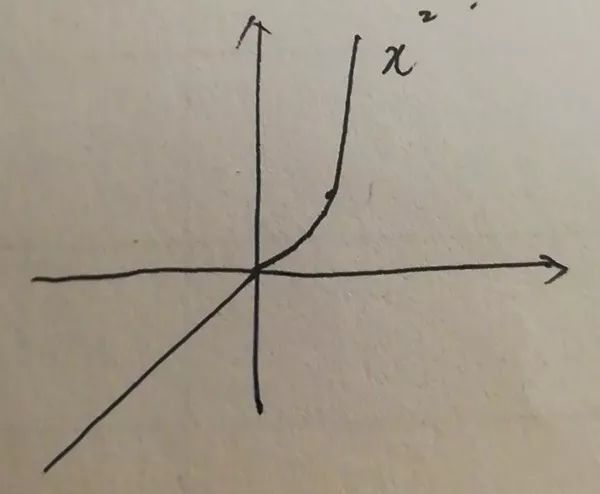
在x=0处导数不存在，这个点是尖点，但下图却不同

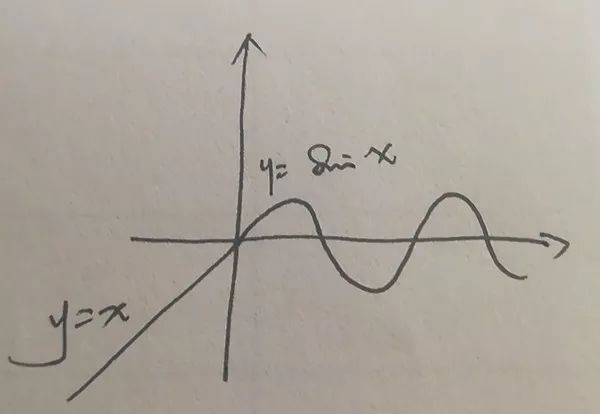
由y=x与y=sinx组合而成的这个函数在０点却是可导的，不是尖点，也就是说直线与曲线相连的点不一点都是尖点，没有切线，那么判断依据是什么呢？

判断这点的左右层数是否存在且相等，也就是说判断这点两边的函数在这点的变化率是不是相等。

y=x与y=x^2在０点的变化率不同，一个为1,一个为0,所以在0点不可导，而y=x与y=sinx在0处的变化率则是相同的，从图中也大致可以看出。

怎么样？在一点是否可导会不会判断了呢！