凸包学习笔记

于 2025-07-21 11:35:42 发布
阅读量25 收藏
点赞数
文章标签： 学习 笔记
合集 - 算法总结(24)
1. C D Q CDQ CDQ 分治总结 2.基环树算法总结 3.(抄自己luogu上的博客)莫队总结 4.珂朵莉树总结 5.虚树总结 6.从龟速乘到 M i l l e r − R a b i n Miller-Rabin Miller−Rabin 算法（数论算法总结） 7.浅谈李超线段树 8.浅谈长链剖分 9.浅谈平衡树 10.可持久化数据结构算法总结 11.线段树运用进阶 12.群论学习笔记 13.线性基学习笔记 14.LCT 学习笔记 15.原根学习笔记+BSGS复习笔记 16.多项式算法初探：从 FFT 到 NTT 17.下降幂、斯特林数学习笔记 18.多项式算法再探：FMT 和 FWT 19.min-max 容斥（最值反演）学习笔记 20.自适应 Simpson 积分法学习笔记 21.SAM 学习笔记 22.min_25 筛 学习笔记
23. 凸包学习笔记
24.2-SAT 学习笔记
收起

凸包，是指能包含点集中所有点的最小凸多边形（三维就是凸多面体）。显然，凸包的所有顶点都是点集中的点。凸包通常有两种出题套路，分别是计算几何（直接求有关凸包的信息）和决策单调性（类似于斜率优化 dp）。由于凸包本身并不好维护且不一定全都用得上，在信息学竞赛中，通常维护上凸壳或下凸壳。凸包可以有这两个凸壳拼接而得。下图是一只可爱的凸包：

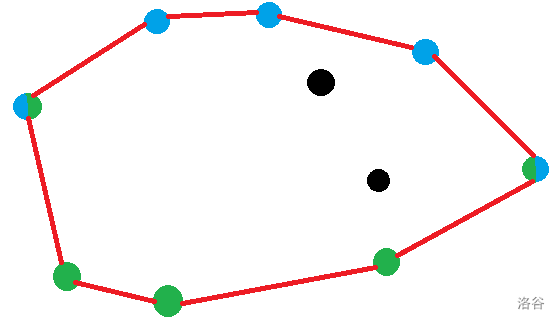
该图中，红线围起的多边形为凸包，蓝色点与其连线为上凸壳，绿色点与其连线为下凸壳。

一、凸包构建方法

注：该版块内容仅讨论上凸壳。

1.静态构建

首先，我们按照 \(x\) 轴坐标进行排序，然后按顺序一个一个插入点。

我们假设一条线段也是凸壳，那么我们先将前两个点加入上凸壳，然后考虑拓展这个上凸壳：

  1. 斜率减小
    下图就是一个斜率减小的例子：

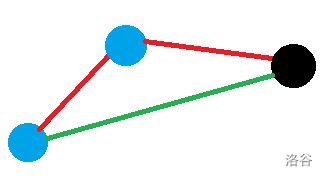
    此时，若采用绿色线段的模式，将第二个蓝色点扔出上凸壳，显然不符合凸包包含所有点的要求，所以直接加入黑点即可。同时，根据这一事实，我们也可以推断出：上凸壳每条边斜率递减。相对应的，下凸壳每条边斜率递增。
  2. 斜率增大
    下图就是一个斜率增大的例子：

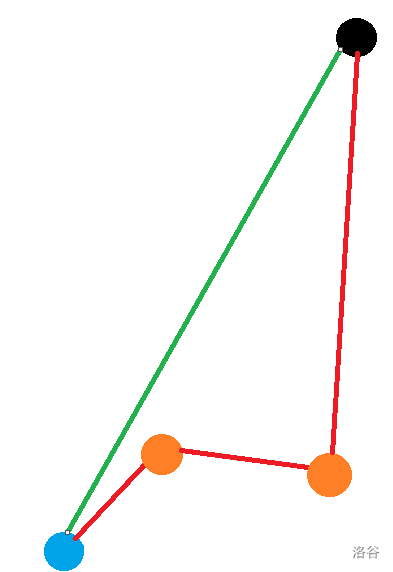
    我们发现，假如我们采取红色折线的模式，那么这个凸包就不是一个凸多边形了，所以要将第二个橘色点扔出上凸壳。同时要注意的是，假如仍然保留第一个橘色点，这个凸包也不是一个多边形，所以第一个橘色点也要舍去。说明在舍去一个点后，对于此时凸包最右侧的点是否保留，需要继续递归处理，直至上凸壳只剩两个点。

根据上述讨论，我们总结出了上凸壳的构建方式：

  1. 对所有点根据 \(x\) 坐标值进行升序排序。
  2. 直接加入前两个点。
  3. 将当前第二靠右的点 \(a\)，第一靠右的点 \(b\) 和当前枚举点 \(c\) 进行比较：
    1. 若当前上凸壳中点数为 \(1\)，跳出循环；
    2. 当线段 \((a,b)\) 的斜率大于线段 \((b,c)\) 的斜率时，直接加入点 \(c\)，跳出循环；
    3. 否则弹出 \(b\)，继续循环。

这和单调栈如出一辙。时间复杂度瓶颈为排序，因此时间复杂度为 \(O(n\log n)\)，单调栈部分则为 \(O(n)\)。假如要求时间复杂度非均摊，我们可以用二分找出进行完 \(3\) 操作后的栈顶，单次时间复杂度为 \(O(\log n)\)（这类题有 [NOI2014] 购票）。

cpp 

   //单调栈法

   #define dx(x,y) (xc[x]-xc[y])

   #define dy(x,y) (yc[x]-yc[y])

   int n,xc[N],yc[N],id[N],st[N],tp;

   int check(int x,int y,int z){

   	return dx(z,y)*dy(y,x)<=dy(z,y)*dx(y,x)

   }int cmp(int x,int y){

   	return xc[x]<xc[y];

   }int main(){

   	……………………………………

   	for(int i=1;i<=n;i++) id[i]=i;

   	sort(id+1,id+n+1,cmp);

   	for(int i=1;i<=n;st[++tp]=id[i++])

   		while(tp>1&&check(st[tp-1],st[tp],id[i])) tp--;

   }
cpp 

   //二分法（摘自本人 [NOI2014] 购票 代码）

   //实际上，不能均摊的情况基本上只有要求可撤销的时候。

   struct mstack{

   	int tp=-1;vector<int>st;

   	db sp(int x,int y){

   		return 1.0*(f[x]-f[y])/(d[x]-d[y]);

   	}int cmp(int x,int y,int z){

   		return sp(x,y)>=sp(y,z);

   	}void add(int x,int id){

   		int l=1,r=tp,ans=tp+1;

   		while(l<=r){

   			int mid=(l+r)/2;

   			if(cmp(st[mid-1],st[mid],x))

   				ans=mid,r=mid-1;

   			else l=mid+1;

   		}if(ans>tp) st.push_back(0);

   		sk[++ft]={id,tp,st[ans]},st[tp=ans]=x; 

   	}//插入

   	int ans(int x){

   		if(tp<0) return (int)9e18;

   		int l=0,r=tp-1,ans=st[tp];

   		while(l<=r){

   			int mid=(l+r)/2;

   			if(sp(st[mid],st[mid+1])>x)

   				ans=st[mid],r=mid-1;

   			else l=mid+1;

   		}return f[ans]-d[ans]*x;

   	}//查询

   };

2.动态加点

这个时候我们就不能按照刚才的方式事先排序了。因此我们需要一个能快速找到前驱后继，支持加点和删除的数据结构。视题目而言，可以采用 \(set\)（如 [HAOI2011] 防线修建）或各种平衡树进行维护（如 [NOI2007] 货币兑换）。

cpp 

   //set 版本（摘自本人 [HAOI2011] 防线修建 代码）

   //写 set 就要注意一些边界条件，以防 RE

   struct idx{int x;};

   int n,q,xc[N],yc[N];

   bool operator<(idx x,idx y){

   	return xc[x.x]==xc[y.x]?yc[x.x]<yc[y.x]:xc[x.x]<xc[y.x];

   }set<idx>s;

   int cmp(int x,int y){

   	return xc[x]==xc[y]?yc[x]<yc[y]:xc[x]<xc[y];

   }int check(int x,int y,int z){

   	return dy(y,x)*dx(z,y)<=dy(z,y)*dx(y,x);

   }void add(int x){

   	auto itl=s.lower_bound({x}),itr=itl;itl--;

   	if(check(itl->x,x,itr->x)) return;

   	while(1){

   		itl=s.lower_bound({x}),itr=--itl;

   		if(itr==s.begin()) break;itl--;

   		if(!check(itl->x,itr->x,x)) break;

   		s.erase(itr);

   	}while(1){

   		itr=s.upper_bound({x}),itl=itr++;

   		if(itr==s.end()) break;

   		if(!check(x,itl->x,itr->x)) break;

   		s.erase(itl);

   	}s.insert({x});

   }
cpp 

   //平衡树（此为 fhq-treap）版本

   //这个代码量就会很大，但更灵活，边角条件也没那么复杂

   const db eps=1e-6;

   int n;db mx;

   struct dot{db x,y;}fs,ed;

   namespace FHQ{

   	#define ls(x) pl[x].ls

   	#define rs(x) pl[x].rs

   	#define sz(x) pl[x].sz

   	#define rk(x) pl[x].rk

   	#define xc(x) pl[x].xc

   	#define yc(x) pl[x].yc

   	struct fhq{

   		int ls,rs,sz,rk;

   		db xc,yc;

   	}pl[N];int rt,tl;

   	int mk(db a,db b){

   		return pl[++tl]={0,0,1,rand(),a,b},tl;

   	}void push_up(int x){

   		sz(x)=sz(ls(x))+sz(rs(x))+1; 

   	}void spilt(int x,db sp,int &a,int &b){

   		if(!x) return a=b=0,void();

   		if(xc(x)<=sp) a=x,spilt(rs(x),sp,rs(x),b);

   		else b=x,spilt(ls(x),sp,a,ls(x));push_up(x);

   	}int merge(int x,int y){

   		if(!x||!y) return x|y;

   		if(rk(x)<rk(y)) return rs(x)=merge(rs(x),y),push_up(x),x;

   		return ls(y)=merge(x,ls(y)),push_up(y),y;

   	}void insert(db x,db y){

   		int a,b;spilt(rt,x,a,b);

   		rt=merge(merge(a,mk(x,y)),b);

   	}void erase(db x,db y){

   		int a,b,c;spilt(rt,x-eps,a,b);

   		spilt(b,x,b,c),rt=merge(a,c);

   	}int kth(int x,int k){

   		if(k<=sz(ls(x))) return kth(ls(x),k);

   		if(k==sz(ls(x))+1) return x;

   		return kth(rs(x),k-sz(ls(x))-1);

   	}int hv(dot x){

   		int a,b,c;spilt(rt,x.x,a,c);

   		spilt(a,x.x-eps,a,b);int re=sz(b);

   		return rt=merge(merge(a,b),c),re;

   	}

   }dot pre(dot x,db dl=0){

   	int a,b;FHQ::spilt(FHQ::rt,x.x-dl,a,b);

   	int kt=FHQ::kth(a,FHQ::sz(a));dot re={FHQ::xc(kt),FHQ::yc(kt)};

   	return FHQ::rt=FHQ::merge(a,b),re;

   }dot nxt(dot x,db ad=0){

   	int a,b;FHQ::spilt(FHQ::rt,x.x+ad,a,b);

   	int kt=FHQ::kth(b,1);dot re={FHQ::xc(kt),FHQ::yc(kt)};

   	return FHQ::rt=FHQ::merge(a,b),re;

   }int check(dot a,dot b,dot c){

   	return (c.x-b.x)*(b.y-a.y)<=(b.x-a.x)*(c.y-b.y);

   }bool operator==(dot x,dot y){

   	return x.x==y.x&&x.y==y.y;

   }void solve(int abc){

   	int l=2,r=FHQ::sz(FHQ::rt);

   	db ak,bk,rk,ans=0;cin>>ak>>bk>>rk;

   	while(l<=r){

   		int mid=(l+r)/2,ida=FHQ::kth(FHQ::rt,mid);

   		int idb=FHQ::kth(FHQ::rt,mid-1);

   		db xa=FHQ::xc(ida),ya=FHQ::yc(ida);

   		db xb=FHQ::xc(idb),yb=FHQ::yc(idb);

   		if(xa*ak+ya*bk<=xb*ak+yb*bk) r=mid-1;

   		else l=mid+1,ans=xa*ak+ya*bk;

   	}if(abc!=1) mx=max({ans,fs.x*ak+fs.y*bk,mx});

   	dot x={mx*rk/(ak*rk+bk),mx/(ak*rk+bk)};

   	if(!FHQ::rt) return fs=ed=x,FHQ::insert(x.x,x.y);

   	if(fs.x>x.x||(fs.x==x.x&&fs.y<x.y)) fs=x;

   	else if(ed.x<x.x||(ed.x==x.x&&ed.y<x.y)) ed=x;

   	else if(check(pre(x),x,nxt(x,eps))) return;dot lst={0,0};

   	if(!(fs==x)) while(1){

   		dot pr=pre(x),pe;

   		if(pr==fs) break;pe=pre(pr,eps);

   		if(!check(pe,pr,x)) break;

   		FHQ::erase(pr.x,pr.y);

   	}if(!(ed==x)) while(1){

   		dot nx=nxt(x),nt;

   		if(nx==ed) break;nt=nxt(nx,eps);

   		if(!check(x,nx,nt)) break;

   		FHQ::erase(nx.x,nx.y);

   	}FHQ::insert(x.x,x.y);

   }

3.删除操作

这是凸包维护中比较困难的部分，目前遇到过两种：

  1. 线段树分治最伟大！（如 [CTSC2016] 时空旅行，适合决策单调性一类的）
  2. 多层凸包，剥完一层还有一层（如 [NOI2017] 分身术，适合计算几何题）

这种就主要看题目，灵活采用了。

二、凸壳解决决策单调性问题

这基本上是经典了。实际上，斜率优化 \(dp\) 就是用凸壳解决了 \(dp\) 的单调性问题。

基本思路是维护上/下凸壳，然后对于询问用二分找到答案。有时遇到涉及区间求值的问题，我们就可以再套一个线段树，每个线段树区间内都维护一个凸壳。特定问题中，你甚至可以使用树状数组套凸壳。至于如何建模，我将会以 [SDOI2014] 向量集一题做具体讲解。

发现题目问 \((a_i,b_i)\cdot(x,y)\) 的最大值，那么选择第 \(i\) 个向量比第 \(j\) 个向量优，当且仅当（下设 \(a_i>a_j,y>0\)）：

\[a_ix+b_iy>a_jx+b_jy \]

\[(b_i-b_j)y>-(a_i-a_j)x \]

\[\dfrac{b_i-b_j}{a_i-a_j}>-\dfrac xy \]

我们发现，假如我们将 \((a_i,b_i)\) 看作坐标系上的点，那么 \(\dfrac{b_i-b_j}{a_i-a_j}\) 相当于两点斜率：当斜率 \(>-\dfrac xy\) 时，\(a_i\) 大的更优；反之，\(a_i\) 小的更优。

这个时候，我们就会发现：假如我们建立所有点的上凸壳，那么无论任何时候，答案都在这个上凸壳上面。查询答案时，我们对上凸壳进行二分即可。当然，这都是 \(y>0\) 的情况，假如 \(y\le 0\)，那我们就需要在下凸壳上二分了。

本题有区间查询，所以可以使用线段树套凸壳的方式进行维护。本题还涉及到一个小小的 \(trick\)：当加入的点在末尾时，我们可以在一个区间被填满后再进行凸壳的建立，因为在加入最后一个点前，这个区间不可能被访问到。

综上，凸壳解决单调性问题的基本套路为：找到点的形式，判断上、下凸壳，选择数据结构。


__EOF__

 原创作者: chang-an-22-lyh 转载于: https://www.cnblogs.com/chang-an-22-lyh/p/18954850/tu_bao-zj
BZOJ 3533 Sdoi2014 向量集 线段树+凸包+三分
世界
03-17 2578
题目大意：给定一个平面，维护下列操作： 1.插入一个向量 2.询问第l到r个插入的向量中与某个向量叉积的最大值 强制在线 首先答案一定在凸包上 而且如果y>0则在上凸包上 否则就在下凸包上 且答案在同一凸包上呈现单峰函数 满足三分性质 但是现在让我们维护某个区间内的凸包，因此我们可以使用线段树 由于凸包的合并是线性的，我们不能每插入一个点都路径维护一下 这个很好办嘛！反正包含未插入
计算几何 ： 凸包学习笔记 --- Graham 扫描法
北岛知寒
03-05 488
凸包 (只针对二维平面内的凸包) 一、定义 简单的说,在一个二维平面内有n个点的集合S，现在要你选择一个点集C，C中的点构成一个凸多边形G，使得S集合的所有点要么在G内，要么在G上，并且保证这个凸多边形的面积最小，我们要求的就是这个C集合。 二、算法 求凸包的算法很多，常用的有两种： 1.  Graham扫描法，运行时间为O(nlgn)。 2.  Jarvis步进法，运行时间为O
【斜率优化】凸包维护
10-04 274
总结一下凸包维护规律: 斜率为负,从小到大,维护U左半部分凸包,求最小y截距 斜率为负,从大到小,维护倒U右半部分凸包,求最大y截距 斜率为正,从小到大,维护U右半部分凸包,求最小y截距 斜率为正,从大到小,维护倒U左半部分凸包,求最大y截距 转载于:https://www.cnblogs.com/Rojo/p/4695628.html...
凸包问题--动态凸包（平衡树维护）
永远鲜红の幼月的博客
03-06 3980
前景提要： 继承上一张学习的凸包问题，下面我么来总结一下动态凸包的维护问题。 一些点已经构成了一个凸包之后，新加入||删除一些新的点的时候，会对原有的凸包产生一些影响，如果每次都重新把所有点都重新计算一遍凸包的话，那将非常耗费时间，以至于必定会WA，因此，我们就学习动态凸包的维护方法。 目录 前景提要： 观察总结凸包的维护 平衡树的维护 CF-70D-D. Professor's t...
维护凸包之前的误区
幽灵悠悠
04-21 227
02 说人傻就要多总结！ 昨天学习了x递增的时候凸包的该怎杨维护，当x不递增的时候好像需要归并算法，或者是平衡树，应该是不简单的。 首先要维护一组斜率上升的一组点，这样维护的凸包可以找到截距的最小值，我之前还在想当斜率为负数的时候该怎么办，其实在维护凸包的过程中已经维护了当斜率为负数的条件下造成截距最小值的点，这样大概的形状是一个放在桌子上的碗。 维护的过程就是维护一个斜率单调上升的点，如果前凸包...
BZOJ 2300 防线修建（set维护凸包）
weixin_34302798的博客
01-08 173
题目链接：http://61.187.179.132/JudgeOnline/problem.php?id=2300 题意：给出一些点，两种操作：（1）删掉某个点；（2）求剩下点构成的凸包的周长。（保证凸包有一条边为x轴，即保证凸包上有两点在x轴上，这条边不算在周长中） 思路：离线。先将所有删掉的点删掉，其余点找到一个中心点（由题意其余点至少三个所以中心点存在），求每个点关于中心角的转角，以转...
计算几何基础凸包学习笔记
12-25
计算几何基础凸包学习笔记
计算几何凸包进阶学习笔记
12-25
计算几何凸包进阶学习笔记
4. 凸包算法（学习笔记）
最新发布
springvil的博客
04-11 1190
平面的一个子集S被称为是"凸"的，当且仅当对于任意两点pq∈Sp,q\in Spq∈S线段pq都完全属于S。集合S的凸包Conv(S)，就是包含S的最小凸集。这里所要讨论的，是如何计算平面上由n个点组成的有限集合P的凸包。可以借助一个虚构式实验，来想像这种凸包的模样：将这里的点想像成钉在平面上的钉子；取来一根橡皮绳，将它撑开围住所有的钉子，然后松开手——啪的一声，橡皮绳将紧绷到钉子上，它的总长度也将达到最小。此时，由橡皮绳围住的区域就是P的凸包。
点云学习笔记17——PCL提取保存到的二维点云边界（即凸包边界）
qq_64095888的博客
11-14 558
【代码】点云学习笔记16——PCL保存提取到的二维点云边界（即凸包边界）
牛客网多校2 message（凸包维护）
XFire的博客
08-09 311
题目：给你n条直线的y=ax+by=ax+b中的aa和bb，和m次查询，每次查询给要求的直线的y=cx+dy=cx+d,中的cc和dd，要求出这条直线与n条直线交点中，x最大的值，且x大于0，如果不存在输出No cross.(n&lt;=5e4,m&lt;=5e4) 思路：交点x= - (b-d)/(a-c) 可以看作是两个点(a,b),(c,d)斜率的相反数。将之前输入的直线的斜率和截距看作一...
bzoj-1492 货币兑换Cash (1)——平衡树维护凸包
140142
07-11 2035
题意： 有n天和m的初始金钱，用来购买AB两种纪念券； n天里每天都有AB的价格，每天可以进行这样的操作； 1.卖出手中x%的纪念券(AB分别都卖出x%)； 2.用x的金钱买入纪念券，买入AB券的比例在第i天为Rate i； 求n天过去之后所获得的最大收益； 金钱和券数均为实数； n 题解： 首先，虽然题中的买入和卖出都是任意数量的，但是同样的纪念券，分几天卖出得到的收
[CodeForces - 678F] Lena and Queries 线段树维护凸包
weixin_30794491的博客
07-27 361
　　　大致题意： 　　　　　　给出三种操作 　　　　　　　　1、往平面点集中添加一个点 　　　　　　　　2、删除第i次添加的点 　　　　　　　　3、给出一个q，询问平面点集中的q*x+y的最大值 　　 　　　　首先对于每个询问，可将z=q*x+y转化为y=z-q*x，即过点（x，y）的斜率为-q的最大截距，很容易发现这些点只会在上凸包上，只要在 　　　　凸包上三分即可。 　　　　对...
bzoj 4515 [Sdoi2016]游戏 线段树维护凸包
make_it_for_good的博客
10-27 516
先树链剖分转成区间问题。 S到T的路径可以拆成S-lca和lca-T。 设d[r]表示根到r的距离。 对于S-lca中的点r，加的值为： a∗(d[s]−d[r])+b=(−a)∗d[r]+(a∗d[s]+b)a*(d[s]-d[r])+b=(-a)*d[r]+(a*d[s]+b) 对于lca-T中的点r，加的值为： a∗(d[r]+d[s]−2d[lca])+b=a∗d[r]+(a∗d
BZOJ 3533 [SDOI2014]向量集 (线段树维护凸包)
weixin_30413739的博客
02-10 173
题面：BZOJ传送门 洛谷传送门 容易想到这样一个结论 把每次插入向量$(z,w)$改为在坐标系内插入一个点$(z,w)$，并对这些点建出凸包。 每次询问向量$(x,y)$的答案，设一条直线$l$垂直于$(x,y)$，用l去切所有已知向量构成的凸包，第一个切到的点就是最优解，根据$y$的正负来决定是从上面切还是下面切 简单证明一下，向量点积相当于向量$(z,w)$在$(x,y)$上的投影*...
BZOJ 5039: [Jsoi2014]序列维护 线段树
BlackJack
09-05 809
5039: [Jsoi2014]序列维护 Time Limit: 20 Sec  Memory Limit: 256 MB Submit: 56  Solved: 39 [Submit][Status][Discuss] Description JYY 有一个维护数列的任务。 他希望你能够来帮助他完成。 JYY 现在有一个长度为 N 的序列 a1,a2,…,aN，有如下三种操作：
利用线段树维护凸壳（李超树）
Never give in.
04-01 1490
Text之前听lyd_729神犇讲过关于李超树的思想，大概是标记永久化一类的要求支持动态插入直线（线段），动态查询上/下凸壳与x=k的交点，k为整数 今天做模拟赛的时候刚好碰到一题，然而忘得差不多了 考场上自己YY了一个：线段树每一个区间都保存一条直线，表示在这个区间中这条直线有可能有一部分为凸壳中的边当我们需要插入一条直线（线段），与当前线段树区间保存的直线进行比较，看哪一个斜率大，哪一个更优
CF 678F Lena and Queries 线段树维护凸包+三分
weixin_43824564的博客
07-31 285
题意：维护一个点集 向点集中进行插入删除和查询的操作 其中查询操作是 求 q*x+y的最大值 设 z=q*x+y 得到y=-q*x+z 显然我们需要使得截距z最大 我们需要维护一个凸包 然后在通过三分在凸包上找到最大值 不过显然我们不能每次询问都去求一个凸包 那样复杂度是无法接受的 我们可以维护每个点出现的时间 然后把它挂在线段树上面 最后在遍历一遍线段树就行了 （类似于线段树分治的思想） #include<bits/stdc++.h> using na...
OpenCV3编程学习笔记及实例代码解析
资源摘要信息:"OpenCV3学习笔记+自己整理的程序小代码.zip文件包含了关于OpenCV3图像处理库的学习笔记以及一些编程练习的代码文件。OpenCV是一个开源的计算机视觉和机器学习软件库，它提供了大量的图像处理功能以及...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值