c++ 修改向量某位置的值_平面向量笔记

这是高考完的第一篇文章，以后打算发一些自己高中的笔记和自我学习研究成果，这次先来点平面向量（高中笔记）

一 . 等值线（和，差，商，积）

二 . 三角形四心与奔驰定理

三 . 极化恒等式及其变形推论

首先来说说等值线（和，差，商，积) :

说明：平面向量基本定理：如果

是同一平面内的两个不共线的向量 ，那么对于这个平面内的任一 向量

，有且仅有 一对实数

，使

，我们称

为平面向量基本定理系数 ．

1.等和线：我们都知道，在平面向量中，如果有

的话， 若P在直线AB上，则有

，本来这么简单就不想证明了，但考虑到其中有一个知识点，就证明一下吧

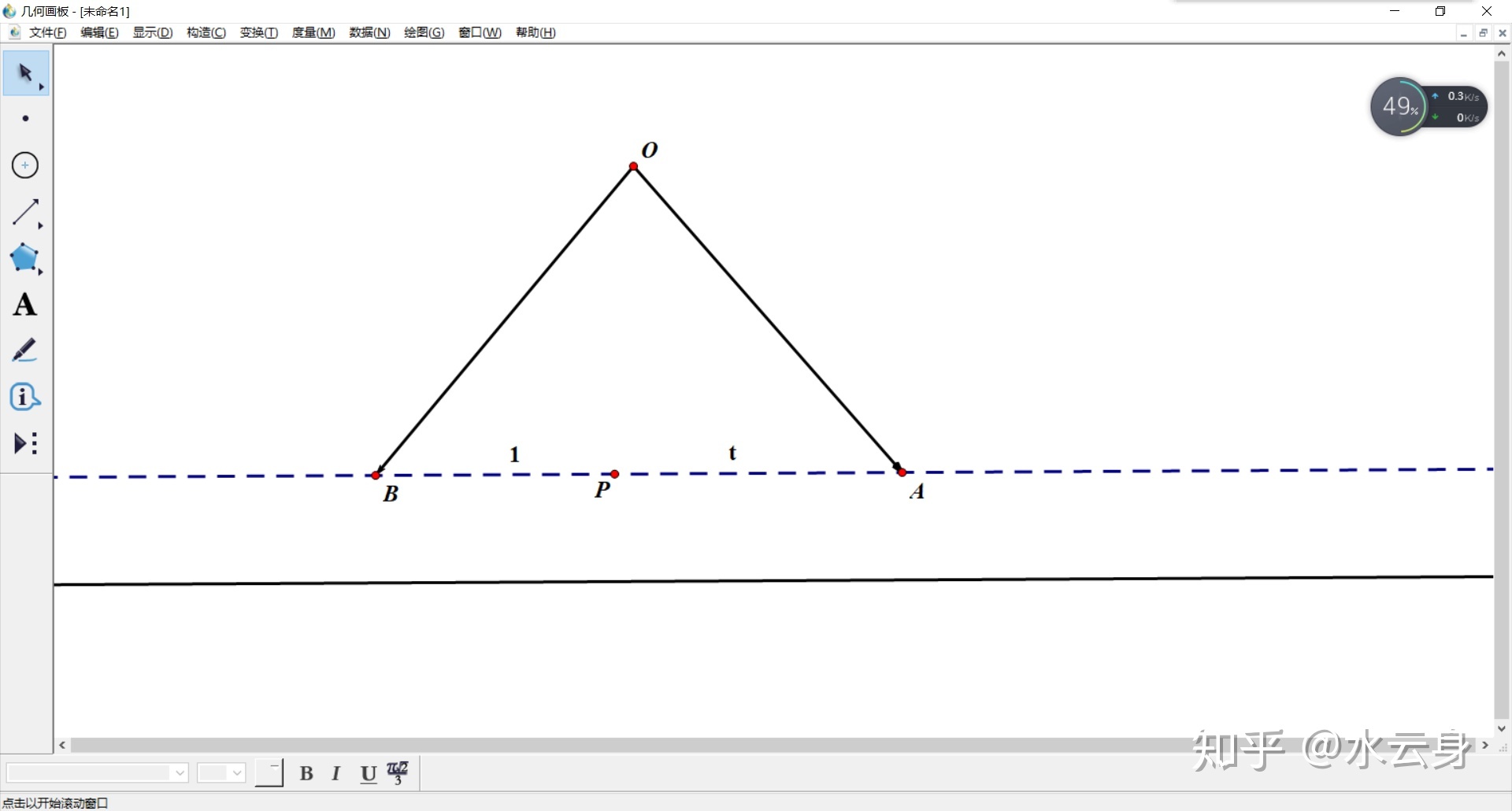
证明：不妨设

∴

, 即

∴

∴

你可能会注意到：

，刚刚好就是交叉系数

具体不多讲，自己悟吧，接着等和线

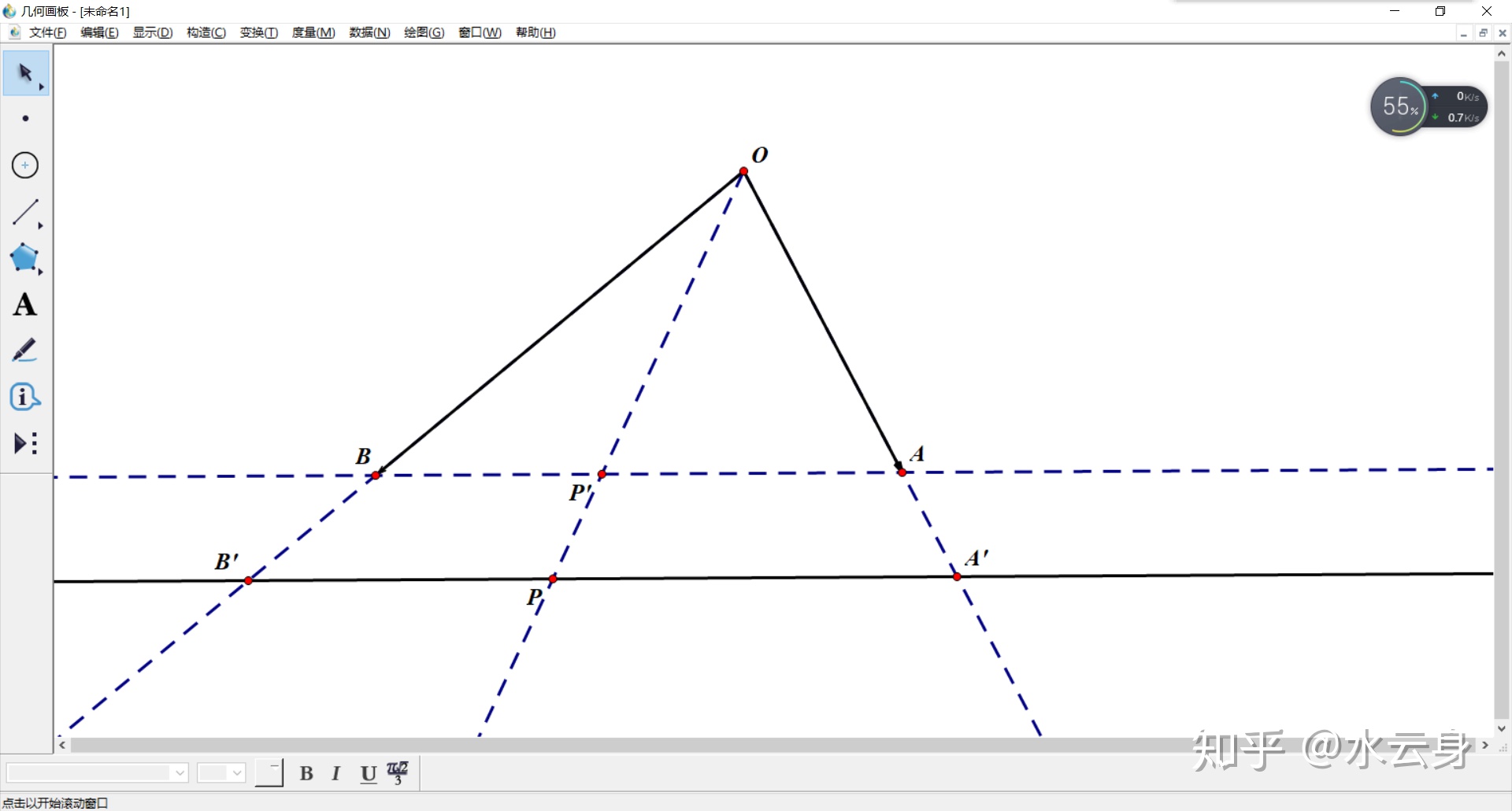
刚才P点是在直线AB上的，那如果P点不在直线AB上呢？比如下图

,

不妨设

（

),

那么 x+y=1

但是现在

, 求

，怎么办呢，跟x+y和k又有什么关系呢

下面用代数的方法探讨一下

点P’没标出

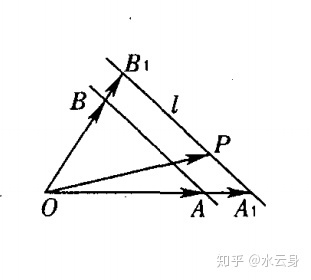
如图，

即：

， 显然k只与直线AB与直线L的相对位置有关，而与P点在L上的位置无关，

所以，对于平行与直线AB的直线上的任意一点P，以

为基底的向量

的平面向量基本定理的系数和为定值．

反之，对于任意两个向量

, 若有

且

,移项得：

∴

从而：

于是有：平面内一组基底

,及任一向量

，

点P在直线AB上或在平行于AB 的直线上 ，则

(定 值 )，反之也成立 ．

我们 把 直线 AB 以及与 AB平行的直线叫平面向量基本定理系数的等和线

代数法比较严谨，也略显麻烦，下面这个方法比较容易理解

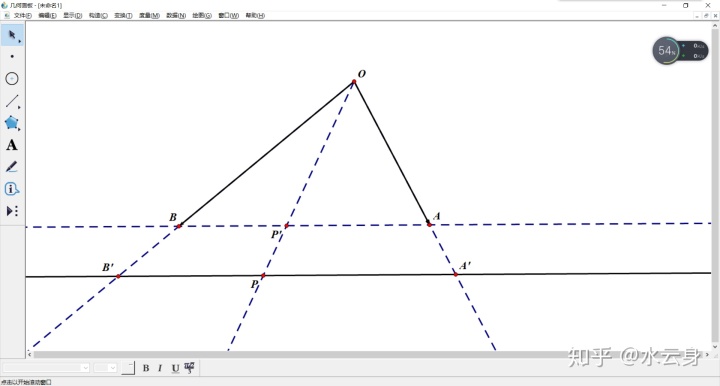
如图，

， ∵ A,B,P'三点共线，∴x+y=k

等差线：简单的来说就是平行三角形ABC的AB边中线的直线,若P点在该直线上，那么

（定值）

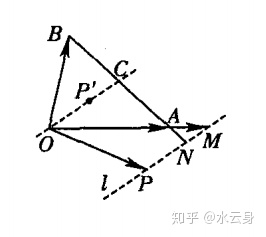
平面内一组基底

，C为线段 AB的中点，

，设P'为直线OC上任意一点，则

,

此时

，

不懂？看看下面这图

,

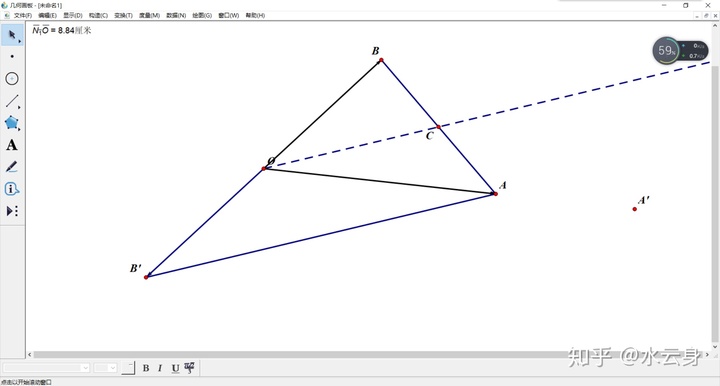
这下就简单易懂了，繁杂的代数就不写了，参考上面

等商线：若点P在过O点的直线上（非O点），以

为基底的向量

的平面向量基本定理的系数和为定值．即

（定值）

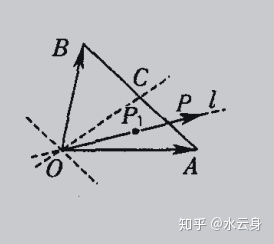
下面证明充分性（必要性就不证了，懒）：

设

，

,且P,P'都在直线L上

则

，

∴

若以O为原点，OA,OB,分别为x轴和y轴，那么k就是该直线的斜率（这就涉及到开头那个小知识点了）

到最有趣的等积线：平面内以

为基底的向量

，若

，

且

（定值），则P点在以直线 OA，OB为渐近线的某条双曲线上；反之，

点 P在以直线 OA，OB为渐近线的某条双曲线上，

则

为定值．我们把以直线 OA，OB 为渐近线 的双曲线叫平面向量基本定理系数的等积线

与上面三个不同，他们都是直线，而这里的等积线是双曲线

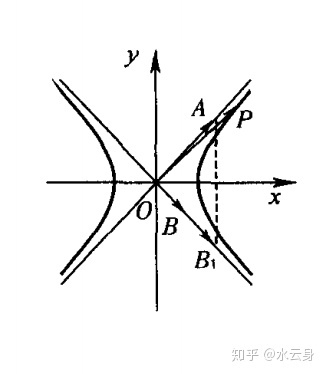
以 0 为原点，∠AOB平分线所在直线为x轴 ，建立直角坐标系 ，设

，若点 A 关于x轴对称点为B‘，则

且

那么 ：

∴

那么

相乘得：

(1)当双曲线有一支在∠AOB 内时，

为正值 ；

(2)当双曲线都不在∠AOB内时，

为负值 ；

(3)特别地，

时，

点 P 在双曲线

上，此时

=

至此，平面向量等值线搞定了

二 . 三角形四心与奔驰定理

奔驰定理应该很多人知道，网上证法也是一大堆，这里有一个巧妙的证法

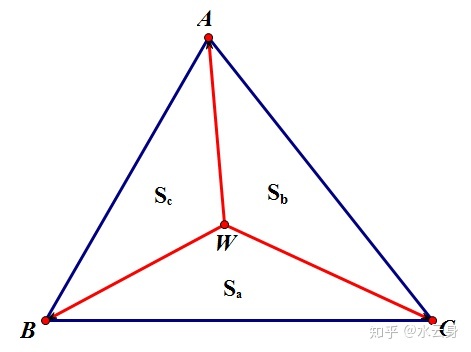
奔驰定理 ：

我们先证明一个引理。

引理：空间中任意四点W、A、B、C共面的充要条件为：

，

其中O为空间内任意一点。

证明：

∵

∴

∴

∴ W、A、B、C四点共面（共面向量基本定理）

由于O是任意一点，故取O点就为W点，那么就可以得到下面的四点共面基本定理：

空间四点W、A、B、C共面

1. 进一步可以证明，如果点W位于直线AB上，则z=0，W位于直线BC上，则x=0，W位于直线AC上，则y=0。
2. 如果W是
   内部的点，则
   ，
   ，
   。
3. 如果W是
   外部的点，当W与A在BC的两侧，则
   ，当W与B在AC的两侧，则
   ，当W与C在AB的两侧，则
   。

由于

，因而我们可以取

，

，

，于是：

，

即：

记为 三角形内点向量式。
采用解析几何的表达方式，设

，

，

，

，则有：

，

。

1.重心G
由于重心分中线长之比为2:1，则有

，于是重心坐标为：

2.内心I
由于

，

，

，

，则有内心坐标为：

3.外心O
由于

，

，

，

，则有外心坐标为：

4.旁心P
以c一边的旁心为例，

，

，

，因为c边旁切圆圆心在三角形c边一侧的外面，因而

取负值，所以旁心坐标为：

以上奔驰定理笔记摘自：三横先生链接：https://zhuanlan.zhihu.com/p/25877014

四心常见的表达式：

,则O为重心

或者

.则O为垂心

,则O为外心

，则O为内心

举个例子：在▲ABC中，cosA=

，

，

，

求x+y的最大值。

通解就不写了, 做个图

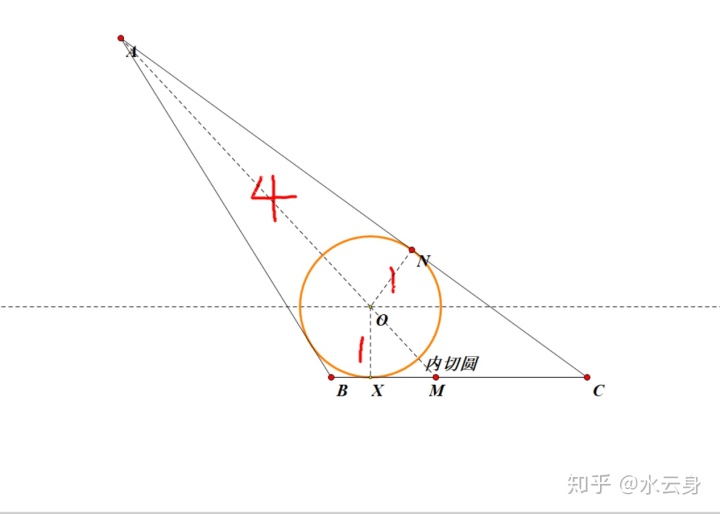
易得：cos∠OAN=

, 不妨设ON=OX=1,则AO=4

∴

，当且仅当AB=AC时，等号成立

其实奔驰定理中还隐藏着等值线

看出来了吗？

三 . 极化恒等式及其变形推论

首先是极化恒等式：

化简就是：

至于这个有什么用呢，能被这条式子解决的问题多如牛毛，举个例子

但有些题目不会这么简单就问你

等于多少，可能变着法来问，比如

那么极化恒等式就可以变一下形：

，这是其中一个简单的变形

还有:

,

这个变形就推导出中线长公式.

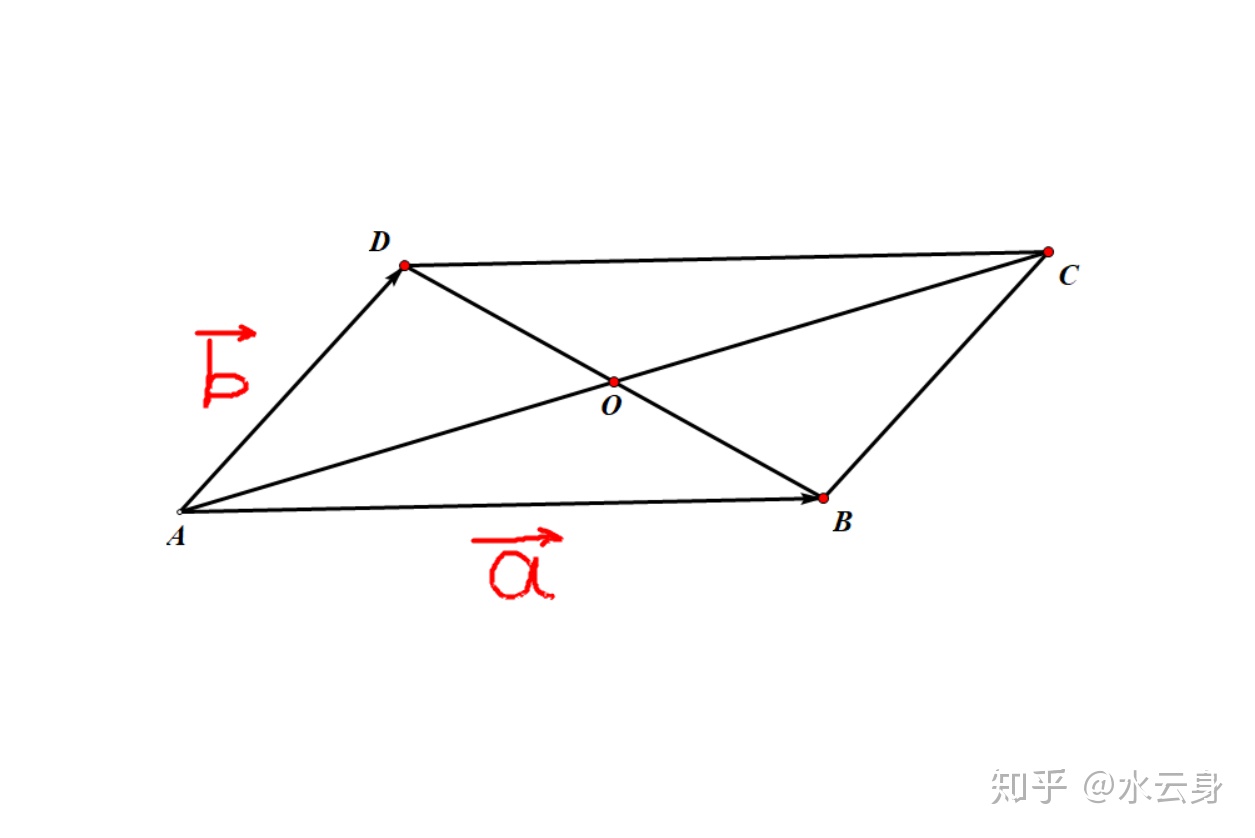
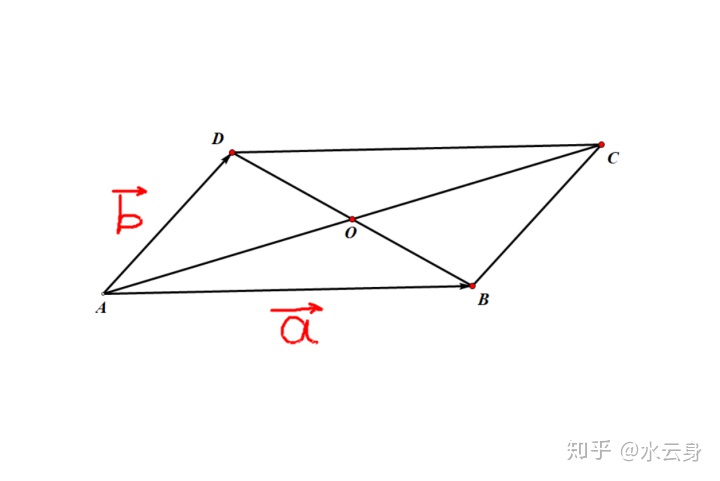
那么由此我们可以得出，在平行四边形ABCD平面内存在一点P，有：

若平行四边形ABCD为矩形，则有：

这里写一条例题吧，题目大意：

，

求

最值。

代数比较麻烦，不妨用几何法，先画个图

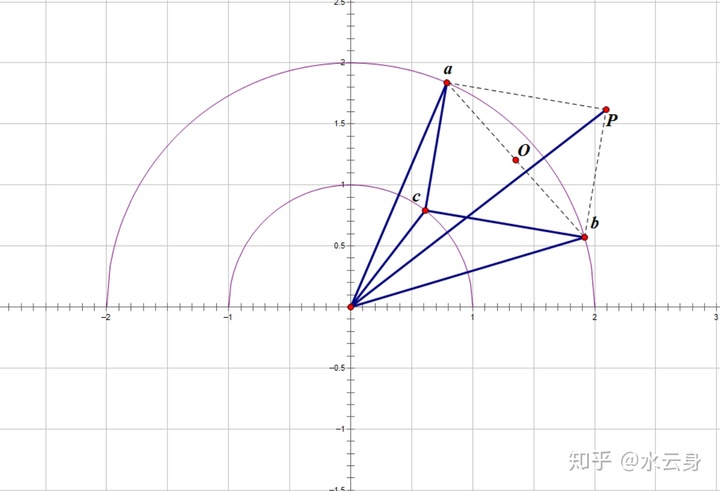
易得：

又∵

同理：

综上：

还有余弦定理的变形：

,这个式子单独没什么用，不过拿它来证明下面的式子，就好用了

,

证明：

这个式子不仅可以用来算四边形对角线夹角的余弦值，更强大的是能算两异面直线夹角的余弦值，也就是三棱锥对边夹角的余弦值

懒得打字。。。

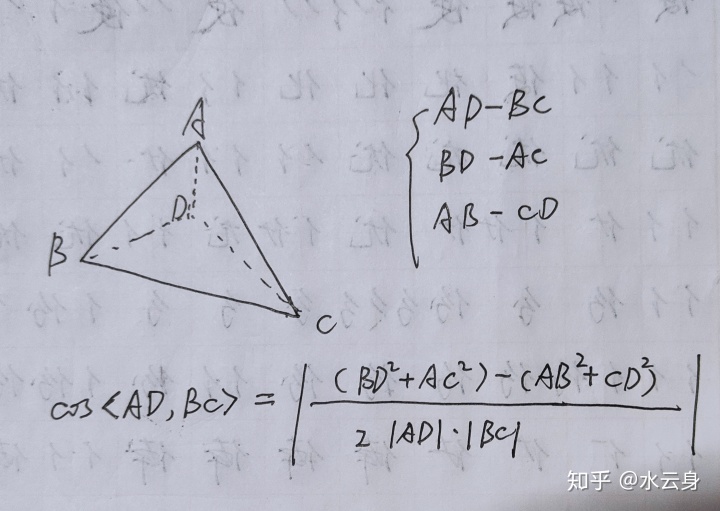
证法同上，也不难

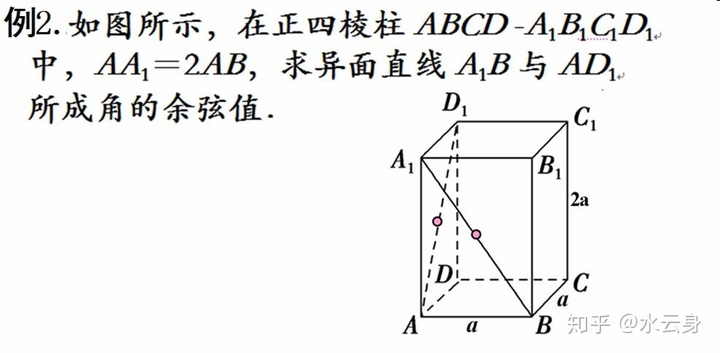
这种题直接做就完了

，特别的，当AC⊥BD时，

, 这不禁让我想起托勒密定理和婆罗摩笈多定理。