matlab线性平面映射求通项_MP8：局部线性化：从Taylor展开到微分形式

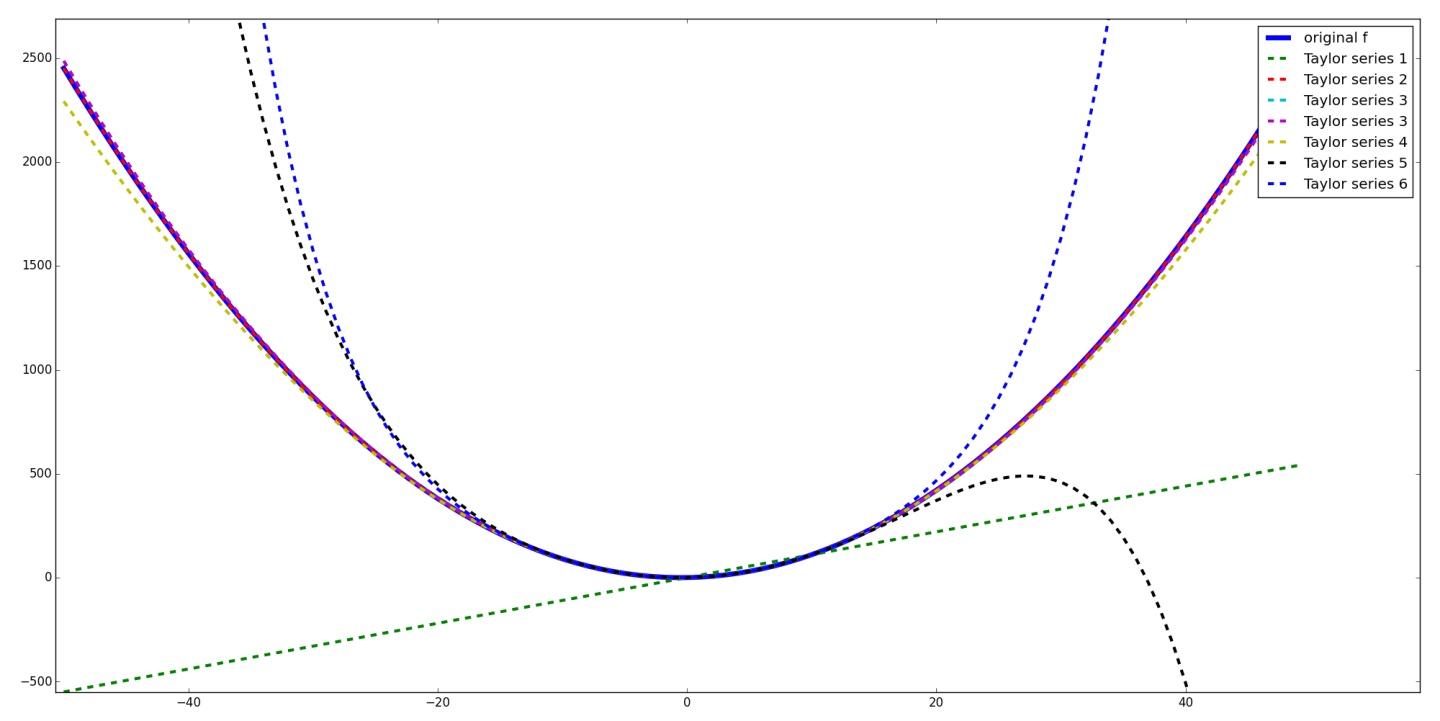
本讲回顾了高等数学/数学分析中经典的Taylor展开技术。我们关注的是Taylor展开的线性部分，这部分的线性系数就是函数的导数。在多元函数中，这部分的一组线性系数构成了某种线性组合。

站在线性代数的角度看待Taylor展开的线性部分，我们考虑两个问题：

坐标的微分能否构成某种线性空间的向量？

坐标的微分能否构成这个线性空间的基？

我们研究了坐标分量函数，这类函数的微分就是坐标的微分，几何上它们构成了一组正交的超平面系。借助这类函数，我们发展出了微分形式的概念，确认了以上两个问题，即坐标的微分就是对偶空间的向量，坐标的微分正是这个线性对偶空间的基。

之后我们研究了这类微分形式的几何意义，通过它们线性组合，可以构成具有任意梯度的微分形式。

广告：高中生想快速学会微积分、线性代数，尝试大学数学物理知识戳这里网上私教 学霸养成。

---

上一讲中，我们在考虑如何把

上的向量场推广到一般的光滑流形

时，遇到了一些问题。这些问题反映出流形和平直空间内在的不同。这些问题的解决需要等到完全理解

切空间/余切空间的概念。在展开讲解之前，在这一讲中我们先谈谈局部线性化的思想，同时储备一些技术工具。

回顾微分流形

的定义，其中提到

都

：

使得开邻域

和

中的开集同胚。

这使我们注意到：

1. 这里是逐点定义的，且只考虑每一点的某个邻域的存在性。这提示我们采用了局部的方法。
2. 局部（开邻域）和
   中的开集同胚，意味着在局部试图接近
   这样的平直空间，所谓平直，就是
   线性，实际上
   中嵌入的平直空间（直线、平面、超平面）就称为
   线性流形。

这些思路，我们总结为局部线性化。局部线性化的思想贯穿于微分几何的研究中，这也是我们一直强调同学们学好线性代数的原因（另一个思想是借助拓扑学的整体微分几何）。这一讲中，我们详细谈一下如何借助古老的Taylor展开技术，把局部线性化的方法发展为微分形式。

Taylor展开

微积分中我们熟知Taylor展开，在一维的情况，函数

在点

附近可以写为幂级数和的形式：

注意到

次项

是常数项，而当

求极限时：

在

处求导将消去

次以上高阶无穷小量，只剩下

次的线性项，得到我们熟知的关系：

站在我们现在的角度看，Taylor展开就是一种函数逼近技术，当考察固定点

附近的局部（邻域）时，成为了一种

线性化的，只保留一次导数

的逼近。

注意到Taylor展开的局部线性化也可以表示成：

这一方面反映了导数的局部线性的性质，另一方面，导数

在固定点上是常数，它本身可以视为

线性系数。在

维看得更加清楚。

维函数

在点

附近的Taylor展开，进行局部线性化后得到：

这里用了Einstein求和约定。显然，偏导数

起到了

线性系数的作用。现在我们得到了某种类似 线性组合的关系。然而，若要放心地用线性代数的方法来处理，我们首先需要明确两个问题：

1. 和
   是否是某个向量空间中的向量？
2. 如果是，
   能否构成基？

如果我们能够解决这两个问题，过去我们所理解的所谓无穷小量的微分将被赋予线性空间的新的内涵，它是将来要讨论的余切向量的原形。

超平面系

在

中，记自然基为

。考虑一组特殊的函数

分量函数

，其中每一个表现为：

即把点

的第

个分量

输出为函数值。

注意：指标

在上面表示它是

函数：

指标在下面表示它是坐标 分量：

分量函数

对分量

求偏导数：

这里用了Kronecker记号。于是仅在指标

时有意义：

即

上式中，左边的指标

在上面表示函数的微分，右边的指标在下面表示自变量的微分。我们理解为，

函数微分和 自变量微分可以等同看待。

由分量函数的函数微分和自变量微分的等同关系可见，分量函数

的几何意义是，每一个函数

都是线性函数，它构成一个

超平面（线性流形），这组超平面相互 正交。

1-微分形式

将

维实线性函数所构成的空间记为

。这个线性函数空间蕴含了自然的线性运算，即

：

我们注意到上面讨论的分量函数

中的每个函数都是

维实线性函数。前面谈到它们构成了正交的超平面，代数上意味着

是函数空间

中的

线性无关子集。

现在考虑某一点

附近的线性函数空间

。如前面的讨论，任意函数

在点

附近若可微，则可以通过Taylor展开，在

附近消去高阶无穷小量后，局部视为一个线性函数

：

更重要的，可以把这个线性函数

表达为点

附近分量函数

的线性组合：

对它求全微分：

这里的

是线性系数。这里出现的

既可以视为变量

的微分，也可以视为函数

的微分。

非常重要！回到前面我们提出的问题：

1. 和
   是否是某个向量空间中的向量？
2. 如果是，
   能否构成基？

现在，在某一点

附近，由于

被局部线性化，

和

的成员都是

中的元素。我们把微分算子

视为从

线性函数空间到 函数微分集合的映射：

由于微分的线性性，自然可以在函数微分集合

中构建线性运算，构成线性的

函数微分空间。于是，

和

是函数微分线性空间

中的向量。

其次，由于

是一个线性无关的集合，可以证明微分算子

将它映射成函数微分线性空间

中的基

。

最后，根据全微分公式：

即：任意函数

在点

附近若可微，则可以通过Taylor展开在

附近进行局部线性化，得到函数微分

，它是基

的线性组合。

这个函数微分线性空间

中的元素称为

1-微分形式(differential form)，简称 1-形式。本质上，1-形式相当于局部（在相差一个常数的意义下等价，后面详述）线性函数。

1-形式的几何直观

函数

的几何意义是，在点

附近，每一个函数

都是

中的线性函数，它构成一个

超平面（线性流形），这组超平面相互 正交。

微分算子

将这组线性函数映射成函数微分，即：

注意这种映射不是单射，若有任意实数

则：

即，相差为常数的线性函数具有相同的函数微分，相同的函数微分对应着等价类。由于任意线性函数也是

的线性组合，这种等价关系对于任意函数微分

都成立。于是满足微分为

的线性函数是一个集合，这个集合中的线性函数两两之间相差一个常数。几何上看，

决定了一组平行的（相差常数）超平面（线性函数）。

作为1-形式，

体现了基

的线性组合，几何上看，每一个基向量（1-微分形式）都代表一组平行超平面，基向量之间相互正交，通过系数（偏导数

）组合，构成了具有任意

梯度的一组平行超平面。