函数平移口诀_初中数学--函数平移为什么是左加右减，上加下减

在初中数学学习过程中，不少同学应该背诵过函数平移的口诀：左加右减，上加下减。

假如不加思考的背诵这个口诀，那其实也能应付大部分情况。

但假如想要思考下口诀的来源，开始可能只有困惑。

比如，对于平面坐标系，右侧是x轴正方向，上侧是y轴正方向。第一印象，两者应该同时加或者减，而结论却是一加一减。

下面我以二次函数

为例（因为二次函数有顶点坐标，看的更加清楚）

开始位置，毫无疑问，顶点

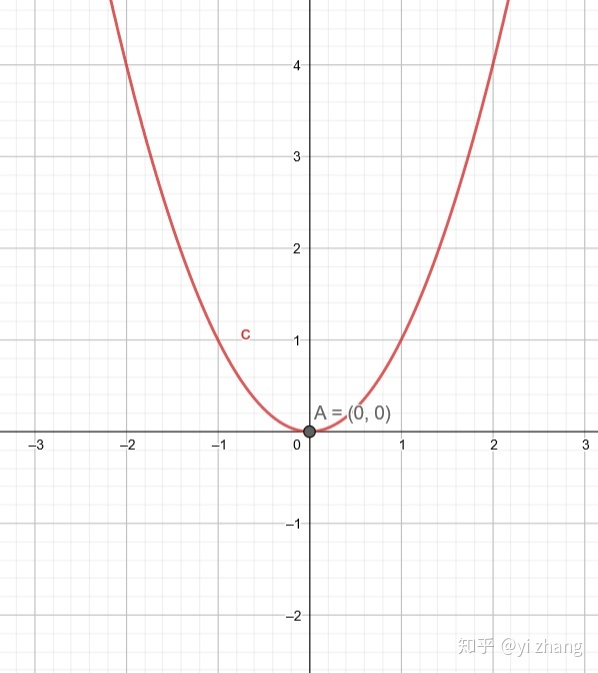
我将其向上移动两个单位得到

顶点变成

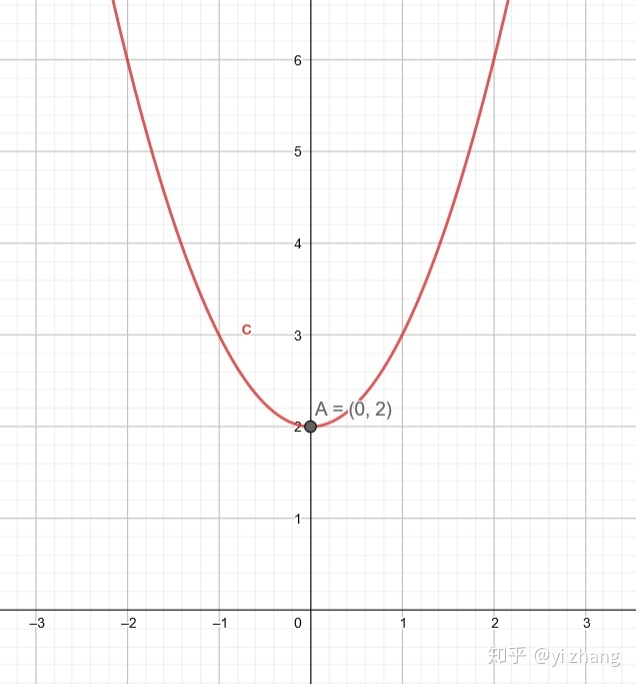
在将函数图形向右平移3个单位得到

顶点变成

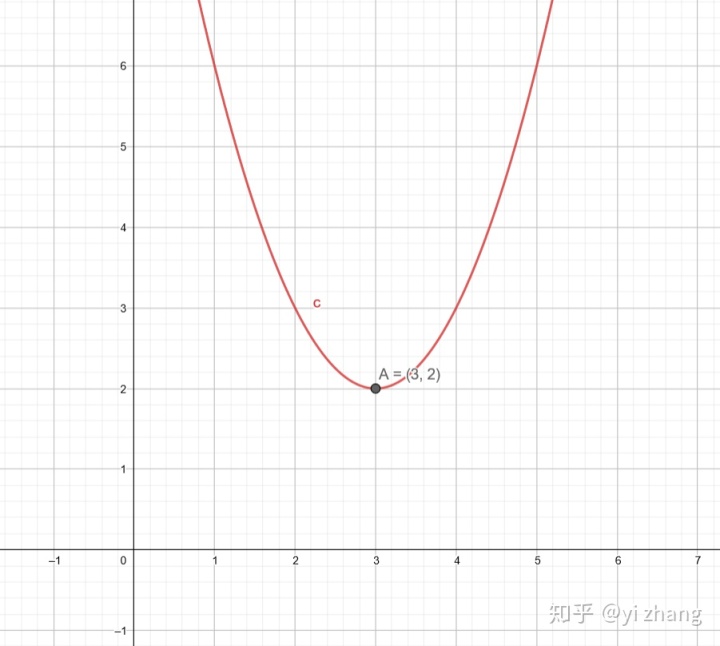
这时候，似乎矛盾的结论出现了。

将函数向上平移两个单位，向右平移三个单位后。

对于函数，分别是-3，和+2。

但是顶点坐标却忠实的+3和+2.

---

似乎顶点坐标是一个乖宝宝，和我们开始设想的往x轴和y轴正方向平移后数值会增加。

但函数本身却似乎不是。。。

回到开头，往x轴平移是x那边有变化，也就是等号右边有变化。

那么往y轴平移为什么也是等号右边的变化，假如我们把变化量放到左边会有什么不同。

我们移动常数项2的位置

那么原来的

会变成

似乎我们找到了答案。

往x轴正方向平移，对于x的分量是减，也就是左加右减。

往y轴正方向平移，对于y的分量是减，也就是下加上减。

但这个有和顶点坐标的变化是相反的。

如何理解呢，对于坐标上的点，往右和往上，是毫无疑问的会是坐标数值增加。

而为了补偿这个增加，函数本身需要扣除相应的增加量。

而这里面函数上的点不局限于顶点，函数也不局限于二次函数。

如下图，二次函数上另一点B（0，2）也随函数整体平移而平移。

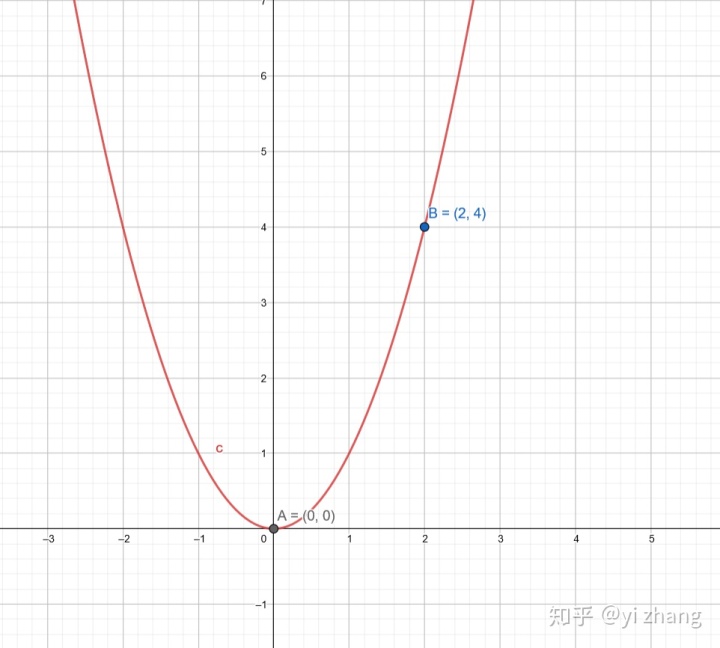
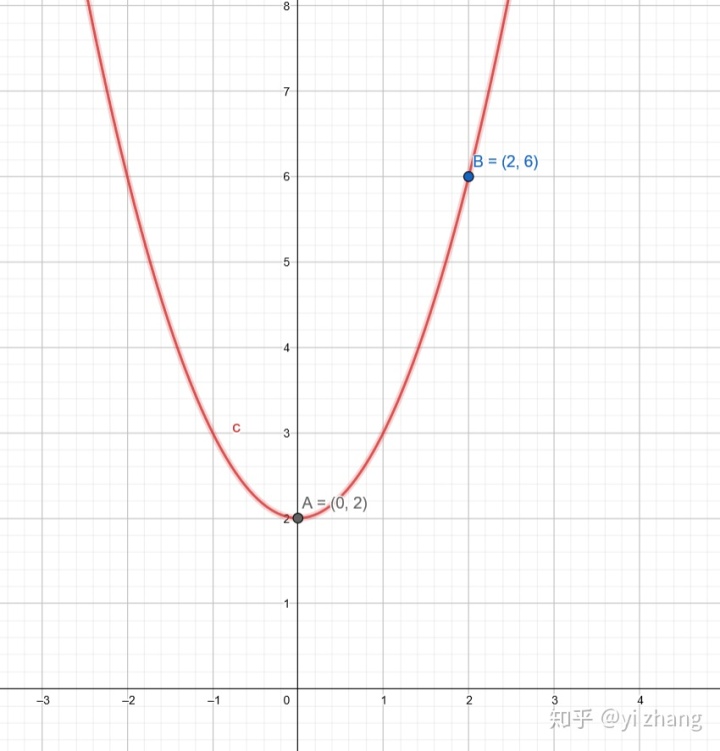
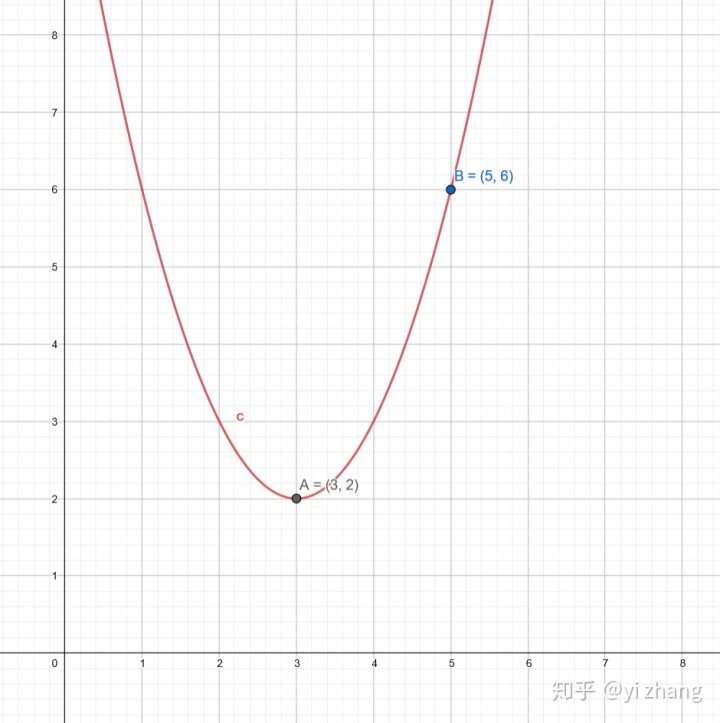
如图，对于函数

有ABCD四个顶点。

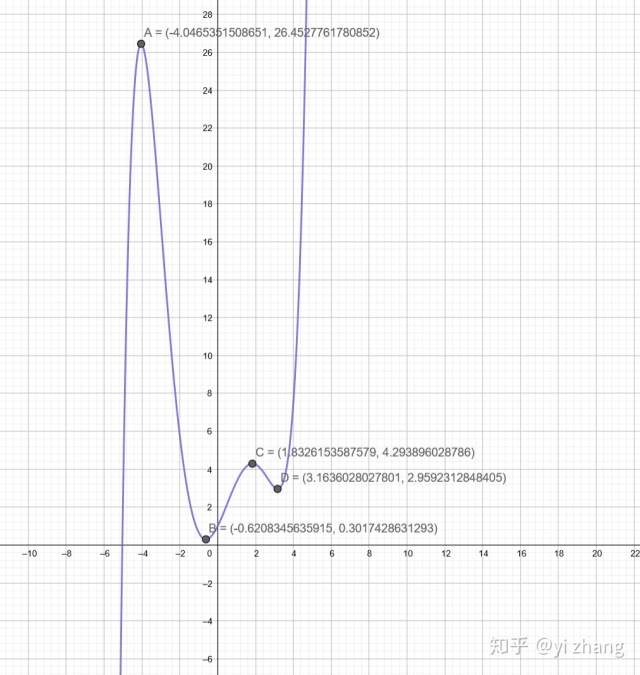
向右平移5个单位

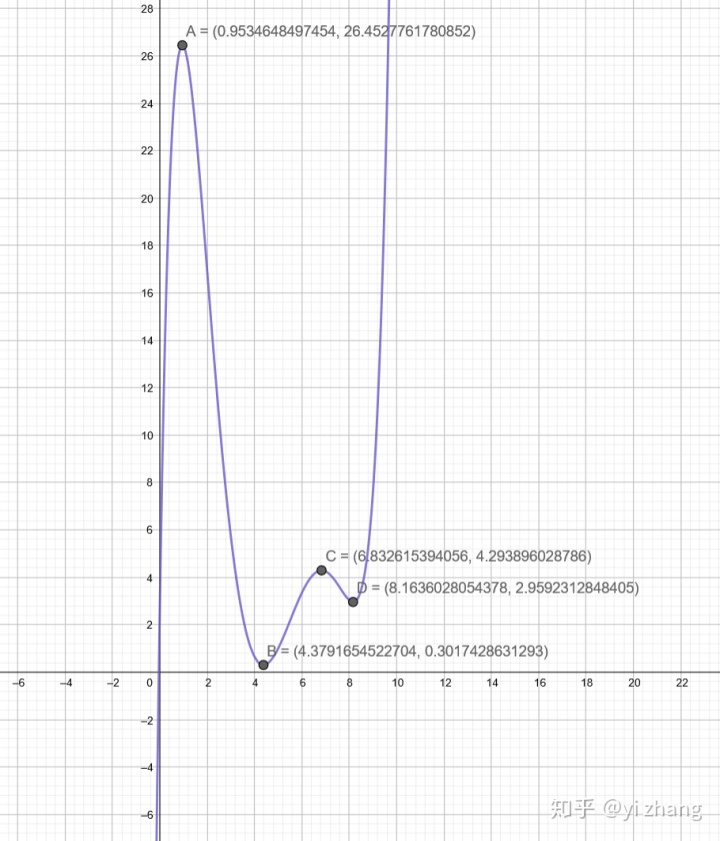
向下平移7个单位。

结果和我们猜测的结论一致，上面点坐标平移，含有这些点的函数本身需要补偿这些变化，需要在反方向改变。