相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。
相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。
但是,请记住,相关性不等于因果性
两个重要的要素
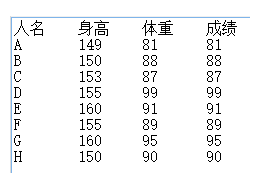
从非常直观的分析思路来说,比如分析身高和体重,我们会问个问题:.身高越高,体重是不是越重?问题细分为两个方向:1,身高越高,体重越重还是越轻。2,身高每增加 1 ,体重又是增加多少或减少多少。這就是相关性的两个重要要素:相关的方向和相关的强度。对于相关的方向很好理解,就是正相关、负相关还是无关。对于问题2,有不同的人产生了不同的 定义相关性强度的思想。
皮尔逊相关系数
皮尔逊相关系数全称为:皮尔逊积矩相关系数(Pearson product-moment correlation coefficient).该系数广泛用于度量两个变量之间的相关程度。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来.定义的公式如下:
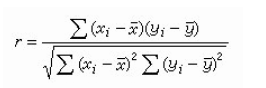








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 620
620











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








