MATLAB仿真同步电机模型实践指南

本文还有配套的精品资源，点击获取

简介：同步电机在电力系统和工业领域有着广泛的应用。本文介绍了使用MATLAB及其SIMULINK环境进行同步电机建模和仿真的关键步骤和概念，包括电机的基本结构、数学模型、控制策略、仿真参数设置、结果分析、优化设计及验证。通过这些实践指南，读者可以深入理解同步电机的工作原理和性能，并优化电机设计。提供资料包含MATLAB代码、SIMULINK模型和文档，以辅助学习和研究。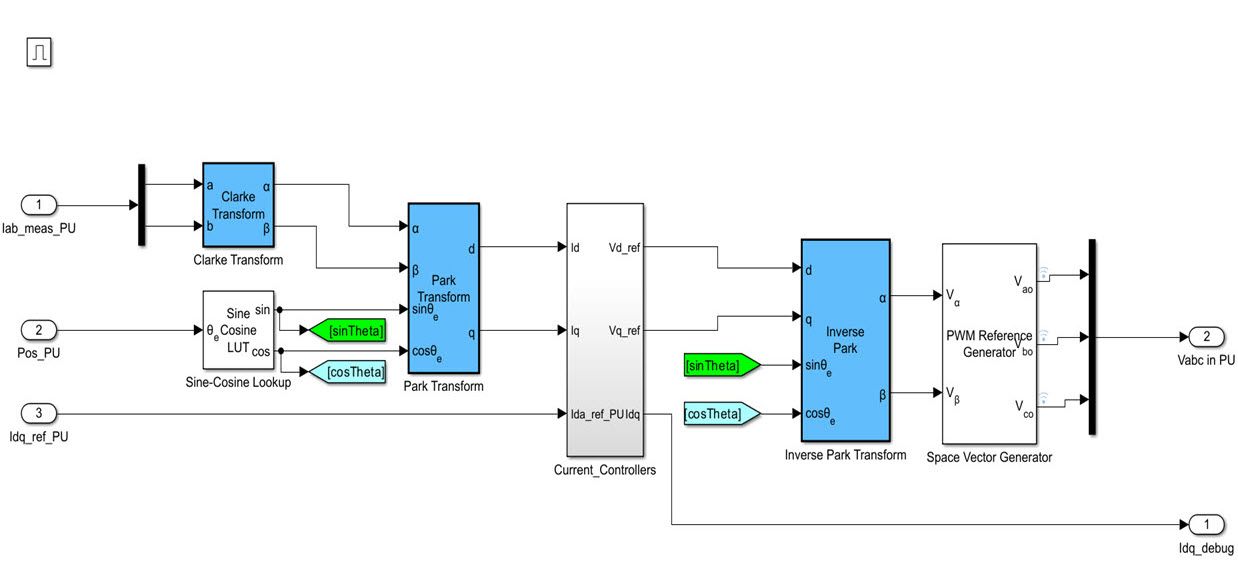

1. 同步电机基本概念

1.1 同步电机的定义与特征

同步电机是一种交流电机，其转速与电源频率保持同步。这类电机广泛应用于电力系统中，因其能够提供无功功率和调节系统电压而备受重视。它们的核心特征是转子磁场与旋转磁场以相同的频率同步旋转。

1.2 同步电机的工作原理

从工作原理上讲，同步电机依赖于交流电源供电，通过电磁感应产生旋转磁场，并驱动转子以固定的速度旋转。这主要依赖于转子中直流励磁电流的输入，从而在气隙中形成稳定的磁场。

同步电机因其精确的控制能力和高效率，成为众多精密控制与高功率输出场合的首选。下一章节，我们将深入探讨同步电机的数学模型，并了解其详细的工作原理与转矩产生机制。

2. 同步电机数学模型

2.1 同步电机的工作原理

2.1.1 同步电机的电磁关系

同步电机的工作原理是基于电磁感应定律，通过电枢绕组中的交流电流与转子磁场之间的相互作用产生旋转电磁转矩。其电磁关系可以通过法拉第电磁感应定律和洛伦兹力定律来描述。交流电流在定子绕组中产生交变磁场，这个磁场与转子上的永磁体或励磁绕组产生的磁场相互作用，从而产生转矩驱动转子同步旋转。

• 法拉第电磁感应定律 ：表述了磁通量变化与感应电势之间的关系。具体来说，当磁通量通过导体回路变化时，在回路中会产生感应电动势。
• 洛伦兹力定律 ：说明了电流元素在磁场中所受的力的大小和方向，它解释了电流在磁场中的受力情况，这在同步电机中反映为电磁转矩的产生。

2.1.2 同步电机的转矩产生机制

同步电机的转矩产生机制涉及到电磁力与机械旋转的转化。在同步电机中，转矩是由于定子产生的旋转磁场与转子磁场相互作用的结果。转子的磁场可以由永久磁铁产生，也可以通过直流电激励产生的。

• 转子磁场的产生 ：永磁同步电机(PMSM)的转子由永久磁铁构成，而电磁同步电机则通过在转子绕组中通入直流电来产生磁场。
• 定子磁场的产生 ：定子由三相对称绕组构成，当三相对称电流通过绕组时，会在其中心产生旋转磁场。

当转子磁场与定子磁场相互作用时，它们之间的相对位置关系保持不变，产生一个恒定的电磁转矩，推动转子以同步速度旋转。电磁转矩的大小与定子和转子磁场的相对角度有关，其表达式可以表示为：

[ T_e = k \cdot \phi \cdot I_s \cdot \sin(\delta) ]

其中，(T_e) 代表电磁转矩，(k) 是比例常数，(\phi) 是转子磁链，(I_s) 是定子电流的幅值，(\delta) 是两磁场的相对角度。

2.2 同步电机的数学表达

2.2.1 电机电压方程的推导

电机电压方程是同步电机数学模型的重要组成部分，用于描述定子和转子绕组中电压与电流之间的关系。在同步电机的三相系统中，可以利用基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)来推导电压方程。

以三相绕组为例，电压方程可以表示为：

[ \left[\begin{array}{c} V_a \ V_b \ V_c \end{array}\right] = \left[\begin{array}{ccc} R_s & 0 & 0 \ 0 & R_s & 0 \ 0 & 0 & R_s \end{array}\right] \left[\begin{array}{c} I_a \ I_b \ I_c \end{array}\right] + \left[\begin{array}{ccc} L_s & M_{as} & M_{as} \ M_{bs} & L_s & M_{bs} \ M_{cs} & M_{cs} & L_s \end{array}\right] \frac{d}{dt} \left[\begin{array}{c} I_a \ I_b \ I_c \end{array}\right] ]

其中，(V_a, V_b, V_c) 是定子绕组的三相电压；(I_a, I_b, I_c) 是定子绕组的三相电流；(R_s) 是定子绕组的电阻；(L_s) 是定子绕组的自感；(M_{as}, M_{bs}, M_{cs}) 是定子绕组之间的互感。

2.2.2 电机磁链和电流的关系

磁链与电流之间的关系在电机的数学模型中是通过磁链方程来描述的。在同步电机中，磁链方程与电机绕组的结构以及转子的位置有关。对于简化的线性模型，磁链方程可以表示为：

[ \left[\begin{array}{c} \psi_a \ \psi_b \ \psi_c \end{array}\right] = \left[\begin{array}{ccc} L_a & M_{as} & M_{as} \ M_{bs} & L_b & M_{bs} \ M_{cs} & M_{cs} & L_c \end{array}\right] \left[\begin{array}{c} I_a \ I_b \ I_c \end{array}\right] ]

其中，(\psi_a, \psi_b, \psi_c) 分别为定子三相的磁链；(L_a, L_b, L_c) 为定子三相的自感。

2.2.3 电机转矩和功率的计算

在同步电机的数学模型中，转矩和功率的计算公式是评价电机性能的重要部分。转矩的计算公式已在2.1.2中给出，而电机的机械功率 (P_m) 和电气功率 (P_e) 的关系可以用以下公式来表达：

[ P_m = T_e \cdot \omega_s ]

这里，(\omega_s) 是同步角速度，单位是弧度每秒。电气功率 (P_e) 可以由定子的三相电压和电流计算得出：

[ P_e = V_a \cdot I_a + V_b \cdot I_b + V_c \cdot I_c ]

机械功率与电气功率的关系还考虑了电机的效率 (\eta)，因此有：

[ P_m = P_e \cdot \eta ]

通过调整定子电压和电流，可以控制同步电机的输出功率，从而满足不同的负载需求。

以上是对同步电机数学模型的基础章节内容的详细解析，下一章将深入探讨如何利用SIMULINK进行同步电机的建模。

3. SIMULINK同步电机建模

SIMULINK是MATLAB提供的一个用于模拟动态系统的图形化编程环境。它允许工程师创建包含控制系统、信号处理单元和通信系统的复杂模型，并进行仿真分析。同步电机模型的构建涉及到电机参数的准确设置和复杂交互关系的模拟。本章节将深入探讨如何在SIMULINK环境中搭建一个同步电机模型，并分析其建模过程中的关键步骤。

3.1 SIMULINK基础与建模环境介绍

3.1.1 SIMULINK的用户界面及功能

SIMULINK的用户界面由多个部分组成，允许用户以图形化的方式构建模型。主要组件包括模型浏览器（Model Explorer）、模型窗口（Model Window）、库浏览器（Library Browser）以及模型参数设置界面。用户可以通过拖拽不同的功能块（从库浏览器中选取）到模型窗口中来构建系统。

为了更高效地构建同步电机模型，SIMULINK提供了丰富的功能块，如信号源、数学运算单元、电机控制单元等。这些功能块可以模拟电机在不同工作状态下的动态行为。

3.1.2 建立同步电机模型的基本步骤

建立同步电机模型的基本步骤可以分为以下几个阶段：

1. 确定建模目标与需求：根据实际应用需求，明确模型需要达到的精确度和预期仿真功能。
2. 选择合适的同步电机模型类型：包括隐极式或凸极式模型，以及是否考虑饱和和磁滞效应。
3. 收集电机参数：需要从电机的技术手册中收集必要的参数，如电阻、电感、转动惯量等。
4. 在SIMULINK中搭建模型：根据电机的数学模型，在SIMULINK中搭建模型结构，连接各功能块。
5. 参数配置与验证：根据收集到的电机参数，配置模型中的参数，并进行仿真验证模型的准确性。
6. 运行仿真并分析结果：设定仿真参数，运行仿真，并使用Scope、To Workspace等模块收集并分析仿真结果。

3.1.3 代码块示例和逻辑分析

以下是一个SIMULINK模型中可能用到的代码块示例。请注意，在实际SIMULINK环境中，代码块是通过图形化的拖拽实现的，这里为了展示逻辑过程，使用伪代码表示：

% 伪代码，用于描述同步电机定子电压的计算过程
function [v_a, v_b, v_c] = stator_voltage_calculation(i_a, i_b, i_c, R, L, omega)
    % 参数说明：
    % i_a, i_b, i_c - 定子三相电流
    % R - 定子绕组电阻
    % L - 定子绕组电感
    % omega - 电机角速度

    % 计算定子电压
    v_a = R * i_a + L * diff(i_a) / dt + some_function_of_omega();
    v_b = R * i_b + L * diff(i_b) / dt + some_function_of_omega();
    v_c = R * i_c + L * diff(i_c) / dt + some_function_of_omega();
end

3.2 同步电机SIMULINK模型构建

3.2.1 定子模型的搭建

定子模型的搭建需要考虑电枢绕组的电阻、电感以及连接方式。在SIMULINK中，可以使用“Simscape Electrical”库中的“Three-Phase V-I Measurement”块来测量电流，并使用“Three-Phase Series RLC Branch”块来模拟电阻、电感和电容的组合。此外，需要定义电压源以模拟定子供电。

3.2.2 转子模型的搭建

转子模型主要关注电机的励磁方式。对于永磁同步电机，可以使用“Simscape Electrical”库中的“Permanent Magnet Synchronous Machine”块直接搭建转子模型，该块内含永磁体和转子的物理特性。对于电励磁同步电机，需要根据电机的实际励磁方式选用合适的励磁模块。

3.2.3 控制系统模型的集成

控制系统模型的集成是同步电机模型构建中非常重要的部分。控制系统通常包括电机控制器、转矩控制、速度控制等。可以使用“PID Controller”块或“State-Space”块来实现所需的控制策略。这些控制块与电机模型通过信号连接，确保控制系统能够准确地对电机进行控制。

3.2.4 代码块示例和逻辑分析

以下是一个简单的SIMULINK中控制系统模型的代码块示例：

% 伪代码，用于描述电机转速控制逻辑
function [u_ref, torque_command] = speed_control(speed, speed_ref)
    % 参数说明：
    % speed - 当前电机转速
    % speed_ref - 电机转速参考值
    % u_ref - 励磁电压参考值
    % torque_command - 转矩控制命令

    % 计算误差
    speed_error = speed_ref - speed;
    % PID 控制器
    [Kp, Ki, Kd] = get_pid_constants(speed_error);
    integral = integral + speed_error * dt;
    derivative = (speed_error - prev_error) / dt;
    u_ref = Kp * speed_error + Ki * integral + Kd * derivative;
    % 转矩命令计算
    torque_command = torque_function(u_ref);
end

通过本章节介绍的SIMULINK同步电机建模方法，可以构建出能够模拟同步电机动态行为的复杂模型。这一过程不仅需要对电机的工作原理有深入理解，同时需要熟悉SIMULINK工具的使用和电机控制策略的设计。

在下一章节中，我们将进一步探讨如何利用MATLAB中的S-函数，自定义控制策略以优化同步电机的仿真模型，从而实现更精确的仿真效果。

4. S-函数开发实现电机仿真

4.1 S-函数的概念与作用

4.1.1 S-函数定义及其重要性

S-函数（System Functions）是MATLAB中用于描述系统动态的一种特殊函数，是Simulink仿真软件的扩展接口。它允许用户用MATLAB、C、C++以及Fortran等编程语言编写自定义模块，以实现复杂的系统动态和控制逻辑。S-函数的名称来源于它们可以表达的“系统”(System)功能。

S-函数的重要性在于它为用户提供了灵活性，使得用户能够扩展Simulink的标准库。由于Simulink本身提供的模块数量有限，S-函数的引入，使得能够根据用户的需求，创建个性化的模型组件。这样，用户就可以把理论研究或工程实践中特有的算法或控制策略，封装成模块并集成到仿真模型中。

4.1.2 在MATLAB中编写S-函数的流程

在MATLAB中编写S-函数，大致可以分为以下几个步骤：

1. 创建一个新的S-函数模板。MATLAB提供了一些S-函数模板，可以根据需要选择适当的模板进行修改。
2. 定义S-函数的属性。这包括确定S-函数的输入输出端口数，以及每个端口的维度等。
3. 编写 Outputs 、 Update 、 Derivatives 等回调函数。这些函数分别对应模型输出计算、模型状态更新和状态导数计算。
4. 保存并测试S-函数。确保编写的S-函数能够正确集成到Simulink模型中，并且满足预定的功能需求。

接下来的子章节中，我们将展示一个简单的S-函数编写示例，以及相应的代码逻辑解释。

4.1.3 编写自定义S-函数代码示例

function msfcn_times_two(block)
% Level-2 MATLAB file S-Function for times two function.
%  The following S-function methods are supported by this S-Function:
%      Outputs - compute the outputs of the S-Function
%  To enable this S-Function to handle additional methods such as
%      Derivatives, Update, and InitializeConditions, define the methods
%      in the block's Level-2 MATLAB file, msfcn_times_two.m, and
%      choose 'MATLAB S-function' from the S-function Block's choice of block type in Simulink.

  setup(block);
function setup(block)
% Register number of input and output ports
block.NumInputPorts  = 1;
block.NumOutputPorts = 1;
% Setup port properties to be inherited or dynamic
block.SetPreCompInpPortInfoToDynamic;
block.SetPreCompOutPortInfoToDynamic;
% Override input port properties
block.InputPort(1).Dimensions        = 1;
block.InputPort(1).DirectFeedthrough = true;
% Override output port properties
block.OutputPort(1).Dimensions       = 1;
% Set block sample time to inherited
block.SampleTimes  = [-1 0];
% Set the block simStateCompliance to default (same as a built-in block)
block.SimStateCompliance = 'DefaultSimState';
% Register methods
block.RegBlockMethod('Outputs', @Output); 

% End of setup

function Output(block)
% Get input signal
u  = block.InputPort(1).Data;

% Get parameters from dialog box
k  = block.DialogPrm(1).Data;

% Compute output
y  = k * u;

% Set the output signal
block.OutputPort(1).Data = y;

在上述S函数中，我们定义了一个简单的乘以常数 k 的动态系统，它读取输入信号 u ，然后输出 k * u 。

4.2 S-函数在同步电机仿真中的应用

4.2.1 自定义S-函数的开发

在同步电机的仿真模型中，可能会需要自定义一些特殊的控制逻辑或动态行为，如自适应控制、非线性控制策略等。这些控制逻辑如果无法用标准的Simulink模块表达，就可以通过S-函数进行开发。

4.2.2 集成S-函数到SIMULINK模型

将自定义的S-函数集成到SIMULINK模型中非常简单。用户需要做的，仅仅是将S-函数模块拖拽到SIMULINK模型中，并且在S-函数模块的参数对话框中指定S-函数文件的路径。当模型开始运行时，MATLAB将加载S-函数并执行其中的回调函数，从而实现用户定义的动态行为。

4.2.3 S-函数的优化与调试

由于S-函数的执行效率可能直接影响到整个仿真的速度，因此在开发完成后，对S-函数进行优化是必要的。优化措施包括减少不必要的计算、避免在回调函数中使用全局变量、使用内联函数和预分配数组等。调试S-函数时，可以利用MATLAB的调试器逐步执行回调函数，观察变量的变化，同时查看Simulink模型的运行状况。

4.3 同步电机仿真中S-函数的具体应用案例

为了更好地理解如何在同步电机仿真中应用S-函数，我们下面将通过一个简单的案例，说明如何通过S-函数实现一个简单的控制逻辑。

假设我们希望在同步电机的仿真模型中加入一个简单的P控制器，来调整电机的转速。P控制器需要的参数包括比例系数（Kp），而它的输入是转速的误差（即参考转速与实际转速的差值），输出是调整的电压值。

function msfcn_pcontroller(block)
% Level-2 MATLAB file S-Function for P controller.
%  The following S-function methods are supported by this S-Function:
%      Outputs - compute the outputs of the S-Function
%  To enable this S-Function to handle additional methods such as
%      Derivatives, Update, and InitializeConditions, define the methods
%      in the block's Level-2 MATLAB file, msfcn_pcontroller.m, and
%      choose 'MATLAB S-function' from the S-function Block's choice of block type in Simulink.

  setup(block);

function setup(block)
% Register number of input and output ports
block.NumInputPorts  = 1;
block.NumOutputPorts = 1;
% Setup port properties to be inherited or dynamic
block.SetPreCompInpPortInfoToDynamic;
block.SetPreCompOutPortInfoToDynamic;
% Override input port properties
block.InputPort(1).Dimensions        = 1;
block.InputPort(1).DirectFeedthrough = true;
% Override output port properties
block.OutputPort(1).Dimensions       = 1;

% Set block parameters
block.DialogPrm(1).Name       = 'Kp';
block.DialogPrm(1).Type       = 'double';
block.DialogPrm(1).Value      = 1;
block.DialogPrm(1).Promote   = true;
block.DialogPrm(1).Position   = [100 50 120 14];
block.DialogPrm(1).StringMode = 'text';
block.DialogPrm(1).String     = '1';

% Set block sample time to inherited
block.SampleTimes  = [-1 0];
% Register methods
block.RegBlockMethod('Outputs', @Output); 

% End of setup

function Output(block)
% Get input signal
error = block.InputPort(1).Data;

% Get parameters from dialog box
Kp    = block.DialogPrm(1).Data;

% Compute output
u     = Kp * error;

% Set the output signal
block.OutputPort(1).Data = u;

在上述代码中，S函数实现了一个比例控制器，其比例系数 Kp 作为参数可以调整。需要注意的是，在实际的仿真中，必须将参考转速输入到这个P控制器，并将控制器的输出连接到同步电机模型的相应输入端，以完成整个控制回路的构建。

4.4 S-函数优化与调试的具体操作

在仿真运行后，如果性能不符合预期，或者仿真过程中出现了不正确的行为，就需要对S-函数进行调试。为了调试S-函数，我们通常会开启MATLAB的调试器，对S-函数中定义的回调函数进行逐步执行，检查变量的值以及它们的变化是否合理。

MATLAB的调试器支持单步执行（Step）、步入（Step Into）、步出（Step Out）等多种调试方式。使用这些调试方式，我们可以从不同的层级检查代码的执行细节，从而快速定位问题所在。调试过程中，MATLAB会高亮当前执行的代码行，我们可以观察运行时变量的值，或直接修改这些值来测试不同的运行情况。

除了MATLAB的调试器，Simulink模型的调试也可以通过Simulink的诊断功能来辅助完成。在仿真设置中，可以开启“诊断”选项，根据需要设置错误检测的敏感级别，通过模型的运行结果来获得可能存在的问题提示。

4.5 S-函数使用常见问题与解决策略

在使用S-函数进行同步电机仿真的过程中，可能会遇到一些常见的问题，如S-函数加载失败、回调函数执行错误、仿真运行速度慢等。针对这些问题，我们可以采取以下策略：

• S-函数加载失败 ：检查S-函数文件的路径是否正确，确保文件名和指定的名称一致；检查文件中是否有语法错误，或者回调函数是否缺少必要的定义。
• 回调函数执行错误 ：利用MATLAB的调试器，逐步执行回调函数代码，查看错误信息，根据错误提示找到问题所在。常见问题包括输入输出端口的定义与模型不匹配、执行回调函数时缺少必要的参数等。
• 仿真运行速度慢 ：检查S-函数代码，简化计算过程，尽可能减少在回调函数中的循环和条件判断；利用MATLAB的性能分析工具（如 profile ）来分析代码执行时间，找出性能瓶颈。

在实际开发和使用S-函数的过程中，通常需要结合具体的仿真需求和遇到的问题进行详细的分析和调试。通过不断优化S-函数代码，并结合Simulink模型调试工具，可以有效地解决使用S-函数进行同步电机仿真的问题。

5. 同步电机控制策略与仿真优化

5.1 同步电机的控制方法

同步电机的控制策略在保证电机高效、稳定运行中扮演着重要角色。根据不同的应用场景，可以采用多种控制方法。

5.1.1 常用的同步电机控制策略

• 矢量控制（Field-Oriented Control, FOC） ：通过坐标变换，将同步电机的电流矢量分解为与转子磁场同步旋转的转矩分量和励磁分量，实现对电机的精确控制。
• 直接转矩控制（Direct Torque Control, DTC） ：通过控制电机的转矩和磁链的大小和方向，直接对电机的输出进行控制，避免了复杂的坐标变换。
• 恒压频比控制（V/F Control） ：适用于对动态性能要求不高的场合，通过保持电压与频率的恒定比例来控制电机。

5.1.2 控制策略的选择依据

选择合适的同步电机控制策略需要考虑以下因素：

• 应用需求 ：例如，需要高动态性能时，矢量控制和直接转矩控制更为适合。
• 成本预算 ：矢量控制和直接转矩控制通常需要高性能的处理器和传感器，成本相对较高。
• 电机类型 ：不同类型的电机可能更适合某一种控制策略，如永磁同步电机适合使用矢量控制。

5.2 同步电机仿真参数设置

正确的参数设置是进行仿真测试前的重要步骤，可以确保仿真的准确性和可靠性。

5.2.1 参数设置的基本原则

• 真实性 ：参数应尽可能接近实际电机的物理参数。
• 全面性 ：考虑所有可能影响电机性能的因素，如温度、负载等。
• 可调性 ：参数应设计为可调整的，以便于进行优化和故障模拟。

5.2.2 特殊工况下的参数调整

针对不同工况，如高负载、高/低温环境，需要对参数进行调整：

• 高负载 ：增加电机的电流限值，调整电压补偿系数。
• 高温环境 ：可能会降低电机效率和磁通量，需要调整相应的控制参数。

5.3 同步电机仿真结果的分析与验证

分析仿真结果是检验控制策略和参数设置是否合理的最后一步。

5.3.1 结果分析的方法

• 波形分析 ：观察电压、电流、转速和转矩等波形是否平稳，是否存在过冲或振荡。
• 性能指标评估 ：如效率、功率因数和稳定运行范围等。
• 故障模拟 ：在仿真环境中加入故障，评估控制策略的鲁棒性。

5.3.2 仿真实验的有效性验证

• 与实际数据对比 ：将仿真结果与实验数据或以往的工程案例数据进行对比。
• 灵敏度分析 ：分析关键参数变化对系统性能的影响，检验系统的鲁棒性。
• 多次运行验证 ：进行多次仿真实验，确保结果的重复性和一致性。

示例代码段

在MATLAB/Simulink中进行同步电机仿真时，可能会用到如下代码段来设置仿真参数：

% 设置仿真时间
simTime = 10; % 仿真10秒

% 设置电机参数
motorParameters = struct('Ra', 0.5, 'Ls', 0.02, 'Lm', 0.06, 'Rs', 0.5);

% 仿真模型的参数设置
sim('synchronousMotorModel', simTime);

这段代码仅是一个简单的示例，实际的仿真模型会更加复杂，需要根据具体情况进行调整。

通过以上章节的介绍，我们详细探讨了同步电机的控制策略、仿真参数的设置，以及如何分析和验证仿真的结果。这些步骤和技巧对于设计高效的同步电机控制系统至关重要，能够帮助工程师在仿真环境中准确评估和优化电机性能。

本文还有配套的精品资源，点击获取

简介：同步电机在电力系统和工业领域有着广泛的应用。本文介绍了使用MATLAB及其SIMULINK环境进行同步电机建模和仿真的关键步骤和概念，包括电机的基本结构、数学模型、控制策略、仿真参数设置、结果分析、优化设计及验证。通过这些实践指南，读者可以深入理解同步电机的工作原理和性能，并优化电机设计。提供资料包含MATLAB代码、SIMULINK模型和文档，以辅助学习和研究。

本文还有配套的精品资源，点击获取