的不定积分_不定积分解题策略

不定积分是高等数学和数学分析的重要内容，是整个积分学的基础。作为求导函数的逆运算，不定积分比求导函数数要难得多。本期讲一讲不定积分解题策略的选择，下期就不定积分求解的一些技巧做一个全面梳理，敬请关注。虽然求不定积分需要有足够的经验，但也要讲究一定的解题策略，解题策略可以概括成一句话：

 一凑二换三分部 变形分插配选殊

1. 凑微分

凑微分是不定积分最根本的方法。主要体现在两方面，一是凡积必凑，不管用其他什么积分方法，最后一步必然要凑微分；二是凡凑必快，凑微分能解决问题时，一定比用其他积分方法更快捷。因此，面对不定积分题目，我们首先要尝试凑微分法解决。

理论上说，所有题目，只要有显式原函数，就一定能使用凑微分解决，这只要将原函数求导的过程倒过来写就是凑微分进行积分的过程。例如

例1. 求不定积分

解 大多数同学看到此题首先会使用变量代换u=x^1/2。事实上凑微分更方便，根据求导过程

此过程倒着写就是凑微分过程

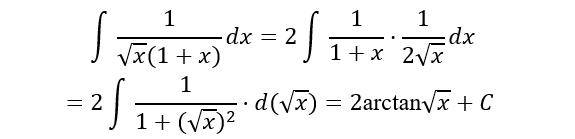
是对大多数不定积分题目，我们并不知道原函数，特别是一些相对“生疏”的被积函数，我们要凑微分还是比较困难的。这就需要我们有敏锐的观察，有丰富的经验。这些经验来源于对大量函数求导过程的细节再现。再如：

例2. 求不定积分

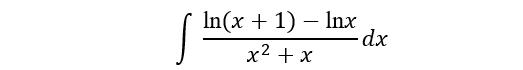
解

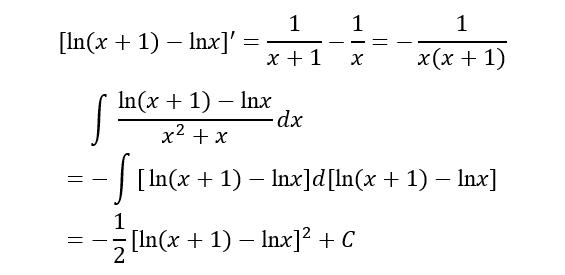
这样的微分方法，简便快捷。解答者能观察到，在被积函数中，分子的导数是分母的负倒数。从而很容易地将被积函数分解，使得

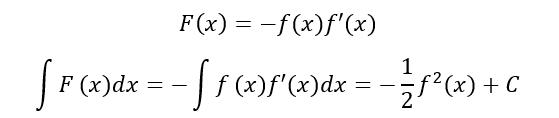
要具备足的洞察力，就需要有大圣的火眼金睛，这需要在太上老君的丹炉里垂炼。

所以说勤题，善总结才是王道。类似的题目很多，再如

例3. 求不定积分

解

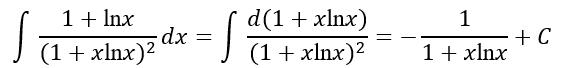
不是每不定分的被积函数F(x)都可分解成乘积f(x)f'(x)的形式，更一般的情况是将被积函数分解成乘积g(f(x))f'(x)，这样就有

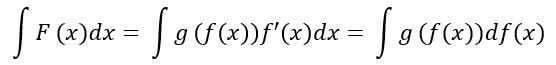
这时我们令f(x)=u，这就是变量代换。

可以看出，凑微分的关键在于如上式对被积函数的因子分解，分解是否有效取决于是否有利于函数g(u)的积分。

2.变量代换

可以看出，变量代换后不定积分变为

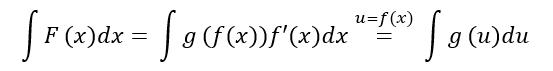
这时我们可以对新的积函数g(u)重复上述步骤。

如果对g(u)积分有可行的处理方法，说明前面的变量代换是成功的，否则前面的变量代换并不是可取的。变量代换的目的也是为了更好地凑微分，这句话意思是，对于经过变量代换后的被积函数，更容易变形为易凑微分的形式。代换就像技术性整容，为了塑造完美的形象而变成另一个自己。

如前面的例2

例4.(续例2)求不定积分

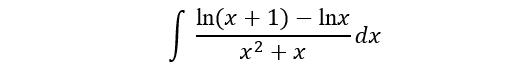
解法二 作变量代换

可以看出，经过变量代换，积函数有了极大的简化。

例5. (续例3)求不定积分

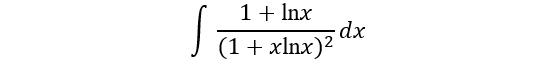
解法二 试试用变量代换法按照例3解法，可以设t=1+xlnx，显然从中解不出x来，也就无法计算dx。如果有凑微分经验，可知

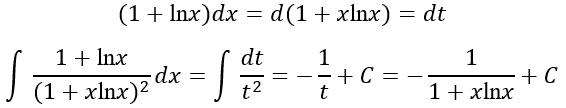
当然也可以作这样的变换

接来的步骤依然需要凑微分。见无论如何凑微分是必须的。

还有一类型题目，被积函数经过求导才有利于凑微分，这时就必须用分部积分法。

3.分部积分

当被积函数中含有一些因子，将这些因子求导后就可简化函数，或者求导后与其他部分运算可形成易凑微分的形式，这时可考虑分部积分法。本质上看分部积分是将被积函数分成两部分，一部分进行求导运算，另一部分进行积分运算，从形式上看是u(x)dv(x)→v(x)du(x)，两个函数位置的交换，交换后会有不同的效果。

例6. 求不定积分

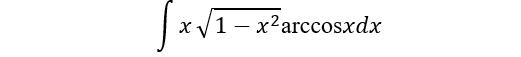
解 arccos x求导即可简化积函数。进行分部积分

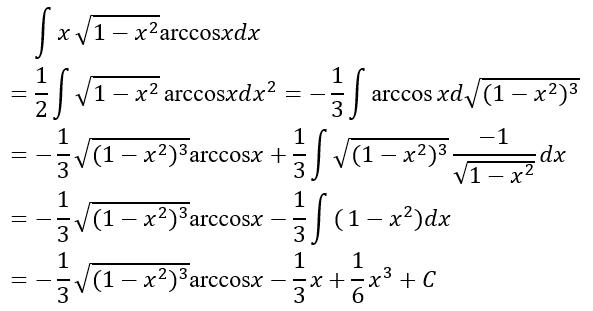
有时被积函数即使经过变量代换或者分部分，也不能像上面所述可以直接分解为乘积g(f(x))f'(x)的形式，需要经过变形后才能做这样的分解。

4.恒等变形

事实上，变量代换和分部积分也是恒等变形，不过是被积函数和微分符号一起参与变形而已。本小节中的恒等变形仅指被积函数的变形。

被积函数的恒等变形千变万化，分解、插、配因子，等等。还可以选择一些特殊的数学运算，如有理化、裂项、积化和差、和差化积，等等不胜枚举，总之数学中平时使用的恒等变形在不定积分中都可能用到。大多数不定积分，被积函数都需要经过恒等变形才能凑微分或变量代换或有效的分部积分。下面仅举一例

例7. 求不定积分

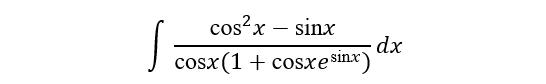
解 由于

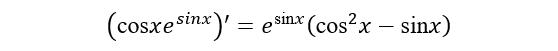
则可在原积分被积函数中，分分母同乘以因子^{sin x}，这样就可以将分子凑微分了

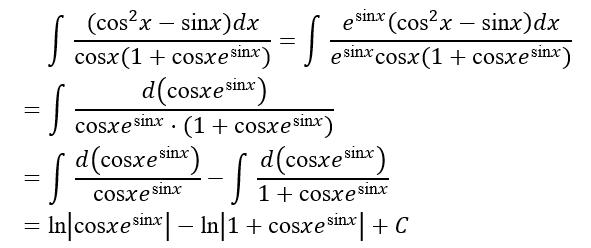
5.小结

不定积分的解法变化多，过程复杂，要多做练习，善于总结规律，正是：

 一凑二换三分部， 变形分插配选殊； 苦练善思是王道， 根本大法凑微分。