Chapter 5
Gradient Temporal-Difference Learning with Linear Function Approximation
本章提供了线性函数近似情况下梯度-TD算法的核心思想和理论结果。在这里,我们在Baird(1995;1999)的工作基础上,探讨了用于线性函数逼近的时差学习的真正随机梯度下降算法的发展。
特别是,我们引入了三种新的TD算法,与线性函数逼近和off-policy训练兼容,其复杂度仅以函数逼近器的大小为线性扩展。第一种算法,GTD,估计TD(0)算法的the expected update
vector,并对其L2范数进行随机梯度下降;即norm of the expected TD update,也称为NEU(见第三章)。
在第5.3节中,我们证明了在通常的随机逼近条件和off-policy数据的i.i.d.假设下,GTD是稳定的,并且收敛于TD-解。第二和第三种算法,GTD2和TDC(带有梯度修正项的TD),和GTD一样被推导并证明是收敛的,但使用了预测的贝尔曼误差目标函数(见第三章),收敛速度明显加快(但仍然没有传统TD快)。
在我们对小型测试问题的实验中,这些算法的学习率与TD(0)进行了比较。为了进一步了解这些新算法在大规模问题上的表现,David Silver在一个具有一百万个特征的计算机围棋应用程序中实现了梯度TD算法(见Sutton, Maei, et al. 2009)。
我们的实证结果表明,TDC的收敛速度快于GTD2和GTD,但在on-policy问题上,它仍然可能比TD(0)慢。所有这些新的线性算法都将线性TD(0)扩展到有收敛保证的off-policy学习中,而计算要求却增加了一倍。
实验结果表明,TDC算法是GTD和GTD2算法中效率最高的算法。因此,在接下来的章节中,我们将构建基于TDC的新算法
5.1 Derivation of the GTD algorithm
接下来,我们将介绍导致GTD算法的想法和梯度下降的推导。正如前一章所讨论的(见第4.1节中的off-policy i.i.d.表述),我们考虑i.i.d.样本 ( S k , R k , S k ′ ) k ≥ 0 (S_k,R_k, S'_k)_{k≥0} (Sk,Rk,Sk′)k≥0,由过渡的起始状态、过渡的奖励以及过渡的结束状态组成。对于线性函数逼近的情况,第k个对应于三元组 ( ϕ k , R k , ϕ k ′ ) (\phi_k,R_k, \phi'_k) (ϕk,Rk,ϕk′),其中 ϕ k = ϕ ( S k ) , ϕ k ′ = ϕ ( S k ′ ) \phi_k=\phi(S_k),\phi'_k=\phi(S'_k) ϕk=ϕ(Sk),ϕk′=ϕ(Sk′)。
注意,起始态分布为μ,状态转移概率为P,向量 E [ δ ϕ ] \mathbb E[\delta\phi] E[δϕ]是expected TD update,可被视为当前解θ中的误差。向量应该是零,所以它的范数是我们离TD解有多远的度量。我们对时间差分学习的梯度下降分析的一个显著特征是,我们使用该向量的L2范数作为我们的目标函数:
当 E [ δ ϕ ] = 0 \mathbb E[δ\phi]=0 E[δϕ]=0时,它的最小值为0。 这个目标函数的梯度方向为
如果梯度可以写成一个单一的期望值,这是直接的,但是这里我们有两个期望值的乘积。我们不能同时对它们进行抽样,因为抽样乘积会因为它们的相关性而产生偏差。然而,我们可以存储其中一个期望值的长期、准稳定的估计值,然后对另一个期望值进行采样。问题是,哪个期望值应该被估计和存储,哪个应该被采样?这两种方法似乎都会导致我们采用不同的算法。
首先,让我们考虑通过forming and storing第一个期望值的单独估计得到的算法;也就是矩阵 A = E [ ϕ ( ϕ − γ ϕ ′ ) T ] A=\mathbb E[\phi(\phi-γ\phi')^T] A=E[ϕ(ϕ−γϕ′)T]。这个矩阵可以根据经验直接估计为所有先前观察到的样本外积 ϕ ( ϕ − γ ϕ ′ ) T \phi(\phi-γ\phi')^T ϕ(ϕ−γϕ′)T的简单算术平均值。请注意,在任何固定策略的策略评价问题中,A是一个固定的统计量;它不依赖于θ,如果θ发生变化,也不需要重新估计。让 A k A_k Ak是观察了前k+1个样本后对A的估计, ( ϕ 0 , R 0 , ϕ 0 ′ ) , . . . , ( ϕ k , R k , ϕ k ′ ) (\phi_0,R_0, \phi'_0),..., (\phi_k,R_k, \phi'_k) (ϕ0,R0,ϕ0′),...,(ϕk,Rk,ϕk′) 。那么这个算法的定义是
其中 θ 0 θ_0 θ0是任意的, δ k = R k + γ θ k T ϕ k ′ − θ k ϕ k , ( α k ) k ≥ 0 δ_k = R_k + γθ^T_k\phi'_k - θ_k\phi_k,(αk)_{k≥0} δk=Rk+γθkTϕk′−θkϕk,(αk)k≥0是一系列的步长参数,可能随着时间的推移而减少。我们在此不进一步考虑上述算法,因为它需要O(d2)内存和每个时间步长的计算。
估计梯度(5.1)的随机逼近算法的第二种方法是形成并存储第二个期望的估计值,即向量 E [ δ ϕ ] \mathbb E[δ\phi] E[δϕ],并对第一个期望进行采样,即 E [ ϕ ( ϕ − γ ϕ ′ ) T ] \mathbb E[\phi(\phi-γ\phi')^T] E[ϕ(ϕ−γϕ′)T]。让 u k u_k uk表示观察前k个样本后对 E [ δ ϕ ] \mathbb E[δ\phi] E[δϕ]的估计, u 0 = 0 u_0=0 u0=0。 GTD算法定义为
其中 θ 0 θ_0 θ0是任意的, δ k δ_k δk是使用 θ k θ_k θk的TD误差, ( α k , β k ) k ≥ 0 (α_k, β_k)_{k≥0} (αk,βk)k≥0是正的步长参数序列,可能随时间的推移而减少。请注意,如果乘积是从右到左形成的(formed right-to-left),那么整个计算的时间步长为O(d)。
然而,与TD(0)相比,GTD是一个缓慢的算法。In other words it is poorly conditioned。让我们考虑这种情况:假设我们可以准确地计算 u u u,也就是说。
其中A和b的定义见方程(2.13)。因此,通过将u(θ)的精确值插入θ的更新中,在期望值中,GTD的更新是由矩阵 A T A A^TA ATA驱动。为了更好地看到这一点,请注意,从方程(5.1)中我们得到。
从数值分析的概念来看, A T A A^TA ATA的条件数总是比A差-注意-A是预期TD(0)更新的基础矩阵。因此,在TD(0)收敛的问题上,GTD的渐进收敛率通常比TD(0)差很多。
From concepts of numerical analysis, the condition number of A T A A^TA ATA is always worse than A—notice −A is the underlying matrix for the expected TD(0) update. As such, GTD’s asymptotic rate of convergence is usually much worse than TD(0) on problems where TD(0) converges.
在下一节中,我们开发了两种新的算法,GTD2和TDC,基于均方投影贝尔曼误差目标函数,根据经验,这两种算法比GTD算法更快。
5.2 Derivation of the GTD2 and TDC algorithms
在这一节中,我们推导出两种新的算法,它们使用均方投影贝尔曼误差作为其目标函数(见公式3.3)。我们首先在向量-矩阵量和相关的统计期望项之间建立一些关系。
利用这些关系,预期的目标可以写成如下的形式
就像在上一节中,我们使用第二个可修改的参数 u ∈ R d u∈\mathbb R^d u∈Rd来形成NEU目标函数梯度中除一个期望外的所有准稳定估计(从而避免了对两个独立样本的需要),在这里,我们将使用一个可修改的参数 w ∈ R d w∈\mathbb R^d w∈Rd,这也涉及到计算逆矩阵。具体来说,我们使用一个传统的线性预测器,使w估计为
Just like in the previous section, which we used a second modifiable parameter u ∈ R d u∈\mathbb R^d u∈Rd to form a quasi-stationary estimate of all but one of the expectations in the gradient of the NEU objective function (thereby avoiding the need for two independent samples), here, we will use a modifiable parameter w ∈ R d w∈\mathbb R^d w∈Rd, which also involves computing the inverse matrix.Specifically, we use a conventional linear predictor which causes w to estimate
这看起来与我们在监督学习中通过用监督信号替换δ而得到的解决方案相同(注意 w ( θ ) = E [ ϕ ϕ T ] − 1 u ( θ ) ) w(θ)=\mathbb E[\phi\phi^T]^{-1}u(θ)) w(θ)=E[ϕϕT]−1u(θ))。利用这一点,我们可以将MSPBE目标函数的负梯度写为
我们称之为GTD2算法。注意,(5.8b)更新中没有逆矩阵。我们可以看到,通过将 θ k θ_k θk固定为θ,w更新导致LMS解,即 w ( θ ) = E [ ϕ ϕ T ] − 1 E [ δ ( θ ) ϕ ] w(θ)=\mathbb E[\phi\phi^T]^{-1}\mathbb E[δ(θ)\phi] w(θ)=E[ϕϕT]−1E[δ(θ)ϕ]。
我们的主要算法TDC的推导从梯度的相同表达式开始,然后采用稍微不同的路径。也就是说,
然后采样,得到以下O(d)算法,我们称之为带梯度修正项的线性TD,简称线性TDC:
其中 w k w_k wk由(5.8b)产生,如同GTD2。注意θk的更新是两个项的总和,第一个项与传统线性TD的更新(2.10)完全相同。第二项基本上是对TD更新的调整或修正,使其遵循MSPBE目标函数的梯度。如果第二个参数向量初始化为 w 0 = 0 w_0=0 w0=0,并且βk很小,那么这个算法一开始就会做出与传统线性TD几乎一样的更新。
TDC算法(5.10),是在一个给定的子样本袋上推导出来的,其形式是与行为和目标策略样本转换相匹配的三元组 ( S k , R k , S k ′ ) (S_k,R_k, S'_k) (Sk,Rk,Sk′)。如果我们想使用所有的数据呢?注意,数据是根据行为策略 π b π_b πb产生的,而我们的目标是学习目标策略π。
Derivation of Linear TDC for importance-sampling scenario: 我们想最小化的目标函数是 J ( θ ) = ∣ ∣ V θ − Π T π V θ ∣ ∣ μ 2 J(θ)= ||V_θ-ΠT^πV_θ ||^2_μ J(θ)=∣∣Vθ−ΠTπVθ∣∣μ2,然而,由于数据是根据行为策略 π b π_b πb产生的,我们使用重要性抽样。使用定理1(在第四章),和公式(4.2),我们得到。
根据线性TDC推导,得到以下算法(基于重要性加权场景的线性TDC算法):








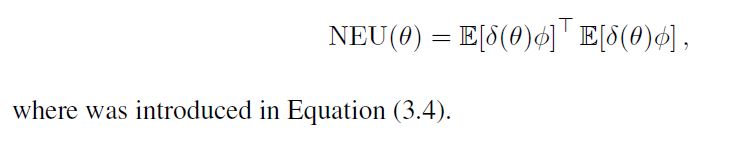
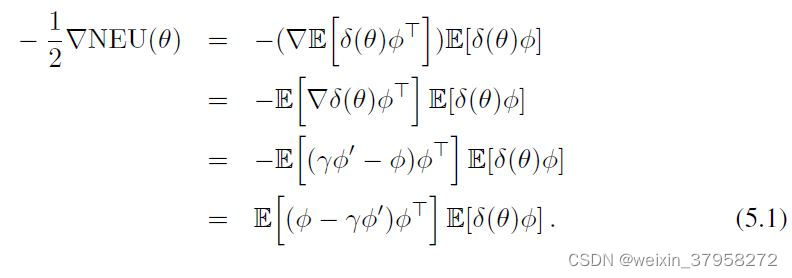
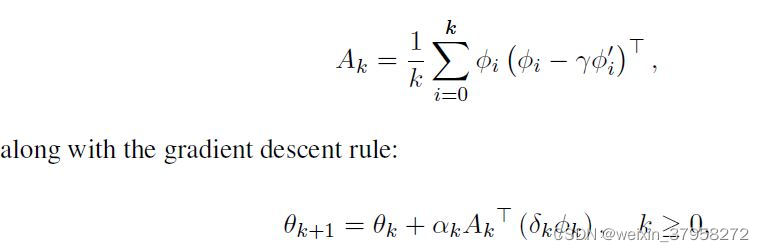
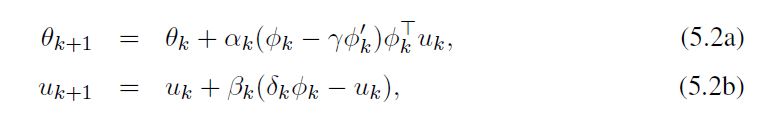
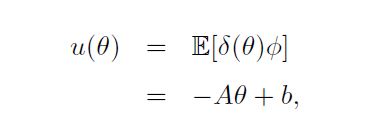
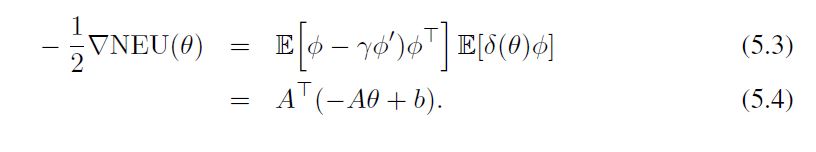
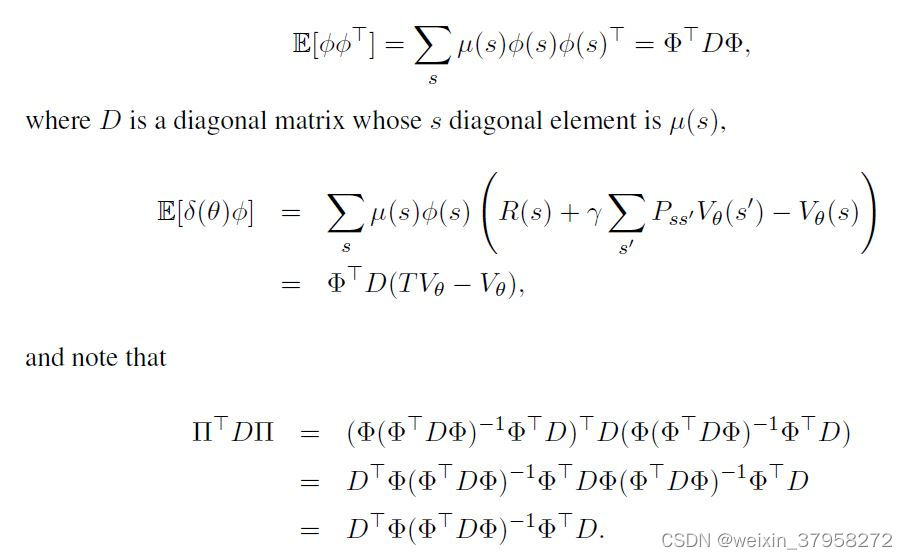
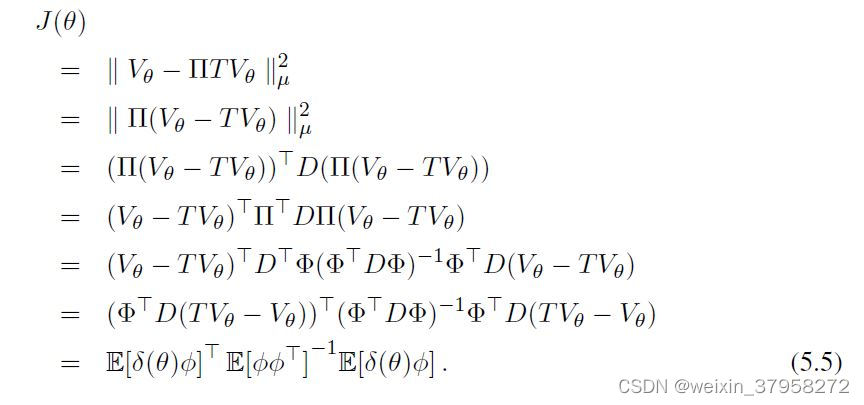
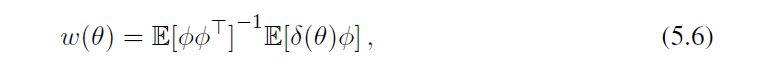


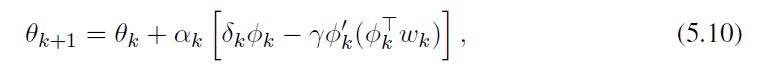
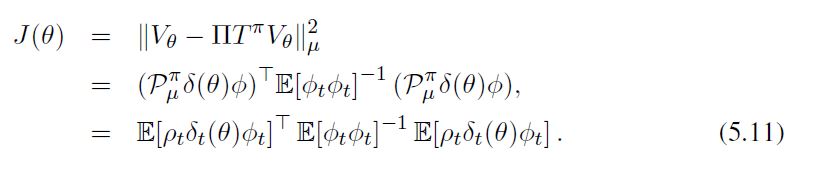
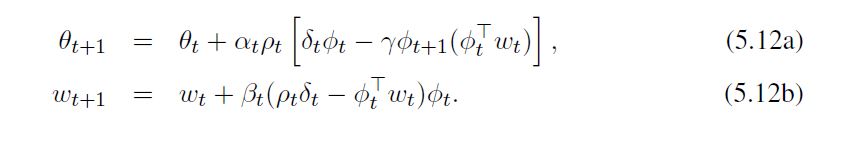














 4086
4086











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








