香港城市大学低空经济下UAV导航通信！O-VIB：面向任务的空地协同视觉导航通信框架-CSDN博客

本文链接：https://blog.csdn.net/weixin_37990186/article/details/148336473

作者：Zhengru Fang*, Zhenghao Liu‡, Jingjing Wang‡, Senkang Hu*, Yu Guo*, Yiqin Deng*, Yuguang Fang*
单位：
- * 香港赛马会STEM智慧城市实验室 & 香港城市大学计算机科学系
- ‡ 北京航空航天大学网络与空间安全学院
论文题目：Task-Oriented Communications for Visual Navigation with Edge-Aerial Collaboration in Low Altitude Economy
论文链接：https://arxiv.org/abs/2504.18317v3
代码链接：https://github.com/fangzr/TOC-Edge-Aerial

背景介绍

低空经济（Low Altitude Economy, LAE）时代，轻型无人机（UAV）被广泛应用于物流、巡检与应急响应等场景。然而，城市中 GPS 信号失效（如高楼遮挡、干扰）严重制约其定位性能。视觉导航成为主流替代方案，但受限于轻型无人机的算力和通信能力，目前大部分基于深度学习、大语言模型的视觉导航算法难以部署在资源严重受限的无人机平台。本研究借助边缘节点的计算卸载服务与面向任务的通信（Task-Oriented Communications, TOC）方法，提出一种基于空地协同的无人机视觉定位新框架，实现无GPS定位、极低通信开销的情况下的高效无人机视觉定位。

主要贡献

创新编码器 O-VIB：设计了融合正交性约束与自动相关性判定（ARD）的压缩编码器，压缩特征同时保障定位精度。
多视角UAV数据集：机载摄像头“前、后、左、右、俯视”五个视角数据，包含 357,690 帧对齐的 RGB、深度与语义图像，模拟城市中无人机采集的多视角摄像头数据。
实地部署与验证：在 Jetson Orin NX 与 Raspberry Pi 构建的测试平台上部署系统，验证其在带宽受限下的定位精度与延迟表现。

问题定义

目标是：在通信受限（带宽上限为 $C_{\max}$ ）条件下，最小化无人机定位误差：

$\min_{\Theta} \mathbb{E} \left[\| \hat{Y}_t - Y_t \|^2 \right], \quad \text{s.t.} \quad C(Z_t) \leq C_{\max}$

其中：

$X_t$ ：多视角提取的高维特征；
$Z_t$ ：压缩后的潜在表示；
$\hat{Y}_t$ ：推理后的定位；
$C(Z_t)$ ：通信开销函数。

系统框架总览

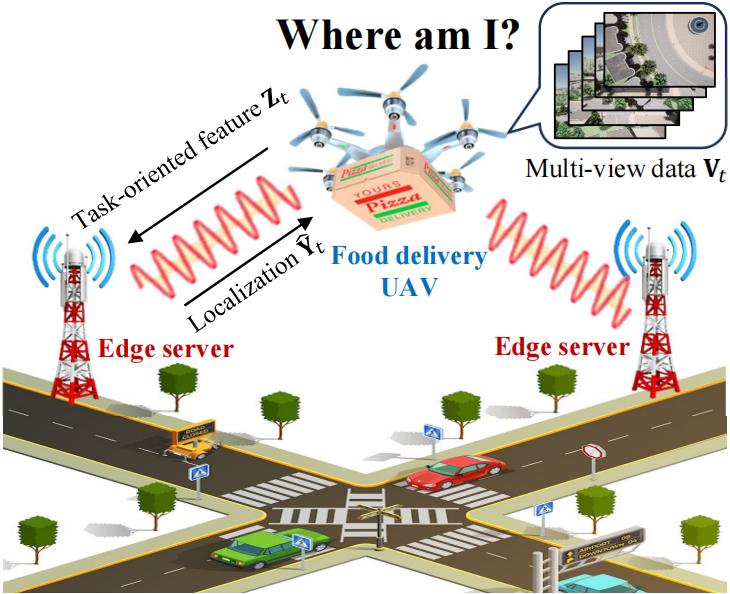
System Architecture

多摄像头UAV + 无线通信 + 边缘服务器

核心思路：多视角图像提取 → 特征压缩 → 传输至边缘 → 推理定位

前端UAV采集5路视角（前、后、左、右、下）
后端边缘服务器进行数据库匹配与融合定位
有效权衡定位精度与带宽使用

算法框架设计

多视角感知 + CLIP特征提取

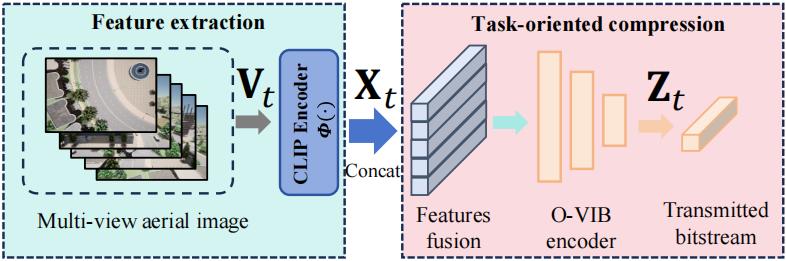
Encoder Architecture

搭载 5 视角摄像头（前后左右下），通过 CLIP-ViT 编码器提取每帧 512 维嵌入，拼接形成全局视觉描述符。

信息瓶颈（Information Bottleneck）理论用于数据压缩

经典信息瓶颈理论Information Bottleneck（IB） 要求在压缩 $X$ 的同时保留对任务标签 $Y$ 预测的最大信息量，形式化为

$\min_{q_\phi(z|x)}\; I(Z;X)-\beta\,I(Z;Y), \tag{1}$

其中 $I(\cdot;\cdot)$ 为互信息， $\beta$ 控制“保留 vs. 压缩”。在本场景中，瓶颈变量 $Z_t$ 直接通过无线链路发送，因此我们把 链路容量 纳入约束（或写成拉格朗日乘子）得到

$\min_{\Theta}\; \mathbb{E}\!\bigl[\lVert\hat Y_t-Y_t\rVert^2\bigr] \;+\;\lambda\,I(Z_t;X_t), \quad\text{s.t.}\;C(Z_t)\le C_{\max}, \tag{2}$

并用 K-L 上界 将 $I (Z; X)$ 近似为

$I(Z;X)\;\le\; \mathbb{E}_{p(x)} \bigl[ D_{\mathrm{KL}}\!\bigl(q_\phi(z|x)\,\|\,p(z)\bigr) \bigr]. \tag{3}$

若把 $p(z)=\mathcal N(0,I)$ 、 $q_\phi(z|x)=\mathcal N(\mu_\phi(x),\sigma_\phi^2(x)I)$ ，则 (3) 可写成元素级的“重参数化 + KL”项，方便反向传播。

O-VIB （Orthogonally-constrained VIB）编码器

核心思想：引入信息瓶颈（IB）理论，在保持定位信息的同时压缩无关冗余。
关键机制：
- Automatic Relevance Determination（ARD）：自动淘汰不重要的潜变量维度（使用Log-Uniform先验）；
- 正交性约束：避免不同维度冗余重合，确保信息有效分布。

符号	含义	与传统 VIB 的差别
O-VIB	Orthogonally-constrained VIB	在常规 VIB 的 KL 瓶颈外，加入正交正则 $\lVert WW^\top-I\rVert_F^2$ ，确保各潜维度互补、避免冗余；同时引入 ARD 取代固定先验。
$W\in\mathbb R^{d\times m}$	编码投影矩阵	Vanilla VIB 只需输出 $(\mu,\sigma)$ ；O-VIB 进一步要求 $W$ 的行正交。
$D_{\text{ARD}}(x)$	自动相关性判别惩罚	用可学习方差 $\sigma_k^2(x)$ 近似 KL，与正交项一同塑形潜空间。

在带宽受限 ( $C_{\max}$ ) 场景，可把 $\beta$ 视作对链路费用的“物价系数”。

ARD 机制的数学推导

潜变量假设
$z_k=\mu_k+\sigma_k\epsilon,\quad \epsilon\sim\mathcal N(0,1).$
对数均匀先验
给每一维方差设置 $p(\log\sigma_k^2)=\text{const}$ ，等价于
$p(z_k)=\int\! \mathcal N\!\bigl(0,\sigma_k^2\bigr)\;p(\log\sigma_k^2)\,d\log\sigma_k^2 \;\propto\;\frac{1}{|z_k|},$
产生“重尾”分布：小权重易被压向零，大权重得到保留。
KL 项近似
$D_{\text{ARD}}(x)\approx -\tfrac12\sum_{k=1}^{d}\log\sigma_k^2 +\tfrac12\sum_{k=1}^{d}\!\frac{\mu_k^2}{\sigma_k^2} +\text{const}, \tag{4}$
其中第一项鼓励 $\sigma_k^2\!\to\!\infty$ （弃用通道），第二项鼓励 $\mu_k\!\to\!0$ 。
训练后若 $\sigma_k^2$ 较大且 $\mu_k\!\approx\!0$ ，该通道可 硬剪枝，实现自适应降维。
与 VIB 的区别
- Vanilla VIB：KL 与固定 $p(z)=\mathcal N(0,I)$ ；所有维度同等“纳税”。
- O-VIB：KL 被 ARD 重写为 (5)，使 无用维的惩罚更高，配合正交项迫使剩余维度互补，从而在同带宽下获得更高定位精度、更低冗余熵。

最终训练的损失函数设计如下

$\boxed{ \mathcal L= \underbrace{\lVert x-\hat x\rVert^2}_{\text{重建}} +\alpha\,\underbrace{\lVert y-\hat y\rVert^2}_{\text{定位}} +\beta\,\underbrace{D_{\text{ARD}}(x)}_{\text{可学习压缩}} +\gamma\,\underbrace{\lVert WW^\top-I\rVert_F^2}_{\text{正交正则}} } \tag{5}$

其中在带宽受限 ( $C_{\max}$ ) 场景，可把 $\beta$ 视作对链路费用的“物价系数”。

边缘推理机制：多视角注意力 ⊕ 回归–检索混合定位

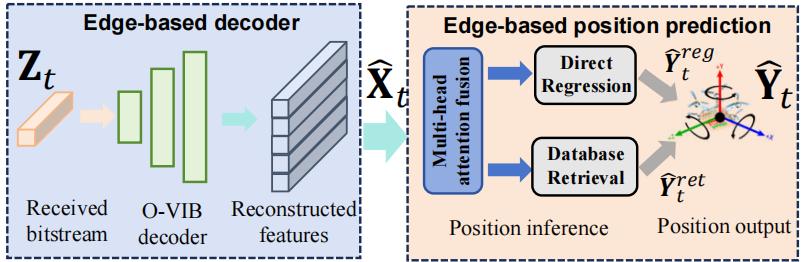
Decoder Architecture

压缩特征输入

五视角潜变量拼接为
$\mathbf Z_t=\bigl[\mathbf z_t^{(1)},\dots,\mathbf z_t^{(V)}\bigr]\in\mathbb R^{V\times d}, \quad V=5.$

多视角注意力融合

对每个视角嵌入施加线性投影得到
$\mathbf Q_t=\mathbf Z_tW_Q,\; \mathbf K_t=\mathbf Z_tW_K,\; \mathbf V_t=\mathbf Z_tW_V, \tag{6}$
其中 $W_Q,W_K,W_V\in\mathbb R^{d\times d_h}$ 。 Scaled Dot-Product Attention 计算权重
$\mathbf A_t=\operatorname{softmax}\!\Bigl(\frac{\mathbf Q_t\mathbf K_t^{\!\top}}{\sqrt{d_h}}\Bigr), \tag{7}$
融合特征为
$\mathbf f_t=\operatorname{Agg}\!\bigl(\mathbf A_t\mathbf V_t\bigr)\in\mathbb R^{d}, \tag{8}$
其中 $\operatorname{Agg}(\cdot)$ 可取均值或首行读取；多头情形将各头结果级联再经 FC 层得到 $\mathbf f_t$ 。

双路径位置推理

直接回归

$\widehat{\mathbf y}_t^{\,reg}=g_{\Theta_{reg}}\bigl(\mathbf f_t\bigr), \tag{9}$
$g_{\Theta_{reg}}$ 为 3-layer MLP，输出三自由度 $(x,y,\psi)$ 。同时回归分支预测对数方差 $\log\sigma_{reg}^2$ 作为置信度 $\kappa_{reg}=1/\sigma_{reg}^2$ 。

数据库检索

数据库 $\mathcal D=\{(\mathbf g_i,\mathbf y_i)\}_{i=1}^M$ 。计算与融合特征的余弦相似度
$s_i=\frac{\langle \mathbf f_t,\mathbf g_i\rangle}{\|\mathbf f_t\|\,\|\mathbf g_i\|},\quad w_i=\frac{e^{s_i}}{\sum_{j\in\mathcal N_k}e^{s_j}},\;i\in\mathcal N_k, \tag{10}$
其中 $\mathcal N_k$ 为相似度前 $k$ 个条目。检索位姿
$\widehat{\mathbf y}_t^{\,ret}=\sum_{i\in\mathcal N_k}\!w_i\,\mathbf y_i, \tag{11}$
并用相似度均值 $\bar s=\frac1k\sum_{i\in\mathcal N_k}s_i$ 给出置信度 $\kappa_{ret}=\bar s$ .

自适应权重融合

$\eta_t=\frac{\kappa_{reg}}{\kappa_{reg}+\kappa_{ret}},\qquad \widehat{\mathbf y}_t=\eta_t\,\widehat{\mathbf y}_t^{\,reg}+\bigl(1-\eta_t\bigr)\,\widehat{\mathbf y}_t^{\,ret}. \tag{12}$

当回归网络的方差小（ $\kappa_{reg}\!\uparrow$ ）且数据库相似度低，系统更信任回归；
反之，当收到高相似度检索结果时， $\eta_t\!\downarrow$ ，检索分支主导。

端到端训练目标

边缘端仅对回归输出反向传播
$\mathcal L_{loc}=\bigl\|\widehat{\mathbf y}_t^{\,reg}-\mathbf y_t\bigr\|^2, \tag{13}$
而检索路径参与推断不参与梯度；其相似度 $s_i$ 间接影响 $\eta_t$ ，从而影响合成输出。
最终系统与 UAV-侧编码器共同最小化
$\mathcal L_{total}=\lVert x-\hat x\rVert^2+\alpha\mathcal L_{loc} +\beta\, D_{\text{ARD}}(x) +\gamma \,\lVert WW^\top-I\rVert^2_F, \tag{14}$
利用任务为导向的通信方法实现“少发 ⊕ 准解”的通信–学习协同优化。

实验结果与部署评估

通信瓶颈vs传输延迟

特征尺寸vs定位误差

定位精度：在8KB/s下仍保持 < 10m 定位误差，比原始VIB降低 42.1%，比WebP编码器降 62.6%。
通信延迟：在4KB/s网络下，O-VIB延迟仅 240ms，远优于JPEG/H.264/WebP 等标准编码器（超过5秒）。
压缩效率：通过调整瓶颈因子 $\beta$ 和正交性权重 $\gamma$ ，在压缩率与准确度之间取得优雅权衡。

硬件实现

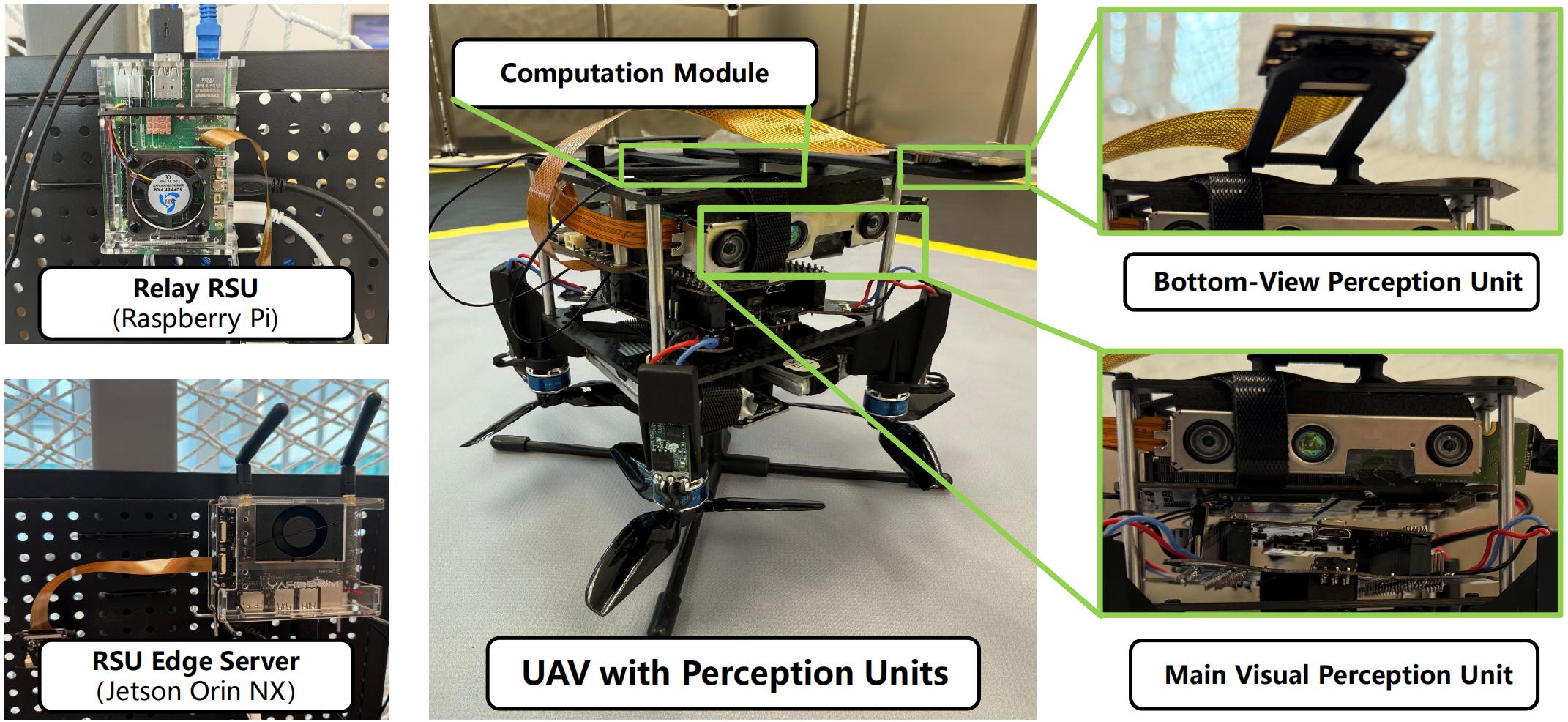
Hardware Setup
我们基于真实硬件搭建原型系统，以评估算法的编码解码复杂度与端到端时延：
无人机侧使用 Jetson Orin NX 8 GB 对五路相机流进行实时编码，并通过 IEEE 802.11 链路发送到附近的路侧单元（RSU）。前级 RSU（Raspberry Pi 5, 16 GB）负责初步转发，拥塞时通过千兆以太网将数据转发到云端边缘服务器；后级 RSU（Jetson Orin NX Super 16 GB）承担主干部位姿推理任务。该部署验证了 O-VIB 在实际带宽受限场景下（10 KB/s）依旧能够实现 <150 ms 的端到端延时与高精度定位。

Position Prediction Demo
绿点为真实位置（GT），红点为算法 Top-1 预测位置。

多视角无人机感知数据集介绍

Simulation Environment

平台搭建：基于 CARLA 仿真器与 Jetson Orin NX 真实部署；
数据规模：357,690 帧，覆盖 8 张城市地图；
视角配置：5 路摄像头同时采集 RGB / 深度 / 语义；
用途：用于研究在 GNSS 拒止场景下的视觉定位、通信优化。

Semantic Animation
对应帧的语义分割结果，可见行人、建筑、车辆等类别掩码。

Depth Animation
深度图示意，明暗表示近远距离。

数据集结构:

Dataset_CARLA/Dataset_all/
├── town01_20241217_215934.tar
├── town02_20241218_153549.tar
├── town03_20241217_222228.tar
├── town04_20241217_225428.tar
├── town05_20241218_092919.tar
├── town06_20241217_233050.tar
├── town07_20241218_153942.tar
└── town10hd_20241218_151215.tar

town05_20241218_092919/
├── calibration/
│   └── camera_calibration.json    # Contains parameters for all 5 UAV onboard cameras
├── depth/                         # Depth images from all cameras
│   ├── Back/
│   │   ├── 000000.npy             # Depth data in NumPy format
│   │   ├── 000000.png             # Visualization of depth data
│   │   └── ...
│   ├── Down/
│   ├── Front/
│   ├── Left/
│   └── Right/
├── metadata/                      # UAV position, rotation angles and timestamps
│   ├── 000000.json
│   ├── 000001.json
│   └── ...
├── rgb/                           # RGB images from all cameras (PNG format only)
│   ├── Back/
│   ├── Down/
│   ├── Front/
│   ├── Left/
│   └── Right/
└── semantic/                      # Semantic segmentation images (PNG format only)
    ├── Back/
    ├── Down/
    ├── Front/
    ├── Left/
    └── Right/