调和(级)数可以指跟约数和有关的整数欧尔调和数。在数学上,第n个调和数是首n个正整数的倒数和,即

它也等于这些自然数的调和平均值的倒数的 倍。它可以推广到正整数的倒数的幂之和,即
倍。它可以推广到正整数的倒数的幂之和,即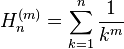 。
。
调和数的性质
根据定义,调和数满足递推关系
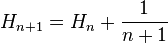
它也满足恒等式
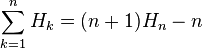
计算
对于第n项调和数,有以下公式

设: ,由此得到
,由此得到
对于调和数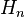 ,当n不是太大时,可以直接计算。
,当n不是太大时,可以直接计算。
当n特别大时,可以进行估算。
因为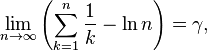
由此得到

当n越大时,估算越精确。
更精确的估算是

其中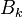 是第k项伯努利数。
是第k项伯努利数。
由估算看来,调和数是发散的,即: Hn 在n趋于无穷时没有极限
很早就有数学家研究,比如中世纪后期的数学家Oresme在1360年就证明了这个级数是发散的。他的方法很简单:
1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+...
1/2+1/2+(1/4+1/4)+(1/8+1/8+1/8+1/8)+...
注意后一个级数每一项对应的分数都小数调合级数中每一项,而且后面级数的括号中的数值和都为1/2,这样的1/2有无穷多个,所以后一个级数是趋向无穷大的,进而调合级数也是发散的。
广义调和数
广义调和数满足
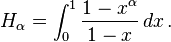
由此,我们得到
对于任意两个正整数p和q,并且p<q,我们有
微积分
对于每一个大于0的x,有

由此,得

对于每一个n,有

其他数列
根据定义,其他类似于调和数的数列有以下计算方法:
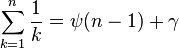
![\sum_{k=0}^n \frac{1}{2k + 1} = \frac{1}{2} \left[\psi \left(n + \frac{3}{2}\right) + \gamma \right] + \ln{2}](http://upload.wikimedia.org/math/e/9/6/e969bc0ecd3b1a0ac205247760f00633.png)
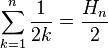







![\begin{align} H_n &= \int_0^1 \frac{1 - x^n}{1 - x}\,dx \\ &=-\int_1^0\frac{1-(1-u)^n}{u}\,du \\ &= \int_0^1\frac{1-(1-u)^n}{u}\,du \\ &= \int_0^1\left[\sum_{k=1}^n(-1)^{k-1}\binom nk u^{k-1}\right]\,du \\ &= \sum_{k=1}^n (-1)^{k-1}\binom nk \int_0^1u^{k-1}\,du \\ &= \sum_{k=1}^n(-1)^{k-1}\frac{1}{k}\binom nk . \end{align}](http://upload.wikimedia.org/math/d/7/e/d7e4e0ed50758b141c2cd4bfb4d6e3f4.png)
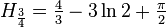


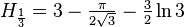
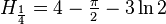

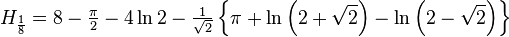

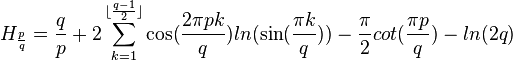














 770
770

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








