不规则多边形重心求解

一、不规则多边形重心求解

1.1 三角形重心计算方法

设三角形的三个顶点位置为$A(x_1,y_1)$,$B(x_2,y_2)$,$C(x_3,y_3)$，那么$△ABC$的重心$G$坐标为

$$x=\frac{x_1+x_2+x_3}{3},y=\frac{y_1+y_2+y_3}{3}$$

1.2 三角形面积计算方法

计算三角形的面积使用向量积的方式，下图中，假设P点为原点，$A(x_1,y_1)$，$B(x_2,y_2)$。

以$A$，$B$和坐标原点$P$构成的$△ABC$的面积为
$$S=\frac{\overrightarrow{PB}\times \overrightarrow{PA}}{2}=\frac{x_2{y}_1-x_1{y}_2}{2}$$

1.3 多边形面积的计算方法

对于多边形的情况，我们可以将多边形切分为多个三角形，分别进行求解。那么这个剖分点$ P$ 我们可以设在哪里呢？这里先给出结论：这个剖分点可以设置在多边形的内部，也可以设置到外部。

为什么这个剖分点可以设置到外部呢？我们可以通过简单的三角形情况来推广到多边形的情况。 对于$△ABC$，我们把剖分点设置在其外部$ P$ 的一点上，

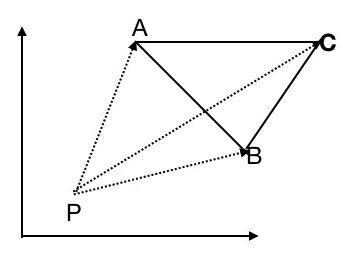
$△ABC$的面积$S$为
$$S=\frac{1}{2}(\overrightarrow{PB}\times \overrightarrow{PC}+\overrightarrow{PC}\times \overrightarrow{PA}+\overrightarrow{PA}\times \overrightarrow{PB})$$
设$P(x_0,y_0),$$A(x_1,y_1)$,$B(x_2,y_2)$,$C(x_3,y_3)$

$△ABC$的面积$S$可以写为
$$S=\frac{1}{2}\left(x_1{y}_2-x_2{y}_1+x_2{y}_3-x_3{y}_2+x_3{y}_1-x_1{y}_3\right)$$

这时可以发现跟外部点$P$没有关系，只跟顶点的坐标有关系。

1.4 不规则多边形的重心计算方法

不规则图形一般没有中心点这个概念，所以只能使用重心来代替中心点，这里先给出一个公式：

平面多边形$X$可以被剖分为$n$个有限的简单图形$X_1,X_2,\dots ,X_n$，这些简单图形的重心点为$G_i$，面积为$S_i$，那么这个平面多边形的重心点坐标$G(x,y)$为
$$x=\frac{{\sum }_n^{i=1}{G}_{ix}{S}_i}{{\sum }_{i=1}^n{S}_i},y=\frac{{\sum }_n^{i=1}{G}_{iy}{S}_i}{{\sum }_{i=1}^n{S}_i}$$

• 不规则多边形重心计算

def get_gravity_point(points):
    """
    @brief      获取多边形的重心点
    @param      points  The points
    @return     The center of gravity point.
    """
    if len(points) <= 2:
        return list()

    area = Decimal(0.0)
    x, y = Decimal(0.0), Decimal(0.0)
    for i in range(len(points)):
        lng = Decimal(points[i][0])
        lat = Decimal(points[i][1])
        nextlng = Decimal(points[i-1][0])
        nextlat = Decimal(points[i-1][1])

        tmp_area = (nextlng*lat - nextlat*lng)/Decimal(2.0)
        area += tmp_area
        x += tmp_area*(lng+nextlng)/Decimal(3.0)
        y += tmp_area*(lat+nextlat)/Decimal(3.0)
    x = x/area
    y = y/area
    return [float(x), float(y)]