交互式分割-Intelligent Scissors 问题总结

以下内容是对下面几篇文章的学习总结:

https://blog.csdn.net/mapupcal/article/details/80030643#to_do

https://blog.csdn.net/mahabharata_/article/details/69099136

https://blog.csdn.net/DdogYuan/article/details/80554873

前言

      智能剪刀算法（Intelligent Scissors）是由Eric N. Mortensen和William A. Barrett于1995年提出来的一种图像分割的交互算法，可以用于2D图像分割，该算法可以用于辅助用户精确地勾勒出感兴趣的区域。在运行时它快速地定位到该图像区域的边缘上，通过与用户交互，更精确地完成整个感兴趣区域的勾画、分割。

论文地址:

Intelligent Scissors for Image Composition

https://courses.cs.washington.edu/courses/csep576/15sp/readings/mort-sigg95.pdf

Interactive segmentation with intelligent scissors

https://www.sciencedirect.com/science/article/pii/S1077316998904804/pdf?md5=8d394efbaeb90a1e70218b4d156fa34b&pid=1-s2.0-S1077316998904804-main.pdf

 

效果：(图片来自论文)

算法原理

要点：

①将图像转换成一个庞大的加权有向图。

②在运行时，通过特定的寻路算法，在出发点[a]开始，寻找一条最优路径，该路径通往用户指定的目标点[b]。

将图像变成一个庞大的加权有向图：

① 图像中每个像素，在加权有向图中都将成为该图中的一个结点Node。

② 相邻的像素，互相之间存在一条加权有向边。

③ 确定每条加权有向边的权重。

前提设定

初始点（seedpoint）

对于下文中所有用到的p与q的意义：

p表示图中的中心结点，q指与p相邻的结点。

对于某一个非边界像素p,其有八个邻居像素，如：

 

当转换成加权有向图之后，就变成如下这个样子：

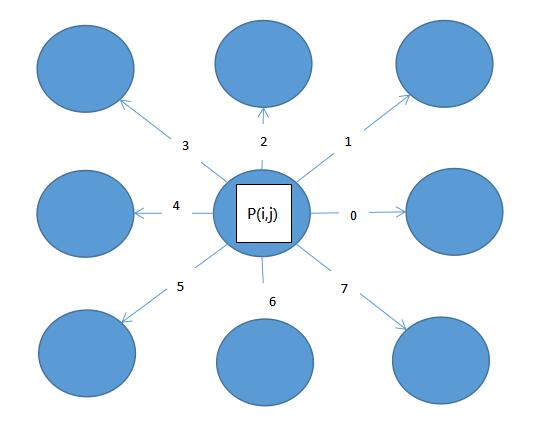
上图中的3，2，1，4，0，7，5，6，7表示的是对应的邻域到seed point的代价，需要注意的是，我们在计算过程会得到邻域到seed point的local host（下文会详细介绍local host），如下图所示，q像素点上的值表示它到p像素点的local host。

   图1-local host

           图2-代价

对比图一与图二，我们可以知道，邻域到seed point的local host 与邻域到seed point的代价之间的转换关系是：

1.seed point本身的local cost（图1中的2）没有任何作用

2.邻域到seed point的代价不是local costs相减，如果是正左/右/上/下 方的点，邻域到seed point的代价=邻域到seed point的local host（如图中正右方的点到seed point的代价为1），如果是就是对角线上的像素，邻域到seed point的代价=根号2*邻域到seed point的local host

下文中公式用到的符号：

拉普拉斯交叉零点值 Fz(q)

像素点梯度值 Fg(q)

像素点梯度方向 Fd(p,q)

像素值    Fp(q)

“内部”像素值    Fi(q)

“外部”像素值    Fo(q)
 

论文的思路：

论文中的代价与边缘特征有关，边缘特征越明显的像素点，代价越低，所以我们要通过计算代价，去找最小代价路径，这样便使得最小代价路径总是会去“贴合”图像的边缘。

那么论文中的代价是怎么定义的呢？

注:以下只介绍第一篇论文中的local costs描述，在第二篇中作者又考虑了另外三项，有兴趣的读者可以自行阅读

代价Local Costs描述

我们称之前提到的代价为local costs，论文一中，Local Costs由三个图像特征组成

local costs通过这三个Image Feature的权重合得到：

其中最为重要的是fG，即图像的梯度幅值。

fG的实现

设图像像素坐标为(x,y)处的梯度幅值为M(x,y)，有：

使用sobleFilter，其最小的3X3模版使用以z5为中心的一个3X3领域对gx和gy的近似如下式所示：

梯度幅值越大，意味着具有更多的边缘特征，在前面的建模中提到边缘特征意味着路径代价低，故f(G)应该这样设置：

实现了fG之后就可以看到明显的效果，建议先实现f(G)再慢慢补充fZ和fD。fZ和fD的具体实现可以参考论文，其作用分别是使得曲线更加贴合边缘和更加平滑。

fZ的实现

意义

fZ是拉普拉斯零交（Laplacian Zero-Crossing）带来的代价，拉普拉斯算子的卷积就是原图像素二维导数，表示的图像一维导数变化的速率。拉普拉斯算子卷积为0的地方意味着该点是一维导数变化的极值点，其变化速率最快，我们认为这是边缘的特征，故其代价应该较低。我们将拉普拉斯算子卷积为0的地方的代价设为0，不为0的地方设为1。

特殊处理

由于拉普拉斯算子卷积刚好为0的地方极少，所以我们需要特殊处理以增多代价为0的点。
我们认为，当两个临近像素出现异号时，其中间肯定有卷积为0的位置，但是由于像素是离散的，我们设卷积值离0近的像素的代价为0，这样就增多了代价为0的点，使得拉普拉斯零交特征的影响增大。

fD的实现

意义
fD是为了使得边缘平滑，实现平滑的方式是通过为剧烈变化的边界方向设置较高的代价。

实现方法
设D（p）为某个像素点的梯度方向(Ix,Iy)，其中Ix和Iy分别为图像在x方向和y方向上的梯度，D’（p）为(Iy,-Ix)，与D（p）正交。设L(p,q)为p到q的单位向量。fD的详尽计算公式参考论文。

示例如下

算法流程描述

（a）

下图(a)描述了各个像素点的local costs，(a)中画圈的local cost为2的像素点代表着seed point，设其为S
设置seed point后，计算图像所有像素到该点的代价，其过程如(b) （c） (d)所示：

(b)

第一步，计算S的邻域（8个像素点）到S的代价，注意对照(a)，S本身的local cost为2没有任何作用，因为S到自身的代价为0（这不是废话嘛。。。），邻域到S的代价不是local costs相减（例如S的左边像素自身的local costs为4，它到S的代价不是4-2，而是4），还有就是对角线上的像素到S的代价是其自身的local cost乘上了根号2，这是因为对角线的长度比直线长度长。

(c)

第二步，选取当前代价最低的路径（回忆Dijkstra算法）(a)中此时的路径只有其邻域到S的路径，其右方邻域像素N1到S的代价最低，标记N1：它要到达seed point，就走它的左邻域，这样可以使得总代价最小。
其中，N1的代价指的是便是N1到seed point的代价和。
然后计算N1的邻域到N1的代价，N1的邻域的代价不仅仅是其local cost的值，还要加上N1自身的代价（这样才是总代价）。观察下(b)图中S的右上方邻域像素（其 local cost为11）N2，对照©，发现其箭头指向了N1，并且其代价值更新为了9，这是因为在第二步中，计算得到N2的代价为8+1 = 9，它比原来8*根号2 = 11要小，故需要进行更新。
更新意味着，N2此时知道自己要去到seed point的最小代价路径是走下方而不是左下方直接去seed point，这里也需要一个标记动作。（类似前面标记N1）

一次expand

以上两步可以称为一次expand
下一次expand也是类似，选取当前代价最低的路径，例如下一次expand应该选取的是S的上方像素（可以看到，是从全局来选取）