版权声明:本文为博主原创文章,未经博主允许不得转载。https://mp.csdn.net/mdeditor/89682552
本文将介绍遗传算法概念、算法中名词、算法的实现过程以及附上解决旅行商问题的GA的MATLAB代码。
1.遗传算法(Genetic algorithm,GA)介绍
(1)概念:遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法;换种说法:是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
(2)由来:它是由美国的J.Holland教授1975年首先提出,其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。
(3)应用领域:广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域,主要还是解决优化类问题。
(4)相关名词:
1)种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
2)个体:组成种群的单个生物。
3)基因 ( Gene ) :一个遗传因子。
4)染色体 ( Chromosome ) :包含一组的基因。
5)适应度函数(生存竞争-对于个体间,适者生存-对应于自然):对环境适应度高的个体参与繁殖的机会比较多,后代就会越来越多。适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
6)遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
(总结:繁殖过程,会发生基因交叉( Crossover ) ,基因突变 ( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。)
(5)算法思想:借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。这样进化N代后就很有可能会进化出适应度函数值很高的个体。
2.旅行商问题介绍
问题:旅行商问题(Traveling Salesman Problem,TSP),是数学领域中著名问题之一。这个问题是这样的:假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径长度为所有路径之中的最小值。TSP是一个典型的组合优化问题,且是一个NP完全难题(NP完全问题(NP-C问题),是世界七大数学难题之一。 NP的英文全称是Non-deterministic Polynomial的问题,即多项式复杂程度的非确定性问题。),关于NP的这个概念本文就不做详细介绍了,但简单的说就是:TSP问题目前尚不能找到一个多项式时间复杂度的算法来求解,它的开销很大。
问题的关键不在于寻找两两城市间的最短路径,而在于去寻找一那条最短的巡回路径,换句话说,就是寻找一组拜访城市的先后次序序列
分析:所以该怎么求解呢,我们很容易想到一种类似于穷举的思路:现在假设我们要拜访10个城市,从城市1出发,最后回到城市1。显然,从城市1出来后,我们随即可以选择剩余的9个城市之一进行拜访(这里所有城市都是连通的,总是可达的,而不连通的情况属于个人特殊业务的装饰处理,不是本文考虑范畴),那么很显然这里就有9种选择,以此类推,下一次就有8种选择…总的可选路线数就是:9!。也就是说需要用for循环迭代9!次,才能找出所有的路线,进而筛选出最短的那条来。如果只拜访个10个城市或许还好的话(需要迭代9!次),那要拜访100个城市(需要迭代9.3326215443944 * 10^157)简直就是计算机的噩梦!更多个城市的话,计算的时间开销可想而知!
更一般地,如果要拜访n+1个城市,总的可选路线数就是n!,进而时间复杂度就是O(n!),从这里我们同理也可以看出,这个算法的时间复杂度是非多项式的,它的开销大是显而易见的。所以问题的关键不在于寻找两两城市间的最短路径,而在于去寻找一那条最短的巡回路径,换句话说,就是寻找一组拜访城市的先后次序序列。
(以上部分摘自作者:阿堃堃堃堃,链接:https://www.jianshu.com/p/478f6b1fe60f,来源:简书)
3.GA实现步骤
然后,既然已知问题所在,在GA简单介绍后,我们进一步探索GA实现的具体算法流程。
(1)初始化参数:比如种群规模,个体数量、变异概率、交叉概率适应度函数、以及迭代次数等;
(2)确定种群和个体,比如旅行商问题中是这样的一个城市群有多少个城市以及假如某个国家有多少个差不多这样的城市群。旅行商问题中我们要确定的是城市的初始坐标(这个可以随机产生也可代入具体城市坐标数值),之后是整个城市群坐标集合(当然也可理想化处理有助于简化数学模型简化建模和计算);
(3)生成种群对应的适应度函数;
(4)交叉和变异:就是群体中单个点变异;交叉就是种群中随机两个个体随机交换部分内容;
(5)选择(这也是优胜劣汰自然选择的一种评价指标)问题:
*
4.GA代码
function main()
clear all;clc;close all;
%% 1.参数初始化
N=18; %城市的个数
M=100; %种群的个数
C=500; %迭代次数
m=2; %适应值归一化淘汰加速指数
Pc=0.5; %交叉概率
Pmutation=0.2; %变异概率
pos=10*randn(N,2); %生成城市的坐标
D=zeros(N,N); %生成城市之间距离矩阵
%计算两点间的距离
for i=1:N
for j=i+1:N
dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
D(i,j)=dis^(0.5);
D(j,i)=D(i,j);
end
end
%% 2.1生成初始群体
popm=zeros(M,N);
for i=1:M
popm(i,:)=randperm(N); %将N序号随机打乱
end
%%2.2随机选择一个种群
R=popm(1,:);
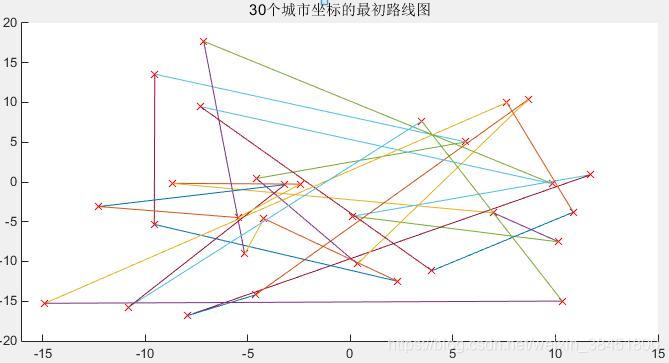
figure(1);
scatter(pos(:,1),pos(:,2),'ro');
plot_route(pos,R); %画出种群各城市之间的连线
axis([-20 30 -20 30]);
title('18个城市坐标的最初路线图');
str=['初代,','总距离:',num2str(dis)];
text(1000,5000,str);
%% 3.初始化种群及其适应函数
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);
minlen=min(len);
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
R=popm(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
fitness=fitness/sum(fitness);
distance_min=zeros(C+1,1); %%各次迭代的最小的种群的距离
while C>=0
fprintf('迭代第%d次\n',C);
%%选择操作
nn=0;
for i=1:size(popm,1)
len_1(i,1)=myLength(D,popm(i,:));
jc=rand*0.3;
for j=1:size(popm,1)
if fitness(j,1)>=jc
nn=nn+1;
popm_sel(nn,:)=popm(j,:);
break;
end
end
end
%%每次选择都保存最优的种群
popm_sel=popm_sel(1:nn,:);
[len_m len_index]=min(len_1);
popm_sel=[popm_sel;popm(len_index,:)];
%%交叉操作
nnper=randperm(nn);
A=popm_sel(nnper(1),:);
B=popm_sel(nnper(2),:);
for i=1:nn*Pc
[A,B]=cross(A,B);
popm_sel(nnper(1),:)=A;
popm_sel(nnper(2),:)=B;
end
%%变异操作
for i=1:nn
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
end
end
%%求适应度函数
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(C+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf('minlen=%d\n',minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
popm=[];
popm=popm_sel;
C=C-1;
%pause(1);
end
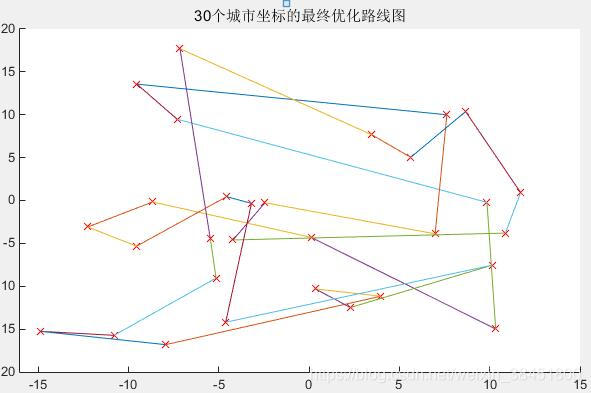
figure(2)
plot_route(pos,R);
axis([-20 30 -20 30]);
title('38个城市坐标的最终优化路线图');
str=['初代,','总距离:',num2str(dis)];
text(1000,5000,str);
end
%% 城市点间连线
function plot_route(a,R)
scatter(a(:,1),a(:,2),'rx');
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
x0=a(R(i-1),1);
y0=a(R(i-1),2);
x1=a(R(i),1);
y1=a(R(i),2);
xx=[x0,x1];
yy=[y0,y1];
plot(xx,yy);
hold on;
end
end
%% 个体距离计算函数 mylength.m
function len=myLength(D,p)
[N,NN]=size(D);
len=D(p(1,N),p(1,1));
for i=1:(N-1)
len=len+D(p(1,i),p(1,i+1));
end
end
%% 适应度函数fit.m
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i =1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end
end
%% 交叉操作函数 cross.m
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
p=unidrnd(L-W+1);
fprintf('p=%d ',p);
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end
%% 对调函数 exchange.m
function [x,y]=exchange(x,y)
temp=x;
x=y;
y=temp;
end
%% 变异函数 Mutation.m
function a=Mutation(A)
index1=0;
index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;
end
小结: 以上还有很多不完善的,会进一步后期添加内容,使GA更加通俗易懂的呈现给大家。


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










