HoudiniVex笔记_P15_MatrixBasics矩阵基础

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5    如有错误，请指正，Thansks.

原理推导略微复杂，非必要不要去深究。感兴趣的可以去看看线性代数-UP主汉语配音-【线性代数的本质】合集-转载于3Blue1Brown官方双语】_哔哩哔哩_bilibili

1、矩阵类型

Houdini中有三种矩阵类型：2x2矩阵(2D旋转)、3X3矩阵(3D旋转)、4X4矩阵(平移、旋转、缩放)，

eg.可在类型为detail的AttributeWrangle节点输入以下代码，创建不同的矩阵：

matrix2 mat2 = set(1,2,3,4);
matrix3 mat3 = set(1,2,3,4,5,6,7,8,9);
matrix mat4 = set(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16);

2@mat2 = mat2;
3@mat3 = mat3;
4@mat4 = mat4;

 结果为：

2、矩阵声明

使用大括号  {    }  时不能使用变量。

eg.可在类型为detail的AttributeWrangle节点输入以下代码，体验矩阵声明的方法：

float val = 1.0;

matrix mat1 = set(val,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16);
matrix mat2 = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
matrix mat3 = {{1,2,3,4},{5,6,7,8},{9,10,11,12},{13,14,15,16}};
matrix mat4 = set(set(val,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));

4@mat1 = mat1;
4@mat2 = mat2;
4@mat3 = mat3;
4@mat4 = mat4;

结果：

3、单位矩阵

单位矩阵：仅对角线为1 ，其它为0，它的值=1。

 eg.可在类型为detail的AttributeWrangle节点输入以下代码创建单位矩阵：

matrix2 mat2 = ident();
matrix3 mat3 = ident();
matrix mat4 = ident();

2@mat2 = mat2;
3@mat3 = mat3;
4@mat = mat4;

结果为：

4、行列式与逆矩阵

①2x2矩阵，用下面公式计算它的值，

如果值=0，表示该矩阵无逆矩阵，如≠0，表示该矩阵有逆矩阵。
矩阵与逆矩阵相乘，等于单位矩阵，

②3x3矩阵，可用下面方法计算它的行列式值，即对角线上的元素相乘，红色相加的和 减去 蓝色相加的和，

 ③4X4矩阵与3x3矩阵相似。

eg.逆矩阵函数 invert(matrix) 、行列式计算函数determinant(matrix)：

 可在类型为detail的AttributeWrangle节点输入以下代码，体验逆矩阵函数、行列式函数，

matrix mat = set(set(1,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));
matrix imat = invert(mat);      //转为逆矩阵

float det = determinant(mat);   //矩阵行列式值

matrix mat2 = set(set(3,2,3,20),set(5,11,7,8),set(9,10,11,12),set(3,14,15,16));
matrix imat2 = invert(mat2);    //转为逆矩阵

float det2 = determinant(mat2); //矩阵行列式值

f@det = det;                    //如果值为0，该矩阵没有逆矩阵
f@det2 = det2;                  //如果值不为0，该矩阵有逆矩阵

matrix cmat = mat * imat;       //矩阵与逆矩阵相乘
4@cmat = cmat;

matrix cmat2 = mat2 * imat2;    //矩阵与逆矩阵相乘
4@cmat2 = cmat2;                //值接近单位矩阵

5、转置矩阵

将矩阵的行、列置换得到新的矩阵，即转置矩阵。常用于投影…等更复杂的转换。

对矩阵A进行转置，可得：如下图所示

转置矩阵的性质：和、点乘、逆矩阵
 

eg.可在类型为detail的AttributeWrangle节点输入以下代码，

matrix mat = set(set(1,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));

4@mat = mat;

4@tmat = transpose(mat);    //将矩阵行列置换

 结果为：

6.、矩阵与标量乘法运算

矩阵乘法主要有3种，矩阵与标量(float)相乘、矩阵与矩阵相乘、矩阵与向量相乘。

下面是Multiplication  with Saclar与标量相乘：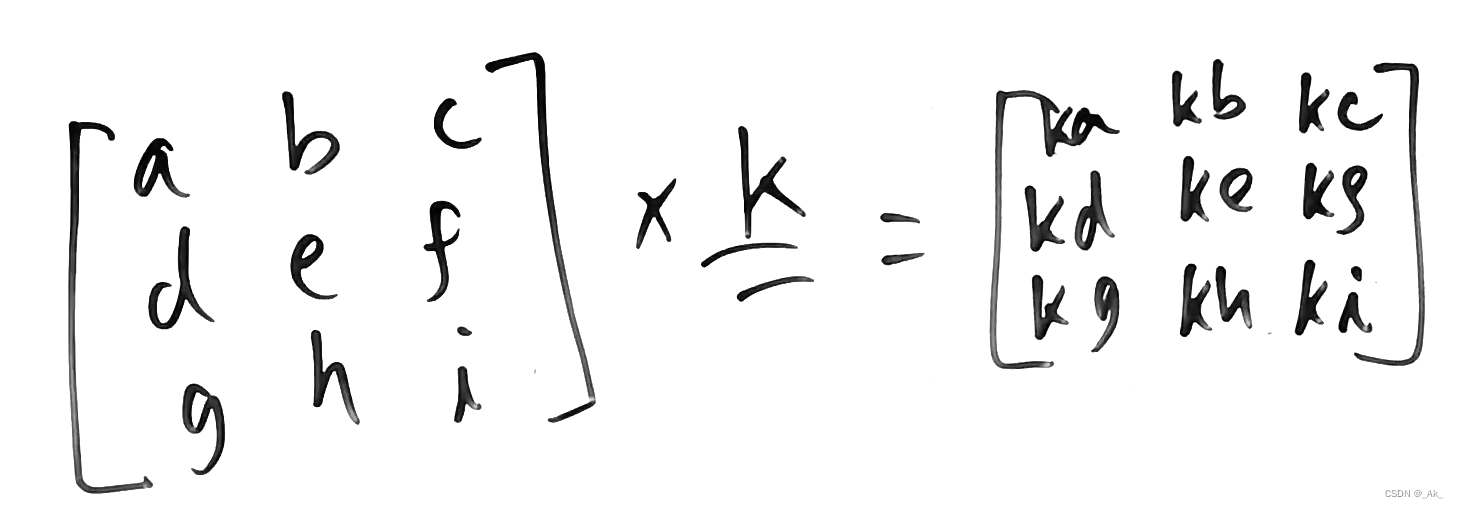

eg.可在类型为detail的AttributeWrangle节点输入以下代码，

matrix mat = set(set(1,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));

mat = mat * 2.0;      //  mat = mat * chf('num');

4@mat = mat;    //结果：略

7、与矩阵相乘

如前所述，矩阵包含位置、旋转、缩放等信息，相乘顺序不同，结果也不同。因为在移动、旋转、缩放的变换中，物体变换中心点是以(0, 0, 0)为变换中心，懂？（在Houdini中，矩阵与向量相乘，顺序不影响结果）。

①相同行列矩阵相乘：

②非相同行列矩阵相乘，左边矩阵行数为新矩阵行数，右边矩阵列数为新矩阵列数；

在Houdini中，2x3矩阵、3x2矩阵没有任何函数或定义，仅作理解

 
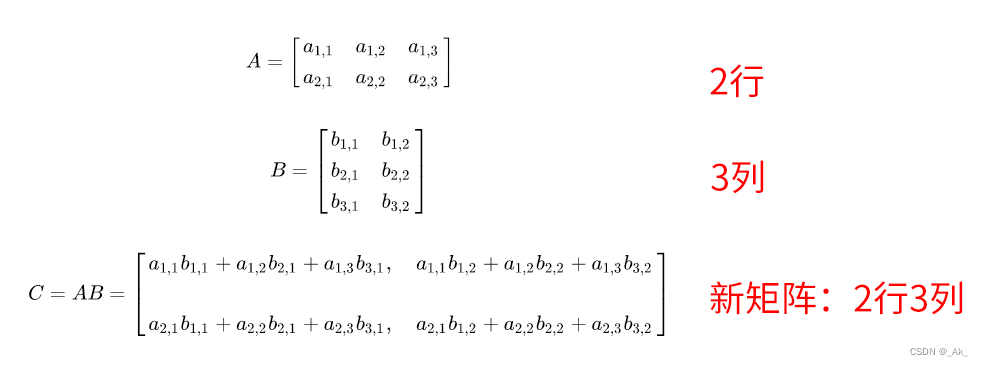
用这图应该更易理解些：

eg.可在类型为detail的AttributeWrangle节点输入以下代码，

matrix mat1 = set(set(1,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));
matrix mat2 = set(set(16,15,14,13),set(12,11,10,9),set(8,7,6,5),set(4,3,2,1));

matrix mat3 = mat1 * mat2;       //相乘顺序不同 结果不同
matrix mat4 = mat2 * mat1;   

4@mat3 = mat3;
4@mat4 = mat4;

 结果为： //相乘顺序不同 结果不同，

8、与单位矩阵相乘

矩阵与单位矩阵相乘，得到的还是原矩阵，相乘顺序不影响结果。

9、与转置矩阵相乘

矩阵与转置矩阵相乘：

eg.可在类型为detail的AttributeWrangle节点输入以下代码，

matrix mat1 = set(set(1,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));
matrix mat2 = set(set(16,15,14,13),set(12,11,10,9),set(8,7,6,5),set(4,3,2,1));

matrix mat3 = transpose(mat1) * transpose(mat2);   
matrix mat4 = transpose(mat2 * mat1);   

4@mat3 = mat3;
4@mat4 = mat4;

 结果为：两结果相同

10、与向量相乘

①行向量与矩阵相乘，得到一个新向量/值。一般来说，使用向量时需要注意顺序，但是在Houdini中，向量与矩阵相乘，顺序不影响结果，

或者：

eg.可在类型为detail的AttributeWrangle节点输入以下代码，

//向量与矩阵相乘 顺序不影响结果
vector v = set(1, 2, 3);

matrix mat = set(set(1,2,3,4),set(5,6,7,8),set(9,10,11,12),set(13,14,15,16));

vector v1 = v * mat;
vector v2 = mat * v;

v@v1 = v1;
v@v2 = v2;    //    v1 与 v2 结果相等

 ②矩阵与列向量相乘，得到一个新矩阵（2行1列）

③4X4矩阵与向量相乘
与上面的【①行向量与矩阵相乘】相似，只不过在与4X4矩阵相乘的过程中，向量 (x, y, z) 被转换成  (x, y, z, 1) 后再与4X4矩阵相乘。
(x, y, z, 1) ：参数1表示位置/移动、参数为0时表示方向，不写参数默认为1/位置。

11、矩阵与位移

在4x4矩阵中，最后一行表示位移Translation值。
比如，某物体从点 (x, y, z) 移动到某点，即移动向量 (a, b, c)， 把向量带入到4X4矩阵，移动后的新位置为：

当然，单一移动使用矩阵意义不大。需要复杂变换时可使用矩阵进行变换。
eg.一个polygon的Sphere小球节点、一个类型为Points的AttributeWrangle节点输入以下代码：

vector move = chv('move');    //向量通道

matrix mat = ident();        //单位向量
translate(mat, move);        //移动

@P = @P * mat;        //小球移动
    
// @P = @P + move;        用这也可以达到同样的移动效果

结果：滑动通道向量move值，小球根据向量值移动。

12、矩阵与缩放

物体的每个坐标的x、y、z值具有特定大小或特定比例值，假设物体某个点位置为 (x, y, z) ，按比例 (a, b, c) 进行缩放，那么该点的新位置为 (ax, by, cz)，在矩阵中可表示为：

 当然，单一缩放使用矩阵意义不大。需要复杂变换时可使用矩阵进行变换。
eg.一个polygon的Sphere小球节点、一个类型为Points的AttributeWrangle节点输入以下代码：

vector scale = chv('scale');    //向量通道

matrix mat = ident();           //单位矩阵
scale(mat, scale);          //使用矩阵进行缩放

@P = @P * mat;              //小球缩放 

// @P = @P * scale;      用这也可以达到同样的缩放效果

结果：滑动向量通道的x、y、z值，可以控制小球的x、y、z方向的缩放。

13、矩阵与旋转

以2D旋转为例，在二维空间中的任意向量，可以通过二维的基向量来表示向量（可以理解为用坐标系来表示）。可以联想一下物理中的静止参考系和动参考系。动静参考系在这里对应于动静坐标系。向量旋转的同时，动坐标系是相对于这个向量不动的，相对于静止坐标系则旋转同样的角度。只要知道旋转后动坐标系中的标准正交基在静止坐标系中的表达，就能知道旋转后的向量在静止坐标系中的表达。（本段文字来自@太阳与风博士）

向量绕二维直角坐标系原点逆时针旋转θ，对应的旋转矩阵R(θ)为：

 关于2X2旋转矩阵的推导过程，及3x3旋转矩阵可以看这里的推导过程，点击直达。

eg.按下图添加节点，

在类型为points的rotate中写入以下代码：

vector axis = normalize(point(1, 'P', 1));  //直线作为旋转轴
float ang = radians(chf('angle'));          //范围设为0~360

matrix mat = ident();       //单位矩阵

rotate(mat, ang, axis);     //旋转，直线为旋转轴，旋转角度为ang

@P *= mat;                  //更新box位置          

 结果：改变直线转向及滑动角度ang值，box仍以直线为旋转轴进行旋转。

14、组合变换矩阵

移动、旋转、缩放组合变换，看看不同顺序的组合变化。

（理论可以大概参考这篇文章——>点击直达）

eg.一个box盒子节点、一个类型为Points的AttributeWrangle节点输入以下代码：

matrix mat = ident();

float ang = radians(chf('angle'));      //设置范围0~360
vector axis = set(0, 1, 0);             //旋转轴
vector move = set(chf('move'), 1, 1);   //暂设置为1~3
vector scale = set(chf('scale'), 1, 1); //暂设置为0-3

//改变下面三行代码的顺序，变换结果不相同
translate(mat, move);
scale(mat, scale);
rotate(mat, ang, axis);

@P *= mat;

结果：略

如何确定变换顺序？

使用 maletransform()函数， 可在Houdini自带的外部脚本处查看具体用法（安装路径\houdini\vex\include\math.h），下面使用记事本打开math.h脚本，

 如图所示，可以使用【XFORM_SRT】或【XFORM_0】等确定组合变换顺序。（截图后半部分是四元数相关的欧拉角转换顺序）。

eg.对上面的【eg】代码进行修改，

float ang = chf('angle');      //旋转角度 设置范围0~360
vector rot = set(0, ang, 0);             //沿Y轴旋转角度
vector move = set(chf('move'), 0, 0);   //暂设置为1~3
vector scale = set(chf('scale'), 1, 1); //暂设置为0-3

int trs = chi('trs');       //位移、旋转、缩放变换顺序，范围0~5
int xyz = chi('xyz');       //旋转顺序，范围0~5

matrix mat = maketransform(trs, xyz, move, rot, scale);

@P *= mat;

结果：略

15、矩阵转换函数

cracktransform() 函数把4x4矩阵分解为位移、旋转、缩放。

使用该函数，必须知道/指定变换顺序、转换顺序

eg.使用【14、Combine Transformation Matrix组合变换矩阵】的节点及代码，
①在代码节点最后一行加上一行代码，

4@mat = mat;

②添加并在下方连接类型为points的attributeWrangle节点，并写入以下代码，

int trs = chi('trs');    //与上一节点的 trs 复制粘贴相对引用
int xyz = chi('xyz');    //与上一节点的 xyz 复制粘贴相对引用

vector t, r, s;
cracktransform(trs, xyz, set(0, 0, 0), 4@mat, t, r, s);

v@t = t;
v@r = r;
v@s = s;

结果：略

16、小练1—基础变换

eg.一个box盒子节点、一个类型为Points的AttributeWrangle节点输入以下代码：

float rad = chf('rad');                 //后面用作在X轴上的位移距离
float ang = radians(chf('ang'));        //旋转角度  范围设置0~360
        
float size = cos(ang * 4);              //一个360°周期内，进行了4次变换
size = fit(size, -1, 1, 1.0, 3.0);      //映射函数，把size值从-1到1重新映射为1.0到3.0

matrix mat = ident();
translate(mat, set(0.5, 0, 0));         //设置中心点，因为box默认中心点为(0,0,0)且默认大小为1
scale(mat, set(size, 1, 1));            //X方向进行缩放
translate(mat, set(rad, 0, 0));         //在X轴上的位移
rotate(mat, ang, set(0, 0, 1));         //旋转角度，即转1圈

@P *= mat;

结果：①滑动rad值；②在生成的通道中，把ang通道值改为：$FF / $FEND * 360，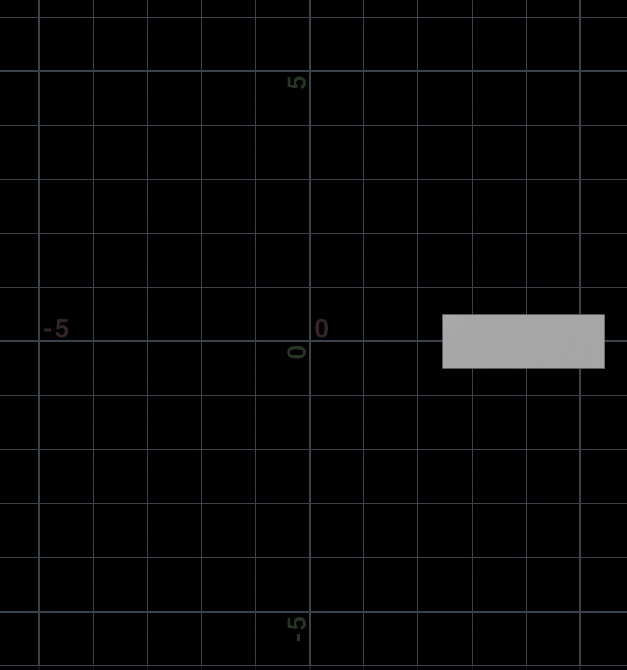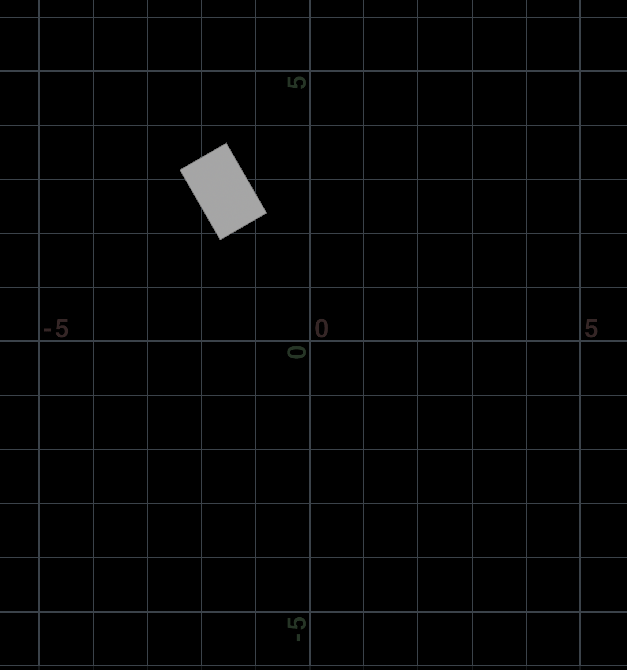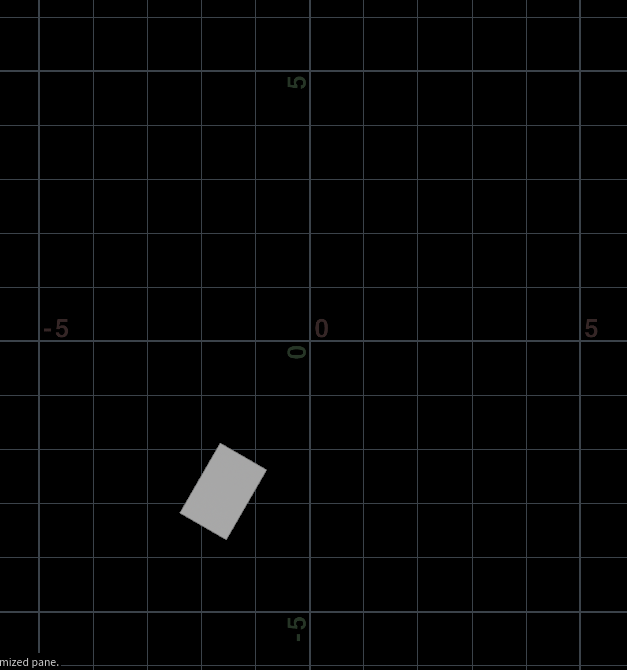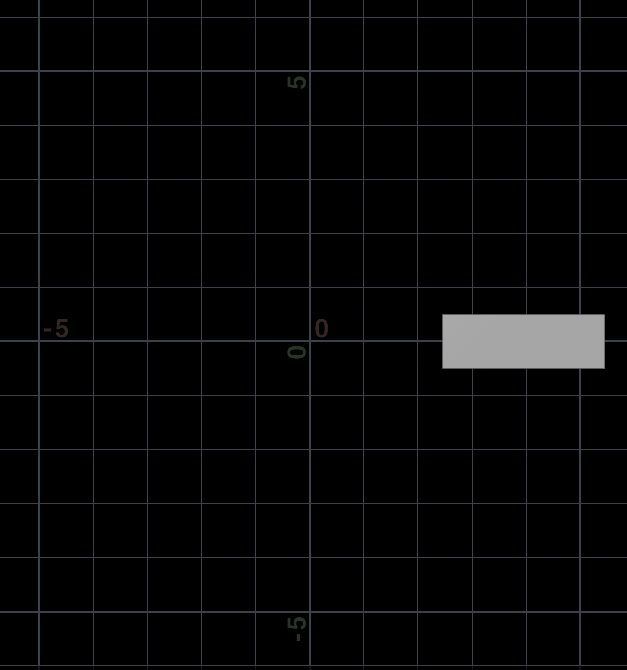

17、小练2—扭曲和弯曲

eg.①一个box盒子节点、一个类型为Points的AttributeWrangle节点输入以下代码：

float boxheight = chf('boxheight');         //box高度，与box节点的Y轴高度【复制-粘贴引用】
float twistang = chf('twist_ang') * $PI;    //扭曲角度
float bendrad = chf('bend_rad');
float bendang = chf('bend_ang') * $PI;

matrix mat = ident();

//根据box的高度/Y轴坐标值映射为角度范围 (0.0, twistang)。因为box中心点在 (0,0,0)，所以需要乘以0.5
float tang = fit(@P.y, -boxheight * 0.5, boxheight * 0.5, 0.0, twistang);   
rotate(mat, tang, set(0, 1, 0));        // 得到一个旋转矩阵，以Y轴为轴心旋转，旋转角度 0~tang°
//scale值为0.01~1.0~0.01   根据box的高度/Y轴坐标值映射为0.0~180°，角度范围对应sin函数值范围为0~1~0

float scale = max(sin(fit(@P.y, -boxheight * 0.5, boxheight * 0.5, 0.0, $PI)), 0.01);    
scale(mat, set(scale, 1, scale));     //位于X、Y轴的点进行缩放，缩放为 0.01 ~ 1 ~ 0.01

@P *= mat;

其中一些设置：box节点的细分设置为(5,50,5)，高度设置为5(大小随意)；AttributeWrangle节点的boxheight通道设置为：与box的高度绑定，即【复制-粘贴引用】，

结果为：基于上述条件，及twist_ang=1.5的情况下，(为了排版美观，下图旋转90°为正确结果)

 ②对代码进行添加弯曲代码，完整代码如下，

float boxheight = chf('boxheight');         
float twistang = chf('twist_ang') * $PI;   

//添加代码
float bendrad = chf('bend_rad');            //弯曲半径/移动距离
float bendang = chf('bend_ang') * $PI;      //弯曲角度  范围暂设为0~2，即最大值为2π，即一个圆

matrix mat = ident();

float tang = fit(@P.y, -boxheight * 0.5, boxheight * 0.5, 0.0, twistang);   
rotate(mat, tang, set(0, 1, 0));      

float scale = max(sin(fit(@P.y, -boxheight * 0.5, boxheight * 0.5, 0.0, $PI)), 0.01);    
scale(mat, set(scale, 1, scale));    

//添加代码
translate(mat, set(-bendrad, 0, 0));  //box沿-X轴移动
//box的高度进行映射，映射的角度范围为 (0.0,bendang)，当bendang = 2π时，即弯曲360°
float bang = fit(@P.y, -boxheight * 0.5, boxheight * 0.5, 0.0, bendang);    
rotate(mat, -bang, set(0, 0, 1));     //沿Z轴旋转

@P *= mat;

 结果为：基于上述条件，及弯曲半径bendrad = 2，弯曲角度bendang=1(即弯曲π)，

 ③扩展，对扭曲、弯曲的角度可添加帧相关代码，使其转起来

//看着位置添加，不懂就白学了
tang += $PI * 2 * @Frame / $FEND * chi('tangmult');     //引入帧相关，实现动态扭曲

bang += $PI / 2 * @Frame / $FEND;     //动态旋转/弯曲

结果为：基于上述条件，及扭曲速率tangmult = 3的情况下，(图片不够直观，可以看B站视频第十五节的2h48m17s)

18、小练3—逆变换

 eg.①继续使用【17、Exercise2——Twisting and Bending扭曲和弯曲】的案例，在代码节点最后一行添加代码，

//对变换后的矩阵进行存储，方便调用
4@mat = mat;

 ②在下方添加及连接类型为points的attributeWrangle节点并写入代码，

matrix mat = 4@mat;

matrix imat = invert(mat);

@P *= imat;

 结果为：box打回原形，

19、二面体函数

将方向从一个向量更改为另一个向量方向。

eg.①如下图所示创建节点：

②对节点进行设置：
line2、line3随便旋转下，color1、color2颜色随意；
polywire1节点是从线生成管道，细分设置8或者任意值；
dihedral节点类型为Points。
③在dihedral节点中写入以下代码，

vector cdir = normalize(point(1, 'P', 1));    //直线方向进行归一化
vector tdir = normalize(point(2, 'P', 1));    //直线方向进行归一化

matrix mat = dihedral(cdir, tdir);            //创建矩阵。不懂看官方文档

@P *= mat;

结果为：polywire对象由直线lin2(红色)的转向，变为直线line3(蓝色)的转向，

20、朝向函数

lookat() 函数用法官方文档截图如下，

该函数计算两个向量之间的差值向量（To-From），然后物体以-Z轴为起点旋转，旋转大小为两个向量的差值向量。
有点绕，点击可以看这个老哥的文章解释。

eg.理论：创建一个顶点指向-Z轴的圆锥，再创建一个随机点，使用 lookat() 函数使圆锥指向点。
实操：
①如下图创建节点，并进行一些必要设置：
circle1细分设置4；
transform1节点的Translate的Z轴改成-2；
polyloft1节点的U wrap选择On；
add1节点添加一个点，随便移动下；
lookat节点类型为Points，

 ②在lookat节点写入如下代码，

vector from = set(0, 0, 0);
vector to = point(1, 'P', 0);

float roll = chf('roll');                //范围0~360
matrix3 mat = lookat(from, to, roll);

@P *= mat;

 结果：圆锥指向随机点，滑动Roll值，变化如下图，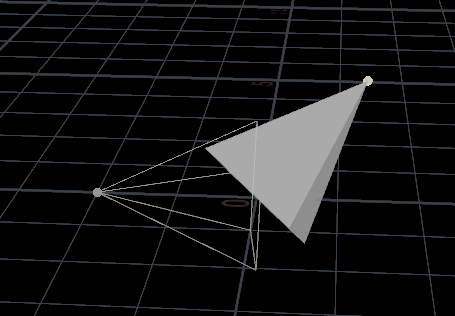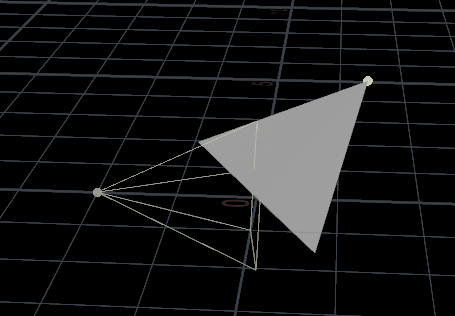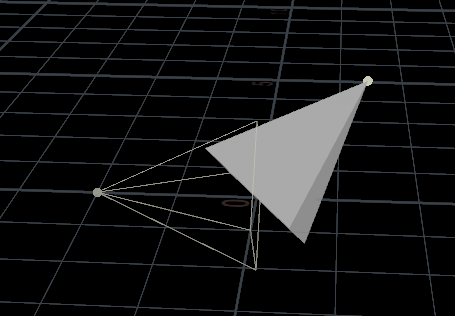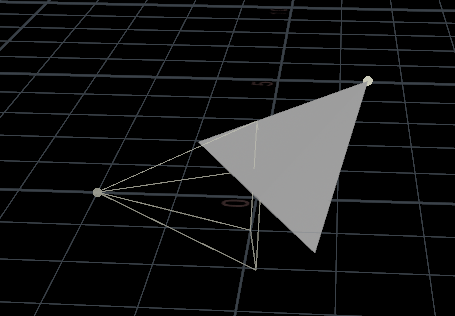

21、实例化函数

instance() 函数，创建一个给定参数的变换矩阵。类似复制。

eg.先上节点图及结果：

操作：可以拿【 20、Lookat VEX Function朝向函数】的案例进行修改，
①设置：
circle1细分设置4；
transform1节点的Translate的Z值改成2；
polyloft1节点的U wrap选择On；
sphere3节点类型为Polygon；
normal1节点的Add Normals to选择Points，即点法线；
foreach节点类型为for-Each Point；
instance节点类型为Points，
②instance节点写入代码，

vector pos = point(1, 'P', 0);              //点位置
vector norm = point(1, 'N', 0);               //点法线
vector scale= set(1, 1, abs(pos.y) + 0.25);     //缩放

matrix mat = instance(pos, norm, scale);

@P *= mat;

22、小练—矩阵插值

就是在两个矩阵变换中之间平滑过渡。

最好使用四元数进行旋转，而不是向量。

eg.直接使用【21、Instance VEX Function实例化函数】的案例，在instance节点添加代码，
完整代码如下：

vector pos = point(1, 'P', 0);              //点位置
vector norm = point(1, 'N', 0);               //点法线
vector scale= set(1, 1, abs(pos.y) + 0.25);     //缩放

matrix mat = instance(pos, norm, scale);        //矩阵mat为最终状态

vector t, r, s;
cracktransform(0, 0, set(0,0,0), mat, t, r, s);     //逆矩阵函数，把矩阵分解

float lerpval = chf('lerpval');                     //插值系数 / 平滑过渡系数

vector sl = lerp(set(1,1,1), s, lerpval);           //缩放插值，即缩放平滑过渡
vector tl = lerp(set(0,0,0), t, lerpval);           //位移插值，即位移旋转过渡
vector4 q = eulertoquaternion(radians(r), 0);       //旋转的欧拉角转为四元数，0表示旋转顺序
vector4 ql = slerp(quaternion(set(0,0,0)), q, lerpval);     //对旋转四元数进行插值
vector rl = quaterniontoeuler(ql, 0);                       //旋转插值，即旋转平滑过渡，0表示旋转顺序

matrix lmat = ident();
scale(lmat, sl);
rotate(lmat, rl, 0);
translate(lmat, tl);

@P *= lmat;

 结果：lerpval值0~1变化过程，