HoudiniVex笔记_P14_QuaternionBasics四元数基础

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5

1、Quaternion四元数

vector4 = (x, y, z, w)——表示物体的旋转角度(x、y、z)及旋转轴(w).

2、四元数声明

可在类型为detail的attributeWrangle节点验证查看以下代码值：

vector4 val = set(0, 1, 2, 3);

p@val = val;

float angle = radians(chf('ang'));      //旋转角度
vector axis = normalize(chv('axis'));   //旋转轴

vector4 val = quaternion(angle, axis);   //四元数：旋转角度、旋转轴

p@val = val;

3、四元数与旋转(可视化)

eg.① 添加一个Add节点(添加一个点)、一个attribcreate1节点(设置属性为方向向上的向量-->Name:N、Type:Vector、Value:1,0,0,0)、PointWrangle节点并写入以下代码：

float ang = radians(chf('ang'));
vector axis = normalize(chv('axis'));

v@axis = axis;

vector4 quat = quaternion(ang, axis);

@N = qrotate(quat, @N);    // qrotate()一个旋转函数，@N根据四元数进行旋转

② 对属性旋转轴@axis、旋转@N进行标记，以便观察。标记方法如下：

③设置旋转轴为 (0, 1, 0)，滑动旋转角度从0°~360°结果为：旋转轴@axis为黄色，旋转@N青色。
感兴趣可以尝试不同旋转轴的旋转变化.

4、练习1——旋转对象

给对象设置一个旋转轴。

eg.①设置节点Sphere小球(polygon)，convertiline节点(将小球转为线框，此步可有可无，仅方便观察，也可以直接在视图窗口进行设置)，PointWrangle节点(detail_object)、line直线节点(作旋转轴)、最后merge结合在一起。如下：

②下PointWrangle节点写入以下代码：

vector pos = point(1, 'P', 1);    //直线末点位置（起点(0, 0, 0)
vector axis = normalize(pos);     //将直线归一化，后面用作旋转轴

float ang = radians(chf('ang'));        //旋转角度
vector4 quat = quaternion(ang, axis);   //四元数，旋转轴+旋转角度

@P = qrotate(quat, @P);        //对象@P根据四元数，进行旋转

 结果为：直线为小球的旋转轴。滑动角度，小球以直线为中心旋转。

5、练习2——Sprial Rotation螺旋旋转

对线细分，进行螺旋旋转。

eg.创建一个直线line节点(类型polygon、Direction:1,0,0、Points:100)、一个PointWrangle节点，写入以下代码：

vector axis = set(0, 1, 0);                //旋转轴
float ang = @ptnum * radians(chf('ang'));    //旋转角度递增

vector4 quat = quaternion(ang, axis);

@P = qrotate(quat, @P);

 结果：滑动角度按钮，下图为角度0~180之间的变化(半径——>直径)，

6、欧拉角转四元数

在3D空间中，还可以使用Euler欧拉角表示物体旋转，欧拉角包括3个旋转，根据这3个旋转来指定一个刚体的朝向，这3个旋转分别绕x轴，y轴和z轴，

eulertoquaternion()函数，参数order表示旋转轴方向，可使用int也开始使用下面代码内的用法。
更具体的用法可以查看官方文档介绍，或者直接查看Houdini自带的外部函数(安装路径\houdini\vex\include)math.h脚本查看用法。
其实就是咱日常使用的旋转，不同旋转顺序，结果又不同，大概如下：

eg.① 添加一个Add节点(添加一个点)、一个attribcreate1节点(设置属性为方向向上的向量-->Name:N、Type:Vector、Value:1,0,0,0)、PointWrangle节点并写入以下代码：

vector angles = chv('angles');
angles = radians(angles);

//可尝试比较不同旋转顺序的不同结果 XFORM_XZY、XFORM_YZX、……
vector4 quat = eulertoquaternion(angles, XFORM_XYZ);

p@quat = quat;

@N = qrotate(quat, @N);

 结果为：对@N、@quat进行标记，旋转顺序为XFORM_XYZ时，改变旋转角度angles的X值，实际上物体/点没有旋转或者任何变化，因为要旋转的轴已经在X轴上了。
感兴趣可以再添加个box之类代替点去验证下。

7、四元数转欧拉角

eg.在【6、Euler to Quaternion欧拉角转四元数】下面添加一个PointWrangle节点，

vector4 quat = p@quat;

vector euler = quaterniontoeuler(quat, XFORM_XYZ);

v@euler = degrees(euler);

结果：euler值与【6、Euler to Quaternion欧拉角转四元数】的angles值相同。

8、四元数旋转与插值过渡

在两个四元数值之间创建平滑过渡。
下面例子可以看到不同平滑参数(0~1)值的过渡变化。

eg.先上节点连接图：

操作：
①创建一个add节点(添加一个点)，
②PointWrangle1节点，并写入以下代码：

//旋转对象1
@N = set(0, 1, 0);                  //设置一个向量

float ang = radians(chf('ang'));    //范围设置为0~360
vector axis = set(1, 0, 0);         //设置旋转轴

vector4 quat = quaternion(ang, axis);   //四元数：旋转角度、旋转轴
@N = qrotate(quat, @N);                 //@N根据四元数旋转

int pt = addpoint(0, @N);
int line = addprim(0, 'polyline', @ptnum, pt);  //Add点(0,0,0)与@N点创建条线

setdetailattrib(0, 'quat1', quat);           //对直线创建个detail属性

③继续添加一个并排节点PointWrangle2节点，写入以下代码：

//旋转对象2
@N = set(0, 1, 0);                  //设置一个向量

float ang = radians(chf('ang'));    //范围设置为0~360
vector axis = set(0, 0, 1);         //设置旋转轴

vector4 quat = quaternion(ang, axis);   //四元数：旋转角度、旋转轴
@N = qrotate(quat, @N);                 //@N根据四元数旋转

int pt = addpoint(0, @N);
int line = addprim(0, 'polyline', @ptnum, pt);  //Add点(0,0,0)与@N点创建条线

setdetailattrib(0, 'quat2', quat);           //对直线创建个detail属性

③添加merge节点，连接上面两个Pointw节点/旋转对象，再添加一个DetailWrangle节点，写入以下代码：

vector4 quat1 = p@quat1;
vector4 quat2 = p@quat2;

vector norm = set(0, 1, 0);
vector4 quat3 = slerp(quat1, quat2, chf('t'));
norm = qrotate(quat3, norm);

//搞条线，方便观察混合旋转的样子
int pt1 = addpoint(0, set(0, 0, 0));
int pt2 = addpoint(0, norm);
int line = addprim(0, 'polyline', pt1, pt2);

结果：对两旋转对象设置随便角度值（青色线），其混合变化为（白色线），
因混合值也包含旋转轴，所以它的混合插值变化稍显弧度状，

9、练习3——Rotation Animation旋转动画

一个矩形，随机旋转一个角度，再随机旋转一个角度，再随机旋转……

eg.使用循环函数 foreach() 与随机函数 rand() 生成随机旋转角度，再用混合函数slerp()将旋转平滑过渡。
节点连接图如下：

操作：一些代码及设置
①to_detail_attrib节点(detail类型)写入以下代码：

vector roteuler = radians(chv('roteuler'));             //获取Transform节点的随机旋转值，每次循环旋转都不一样

vector4 quat = eulertoquaternion(roteuler, XFORM_XYZ);  //欧拉角转四元数：旋转角度，旋转顺序
int ite = detail(1, 'iteration');                       //ite=detail属性的循环值，1,2,3,4,5，……

setdetailattrib(0, 'quat' + itoa(ite), quat);     //对quat设置detail属性，
                                                  //itoa()函数把整数转为字符串，quat1、quat2、quat3、……

 ②rotation_slerp(point类型)节点写入以下代码

int num = chi('num');                   //已与循环次数复制引用，该值表示循环次数

float range = $FEND / float(num);       //总帧数除以循环次数，得到每次旋转过渡的时间范围
float t = (@Frame % range) / range;     //在时间范围range内，当前循环时间在范围内的占比(最大值为1)，
                                        //比如循环次数为6，当前帧为240帧，则每次旋转时间范围为40帧，在第70帧时，t=30/40
int curnum = floor(@Frame / range) % num;   //当前循环次数，floor()函数返回小于或等于参数的最大整数
int nexnum = (curnum + 1) % num;           //下一次循环次数，取余数运算，算是给运算加一层保险

vector4 curquat = detail(1, 'quat' + itoa(curnum));     //itoa()函数把int整数转为字符串
vector4 nexquat = detail(1, 'quat' + itoa(nexnum));     //下一次旋转角度

vector4 quat = slerp(curquat, nexquat, t);              //旋转过渡

@P = qrotate(quat, @P);

 ③Transform节点设置：
每个Rotate值写入：其中，detail('../foreach_count1/', 'iteration', 0)指当前迭代次数，
rand(detail('../foreach_count1/', 'iteration', 0) + 3.215) * 360、
rand(detail('../foreach_count1/', 'iteration', 0) + 5.618) * 360、
rand(detail('../foreach_count1/', 'iteration', 0) + 15.85) * 360。
最后结果大概如下：(非固定值，随机就行，但范围最后是0~360之间)

④to_detail_attrib节点(detail类型)设置如下：
在to_detail_attrib节点的roteluer通道粘贴相对引用<——复制Transform节点的rotate值；
⑤rotation_slerp(detail类型)节点设置如下：
在rotation_slerp节点的num通道复制值——>在foreach_end1节点的interations值出粘贴相对引用；

 结果为：设置循环次数为6，box尺寸为(0.2, 0.5, 1)，初始角度随意，下图仅显示为0帧到80帧的旋转结果，

10、二面体与定向向量

dihedral ()函数：计算一个向量定到另一个向量的四元数，即一个向量到另一个向量的旋转角度、旋转轴。
如下图所示，line3旋转到line4，我们把圈圈定向到【line3旋转到line4】，又或者说圈圈替换为旋转后的line4。【4、练习1——Rotate Object旋转对象】仅是设置旋转轴，本次为定向到旋转后的状态，

eg.先上结果：

 操作：
line4随便旋转下，PointWrangle节点写入以下代码：

vector dir1 = normalize(point(1, 'P', 1));
vector dir2 = normalize(point(2, 'P', 1));

vector4 quat = dihedral(dir1, dir2);    //计算一个向量到另一个向量的四元数
@P = qrotate(quat, @P);                 //圈圈根据四元数旋转

11、练习4——二面体动画

object对象在小球表面转圈圈。
理论：A)利用三角函数让点动起来，运动路径的形状如小球形状；B)获取点位置的小球法线；C)
Y轴向与法线组成二面体，Object定向到二面体。

先上结果：下图结果仅部分，圈数为2，帧数0~90帧(总帧数240帧)，

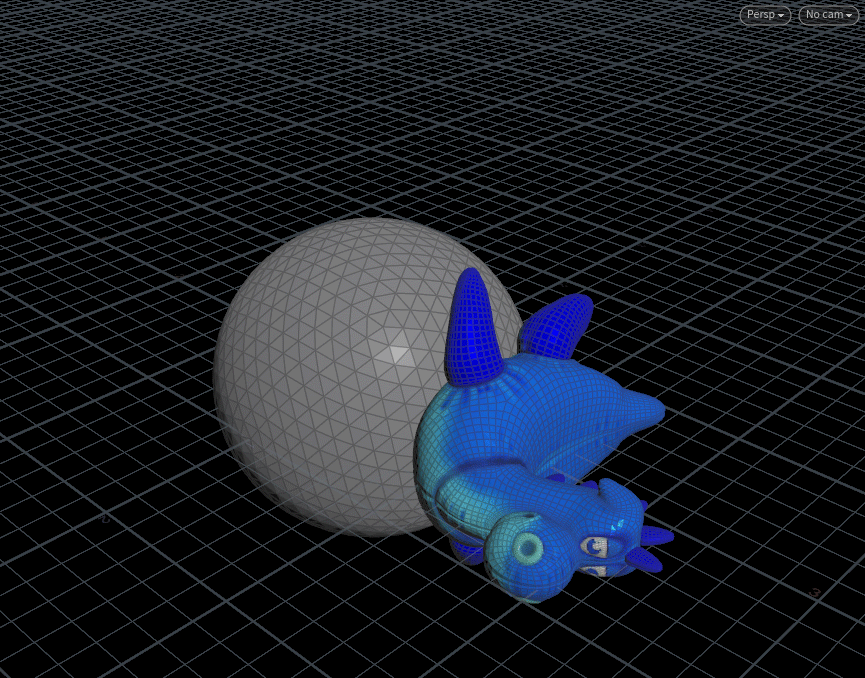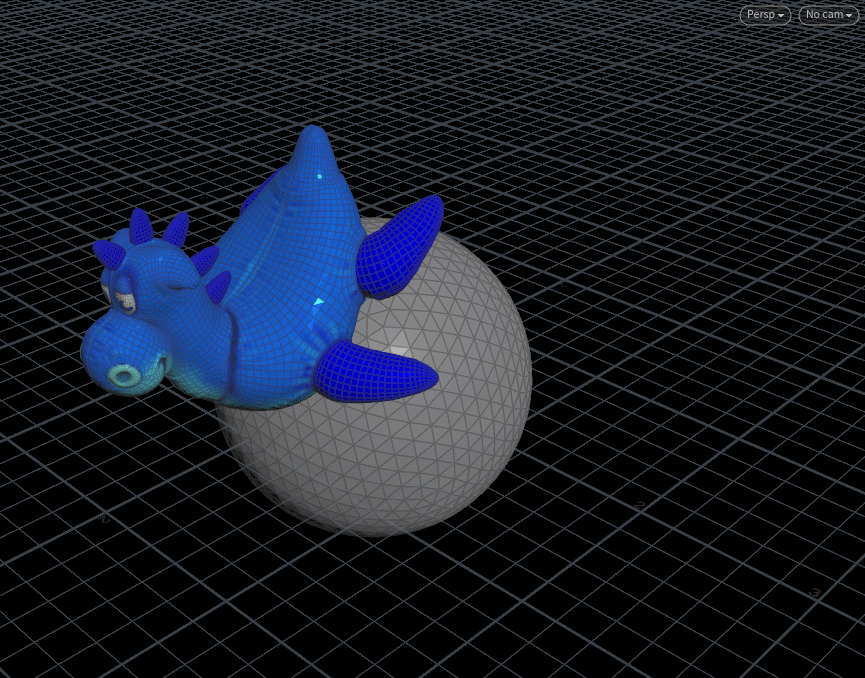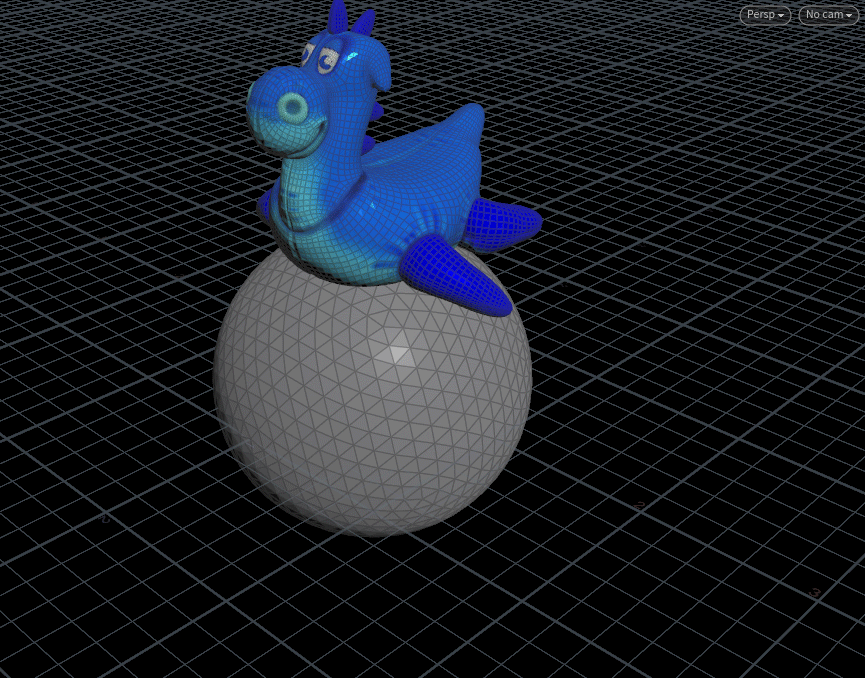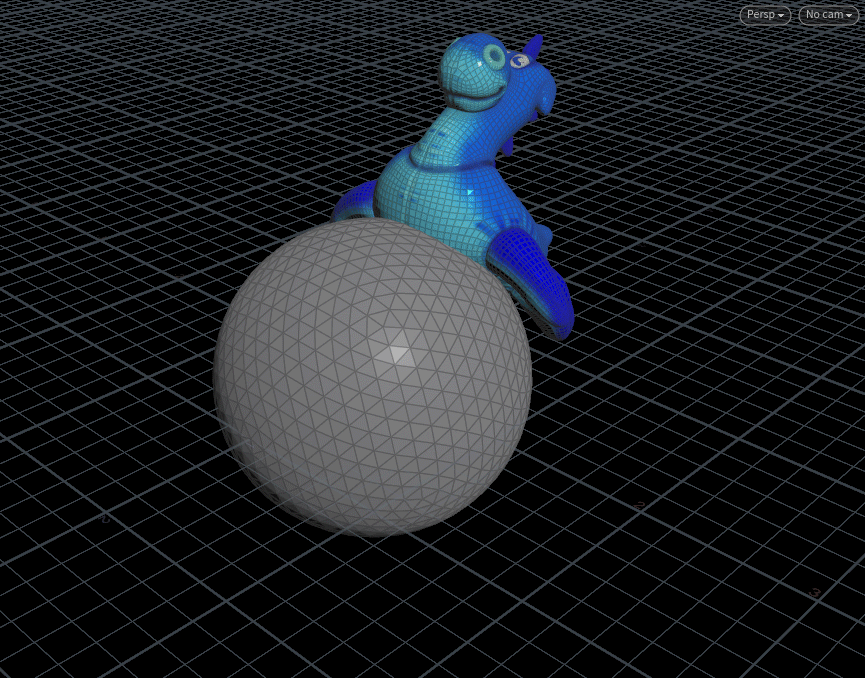
 eg.节点连接及设置：

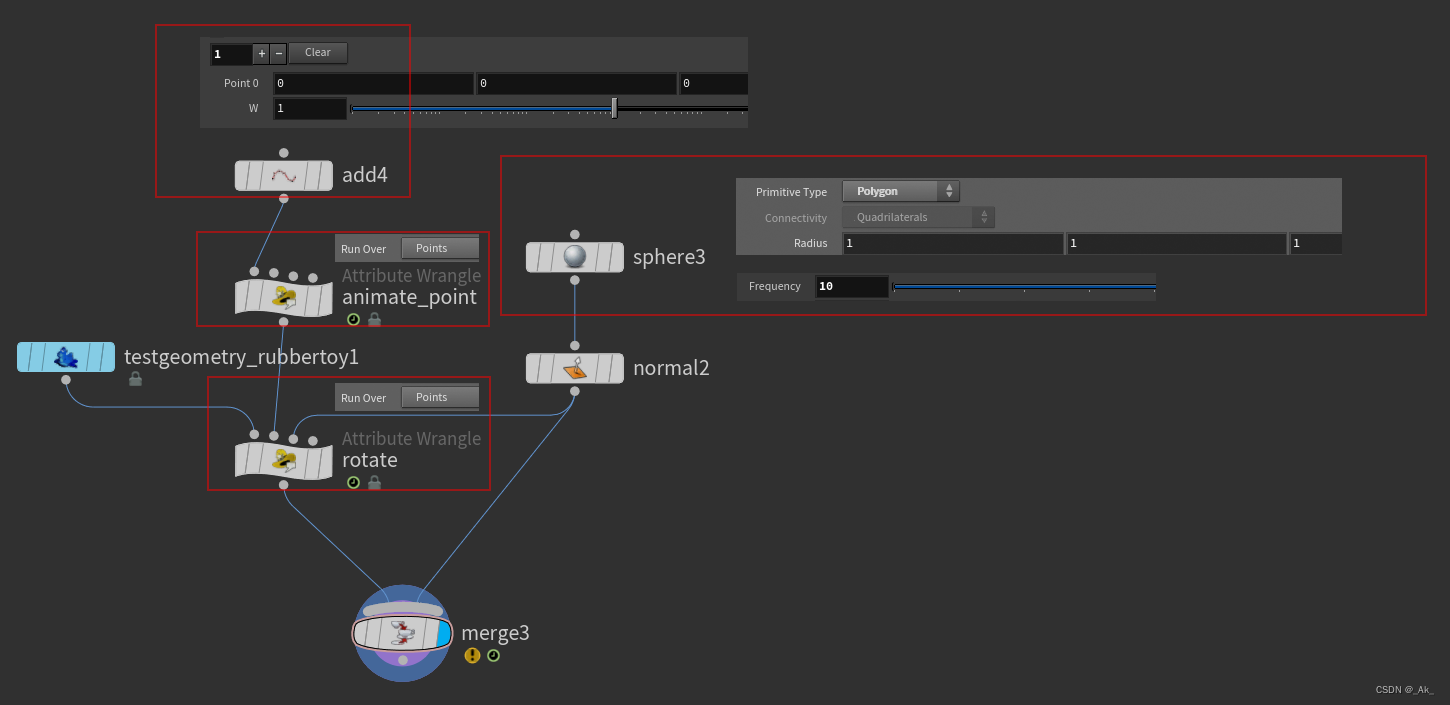
 其中，animate_point节点写入以下代码：

//点绕小球转圈圈（点运动形状如小球）
float ang = $PI * 2.0 * @Frame / $FEND;     //时间开始到结束，角度0~360°
float h = sin(ang);                         //半径为1，sinθ值作为高度（Y坐标）
float rad = sqrt(1.0 - pow(h, 2.0));        //勾股定理，在某一帧时，点在X、Z方向的长度

float ang2 = $PI * 2.0 * @Frame / $FEND * chi('num');       //自定义旋转圈数
vector pos = set(cos(ang2) * rad, h, sin(ang2) * rad);

@P = pos;   //点更新位置

rotate节点写入以下代码：

vector pos = point(1, 'P', 0);              //点的位置
vector norm = uvsample(2, 'N', 'P', pos);   //点位置的小球法线。uvsample()函数，给定坐标信息，返回指定属性值

vector4 quat = dihedral(set(0, 1, 0), norm);    //Y轴向量与法线——》二面体
@P = qrotate(quat, @P);                         //定向到二面体

@P += pos;                  //更改Object中心点