分类问题的概率校准

一 背景：

对于某个不确定问题，每个人都会给出一个判断即主观概率，事物实际发生的概率是客观概率，概率校准是衡量主观概率与客观概率之间一致程度的方法，如果一个人的主观概率判断经常比客观概率大，则过份自信，相反就是过低自信。朴素贝叶斯是过分自信的分类器，支持向量机是过低自信的分类器，逻辑回归往往能给出较好的概率预测。

分类器分类的结果即score,而非probability，是由于分类器给出的概率结果与真实的概率分布差别较大。

分类模型得到类别概率结果有2条解决路径：

1 直接建立概率分类模型，如使用logistic回归、朴素贝叶斯、随机森林等输出预测的概率结果，从而依据结果判定类别，如结果大于0.5则为正样本等；

2 通过对分类结果进行再学习得到概率，即概率校准。

二 概率校准的作用：

 1 将非概率分类模型的输出转化为概率；

2 对概率分类模型的结果进行进一步修正。

三 实现概率校准的方法：

1 参数方法：Platt Scaling(sigmoid),将分类模型的输出结果通过Sigmoid函数转化为概率，即校准后的概率

Isotonic回归：找到一个能够拟合数据点的单调递增函数，同时最小化均方误差，即一分类器输出的每个样本的概率值作为自变量，以样本的真实值作为因变量，来拟合单调递增函数；在测试时，先根据分类器给出原始概率，然后使用拟合出来的函数计算校准后的概率

2 非参数方法：Histogram Binning,对所有未知样本x根据分类模型原始输出得分进行排序，然后将其分成若干等频箱体，再计算每个箱体内正样本数目

四 对模型校准结果的评价：

1 Brier Score评分：概率估计值和实际样本类别值之间的均方误差，pi是预测概率，yi是实际类别，N是样本数量，Brier Score越低，代表校准结果越好。

2 Reliability Diagram可靠性图：可视化的评价方法，将预测概率分为N个区间[0,1/N],[1/N,2/N]以此类推，可靠性图通过绘制预测概率与实际类别频率之间关系的校准曲线来展示和评价校准结果。

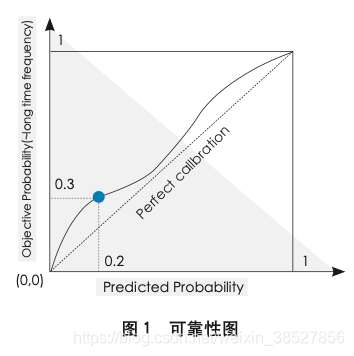
如图 1 所示校准曲线上的 每一个点的横坐标表示落入某预测区 间的样本概率平均预测值，纵坐标表 明了该区间内正类样本数目的关系。 校准曲线越接近对角线虚线，代表校 准结果越好完美的。图 1 所示的校准 曲线中，黄色圆点表明当样本预测概 率约为 0.2 时，约有 30% 的样本比例 属于正类，概率预测值略有偏低。

在训练集进行概率校正，利用测试集检验模型预测和校正的效果

五 随机森林的概率校准

前提：分类树的森林比概率估计树(PET)的森林的均方误差要低，分类效果好，原因是：概率估计树的森林的结果的概率分布是通过平均每个PET的概率分布得来的；而分类树的森林，在形成平均分布前每个个体的概率分布被一个极端版本所取代，将最可能的类别设为1，其他类别设为0。这个结果导致了分类准确率的提高

新的概率校准方法：纠正每个独立的概率分布去替代是纠正结果里的平均概率分布，表示随机森林里是分类树而不是概率估计树；仅为最有可能的类别增加估计概率

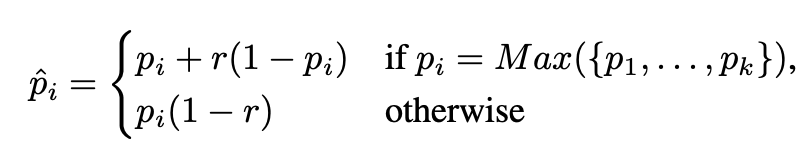
如何获得校准设置：训练集的每个例子，都有一对带有独立训练分类器得分的校准设置