手把手教你 DVOL

分享本文在朋友圈的读者可获得本文数据和 Python 代码。留个言说已分享（不用截屏）我相信你，我会发给你百度盘下载链接。

本文长度为 6393 字，建议阅读 32 分钟

题图：SignalPlus Dashboard

0

引言

---

Deribit volatility (DVOL) 指数是 Deribit 制定的加密货币期权的波动率指数，它衡量的是 30 天的向前看 (forward-looking) 预期波动率 (implied volatility 从期权价格隐含计算出来)，而不是向后看 (backward-looking) 实际波动率 (realized volatility 从标的价格时间序列计算)。

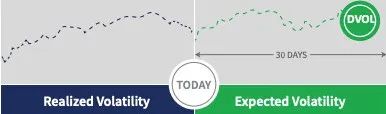
DVOL 是一个年化波动率的预期。粗略来讲，要获得 BTC 价格每日的预期变动，只需将 DVOL 值除以 19 (365 的平方根) 即可。 例如，DVOL 等于 57 (其实指的是 57%) 相当于 3% 的日波动。

和老规矩一样，在前戏王中我会介绍推导所需要的知识点；在理论皇中我会根据不同市场惯例给出不同的波动率指数表达式，如股票市场的 VIX 和币圈市场的 DVOL；在实践狼中我会讲解如何用 Python 来计算 DVOL。

LET'S GO!

1

前戏王

---

1.1

方差期望

假设标的资产的 SDE 和经过伊藤定理变形后的 SDE 如下：

第 2 个公式减去第 1 个公式后，两边乘以 2 得到：

两边从 0 到 T 求积分得到：

两边求期望得到：

上式中的 F_0,T 是标的资产在 T 时到期的远期价格，而左边的期望值年化后 (除以 T) 就是方差，即

1.2

Carr & Madan 公式

Carr & Madan 公式是本文证明需要的核心内容，公式如下：

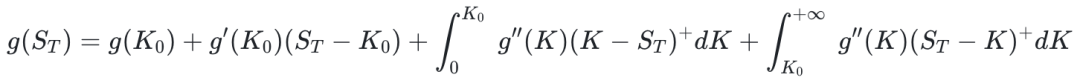
该公式咋一看很复杂，实际上就是利用了泰勒展开。在实操时，可把 g(S_T) 看成某个金融产品的支付函数，右边积分项里有 put 和 call 的支付函数，这样对于任何一个金融产品，其支付函数都可以用一系列的 put 和 call 来合成。 

为了推导波动率指数，我们选取对数合约作为这个金融产品。

推导见 https://gregorygundersen.com/blog/2023/01/26/carr-madan/。

1.3

对数合约

对数合约 (log contract) 是一种奇异期权 (exotic option)，它根据其标的资产价格的对数进行支付。对数合约的收益是单一资产价格的非线性函数。这种类型的期权使投资者表达对未来波动的看法。

给定对数合约的支付函数 g(x) = ln(x/S*)，其一阶导数和二阶导数为

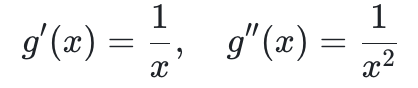
注意到小节 1.1 最后得到公式里红色那一项就是对数合约的期望，利用对数性质 ln(ab) = ln(a) + ln(b) 做以下的恒等变换：

代入 Carr & Madan 公式得到

两边求期望可计算出