2.一起学习机器学习 -- Linear_regression

Prerequisites

• Basic familiarity with Numpy
• Basic familiarity with Pyplot

Outline

• Section 0: NumPy Tips and Code Clarity
• Section 1: Intro to Linear Regression
• Section 2: Least Squared Loss and Maximum Likelihood
• Section 3: Ridge Regression
• Section 4: LASSO Regression

Section 0: NumPy Tips and Code Clarity

There are multiple ways in NumPy to do each of the following basic operations:

• Matrix-matrix and matrix-vector product.
• Matrix-matrix and vector-vector element-wise product.
• vector-vector inner and outer products.

Avoid using general functions such as np.dot that handles most of these operations depending on the shapes of the input parameters.

Note: to check a function documentation, you can do that inside a Nootbook cell using ?<function_name>.

import numpy as np
?np.dot

[0;31mCall signature:[0m  [0mnp[0m[0;34m.[0m[0mdot[0m[0;34m([0m[0;34m*[0m[0margs[0m[0;34m,[0m [0;34m**[0m[0mkwargs[0m[0;34m)[0m[0;34m[0m[0;34m[0m[0m
[0;31mType:[0m            _ArrayFunctionDispatcher
[0;31mString form:[0m     <built-in function dot>
[0;31mDocstring:[0m      
dot(a, b, out=None)

Dot product of two arrays. Specifically,

- If both `a` and `b` are 1-D arrays, it is inner product of vectors
  (without complex conjugation).

- If both `a` and `b` are 2-D arrays, it is matrix multiplication,
  but using :func:`matmul` or ``a @ b`` is preferred.

- If either `a` or `b` is 0-D (scalar), it is equivalent to
  :func:`multiply` and using ``numpy.multiply(a, b)`` or ``a * b`` is
  preferred.

- If `a` is an N-D array and `b` is a 1-D array, it is a sum product over
  the last axis of `a` and `b`.

- If `a` is an N-D array and `b` is an M-D array (where ``M>=2``), it is a
  sum product over the last axis of `a` and the second-to-last axis of
  `b`::

    dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

It uses an optimized BLAS library when possible (see `numpy.linalg`).

Parameters
----------
a : array_like
    First argument.
b : array_like
    Second argument.
out : ndarray, optional
    Output argument. This must have the exact kind that would be returned
    if it was not used. In particular, it must have the right type, must be
    C-contiguous, and its dtype must be the dtype that would be returned
    for `dot(a,b)`. This is a performance feature. Therefore, if these
    conditions are not met, an exception is raised, instead of attempting
    to be flexible.

Returns
-------
output : ndarray
    Returns the dot product of `a` and `b`.  If `a` and `b` are both
    scalars or both 1-D arrays then a scalar is returned; otherwise
    an array is returned.
    If `out` is given, then it is returned.

Raises
------
ValueError
    If the last dimension of `a` is not the same size as
    the second-to-last dimension of `b`.

See Also
--------
vdot : Complex-conjugating dot product.
tensordot : Sum products over arbitrary axes.
einsum : Einstein summation convention.
matmul : '@' operator as method with out parameter.
linalg.multi_dot : Chained dot product.

Examples
--------
>>> np.dot(3, 4)
12

Neither argument is complex-conjugated:

>>> np.dot([2j, 3j], [2j, 3j])
(-13+0j)

For 2-D arrays it is the matrix product:

>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
       [2, 2]])

>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128
[0;31mClass docstring:[0m
Class to wrap functions with checks for __array_function__ overrides.

All arguments are required, and can only be passed by position.

Parameters
----------
dispatcher : function or None
    The dispatcher function that returns a single sequence-like object
    of all arguments relevant.  It must have the same signature (except
    the default values) as the actual implementation.
    If ``None``, this is a ``like=`` dispatcher and the
    ``_ArrayFunctionDispatcher`` must be called with ``like`` as the
    first (additional and positional) argument.
implementation : function
    Function that implements the operation on NumPy arrays without
    overrides.  Arguments passed calling the ``_ArrayFunctionDispatcher``
    will be forwarded to this (and the ``dispatcher``) as if using
    ``*args, **kwargs``.

Attributes
----------
_implementation : function
    The original implementation passed in.

# shape: (2, 2)
A = np.array([[1, 2], [3, 4]])

# shape: (2, 2)
B = np.array([[5, 6], [7, 8]])

# shape: (2, )
v1 =  np.array([5, 6])

# shape: (3, )
v2 = np.array([4, 5, 6])

# shape: (2, )
v3 = np.arange(8, 11)

result_matrix_matrix = np.dot(A, B)
# result_matrix_matrix = A @ B # Better


result_matrix_matrix

array([[19, 22],
       [43, 50]])

result_matrix_vector = np.dot(A, v1)
# result_matrix_vector = A @ v1 # Better
result_matrix_vector

array([17, 39])

result_inner_product = np.dot(v2, v3)
# result_inner_product = np.inner(v2, v3)
result_inner_product

137

There are several issues in using np.dot in the previous cells. It can be very confusing to read a code with np.dot as you are trying to understand what operation is actually intended. The reader is required first to read the documentation of np.dot and then probe the shape of the input parameters to interpret the expression.

To avoid confusion, consider the following practice:

• Use the explicit @ operator for matrix-matrix and matrix-vector products.
• Use the explicit * operator for element-wise products or broadcasted products.
• Use the explicit np.inner function for innter product between 1-D vectors, same for np.outer function.

When you intend to work with an object as a 1-D vector, make sure you don’t have excessive dimensions with size 1 of your array.

# shape: (1, 2)
v4 = np.array([[5, 6]])

# shape: (2, 1)
v5 = np.array([[5], [6]])

# This works due to broadcasting rules.
v4 * v5

array([[25, 30],
       [30, 36]])

f'v4.shape: {v4.shape}, v5.shape: {v5.shape},  v4.ndim: {v4.ndim},  v5.ndim: {v5.ndim}'

'v4.shape: (1, 2), v5.shape: (2, 1),  v4.ndim: 2,  v5.ndim: 2'

To fix this and deal with them as vectors:

v4 = v4.squeeze() # Now shape: (2, )
v5 = v5.squeeze() # Now shape: (2, )

f'v4.shape: {v4.shape}, v5.shape: {v5.shape},  v4.ndim: {v4.ndim},  v5.ndim: {v5.ndim}'

'v4.shape: (2,), v5.shape: (2,),  v4.ndim: 1,  v5.ndim: 1'

v4 * v5

array([25, 36])

General practice to improve readability and avoid unexpected behaviour:

• When possible use explicit expressions instead of general functions like np.dot.
• Ensure objects representing 1-D vectors have ndim==1. If you are writing a function that deals with vectors and parameters use assert statements to make sure the input parameters match what you expect.
• Never use the deprectated np.matrix class but always np.array.

Linear Regression

Section 1: Intro to Linear regression

Partly adapted from Deisenroth, Faisal, Ong (2020).

The purpose of this notebook is to practice implementing some linear algebra (equations provided) and to explore some properties of linear regression.

We will mostly rely on the Python packages numpy and matplotlib, and you are not allowed to use any package that has a complete linear regression framework implemented (e.g., scikit-learn).

import numpy as np
import matplotlib.pyplot as plt

# Initial global configuration for matplotlib
SMALL_SIZE = 12
MEDIUM_SIZE = 16
BIGGER_SIZE = 20

plt.rc('font', size=SMALL_SIZE)          # controls default text sizes
plt.rc('axes', titlesize=SMALL_SIZE)     # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE)    # fontsize of the x and y labels
plt.rc('xtick', labelsize=SMALL_SIZE)    # fontsize of the tick labels
plt.rc('ytick', labelsize=SMALL_SIZE)    # fontsize of the tick labels
plt.rc('legend', fontsize=SMALL_SIZE)    # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE)  # fontsize of the figure title

We consider a linear regression problem of the form
$$y={\mathbf{x}}^T\mathbf{\beta }+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2)$$
where $\mathbf{x}\in {\mathbb{R}}^{(p+1)}$ are inputs and $y\in \mathbb{R}$ are noisy observations. The parameter vector $\mathbf{\beta }\in {\mathbb{R}}^{(p+1)}$ parametrizes the function.

We assume we have a training set $({\mathbf{x}}_n,y_n)$, $n=1,\dots ,N$. We summarize the sets of training inputs in $\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N{]}^T$ and corresponding training targets $\mathbf{y}=[y_1,\dots ,y_N{]}^T$, respectively.

In this tutorial, we are interested in finding parameters $\mathbf{\beta }$ that map the inputs well to the ouputs.

From our lectures, we know that the parameters $\mathbf{\beta }$ found by the following equation are optimal:
$$\underset{\mathbf{\beta }}{\min }\Vert \mathbf{y}-\mathbf{X}\mathbf{\beta }{\Vert }^2=\underset{\mathbf{\beta }}{\min }{\text{L}}_{\text{LS}}(\mathbf{\beta })$$
where ${\text{L}}_{\text{LS}}$ is the (ordinary) least squares loss function.

Dataset generation

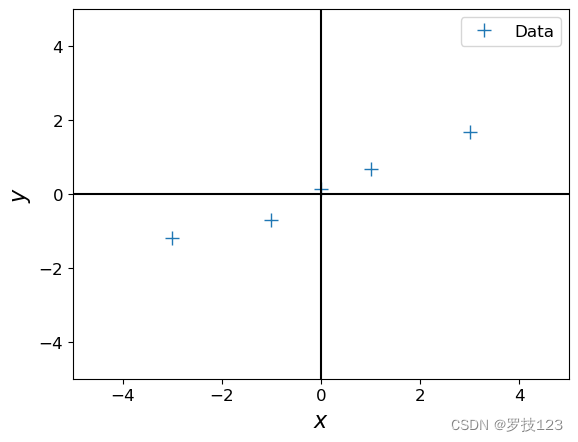
We will start with a simple training set, that we define by ourselves.

# Define training set
X = np.array([-3, -1, 0, 1, 3]).reshape(-1,1) # 5x1 vector, N=5, D=1
y = np.array([-1.2, -0.7, 0.14, 0.67, 1.67]).reshape(-1,1) # 5x1 vector

# Plot the training set

plt.figure()
plt.plot(X, y, '+', markersize=10, label='Data')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.ylim(-5, 5)
plt.xlim(-5,5)
plt.legend()

<matplotlib.legend.Legend at 0x1341c3bd0>

​

​

Section 2: Least squares loss and Maximum likelihood

From our lectures, we know that the parameters $\mathbf{\beta }$ found by optimizing following equation:
$$\underset{\mathbf{\beta }}{\min }\Vert \mathbf{y}-\mathbf{X}\mathbf{\beta }{\Vert }^2=\underset{\mathbf{\beta }}{\min }{\text{L}}_{\text{LS}}(\mathbf{\beta })$$
where ${\text{L}}_{\text{LS}}$ is the (ordinary) least squares loss function. The solution is
$${\mathbf{\beta }}^{\ast }=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}\in {\mathbb{R}}^{(p+1)},$$
where
$$\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N{]}^T\in {\mathbb{R}}^{N\times (p+1)},\mathbf{y}=[y_1,\dots ,y_N{]}^T\in {\mathbb{R}}^N.$$

The same estimate of $\mathbf{\beta }$ we can be obtained by maximum liklihood estimation which gives statistical interpretation of linear regression. In maximum likelihood estimation, we can find the parameters ${\mathbf{\beta }}^{\mathrm{ML}}$ that maximize the likelihood
$$p(\mathbf{y}|\mathbf{X},\mathbf{\beta })=\prod _{n=1}^{N}p(y_n|{\mathbf{x}}_n,\mathbf{\beta }).$$
From the lecture we know that the maximum likelihood estimator is given by
$${\mathbf{\beta }}^{\text{ML}}=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}.$$

Let us compute the maximum likelihood estimate for the given training set.

## EDIT THIS FUNCTION
def max_lik_estimate(X, y):

    # X: N x D matrix of training inputs
    # y: N x 1 vector of training targets/observations
    # returns: maximum likelihood parameters (D x 1)

    N, D = X.shape
    beta_ml = np.linalg.solve(X.T @ X, X.T @ y) ## <-- SOLUTION
    return beta_ml

print(X.T @ X)

[[20]]

print(np.dot(X.T, X))

[[20]]

#np.linalg.solve(a, b) -> gives a^(-1)b

# get maximum likelihood estimate
beta_ml = max_lik_estimate(X,y)

Now, make a prediction using the maximum likelihood estimate that we just found.

## EDIT THIS FUNCTION
def predict_with_estimate(X_test, beta):

    # X_test: K x D matrix of test inputs
    # beta: D x 1 vector of parameters
    # returns: prediction of f(X_test); K x 1 vector

    prediction = X_test @ beta ## <-- SOLUTION

    return prediction

beta_ml

array([[0.499]])

Let’s see whether we got something useful:

# define a test set
X_test = np.linspace(-5,5,100).reshape(-1,1) # 100 x 1 vector of test inputs
#beta_ml = np.array([[0.2]]) -> changes slope
# predict the function values at the test points using the maximum likelihood estimator
ml_prediction = predict_with_estimate(X_test, beta_ml)

# plot
plt.figure()
plt.plot(X, y, '+', markersize=10, label='Data')
plt.plot(X_test, ml_prediction, label='Linear Regression Fit')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.ylim(-5, 5)
plt.xlim(-5,5)
plt.legend()

<matplotlib.legend.Legend at 0x134801050>

​

​

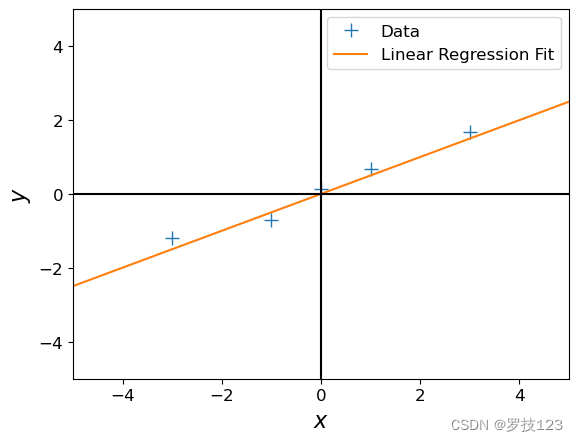
Questions

1. Does the solution above look reasonable?
2. Play around with different values of $\beta$. How do the corresponding functions change?
3. Modify the training targets $\mathcal{Y}$ and re-run your computation. What changes?

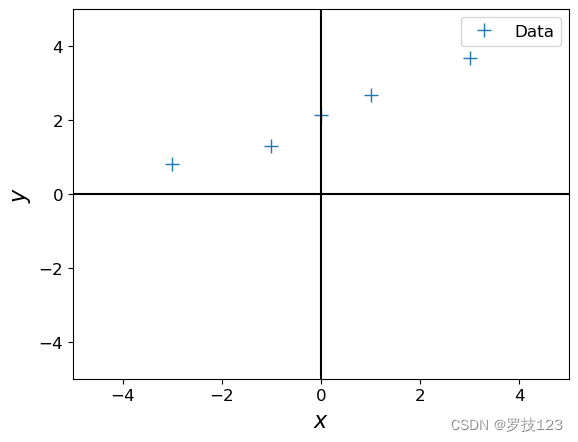
Let us now look at a different training set, where we add 2.0 to every $y$-value, and compute the maximum likelihood estimate.

ynew = y + 2.0

plt.figure()
plt.plot(X, ynew, '+', markersize=10, label='Data')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.ylim(-5, 5)
plt.xlim(-5,5)
plt.legend()

<matplotlib.legend.Legend at 0x1348b8710>

​

# get maximum likelihood estimate
beta_ml = max_lik_estimate(X, ynew)
print(beta_ml)

# define a test set
X_test = np.linspace(-5,5,100).reshape(-1,1) # 100 x 1 vector of test inputs

# predict the function values at the test points using the maximum likelihood estimator
ml_prediction = predict_with_estimate(X_test, beta_ml)

# plot
plt.figure()
plt.plot(X, ynew, '+', markersize=10, label='Data')
plt.plot(X_test, ml_prediction, label='Linear Regression Fit')
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.ylim(-5, 5)
plt.xlim(-5,5)
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()

[[0.499]]





<matplotlib.legend.Legend at 0x1347a00d0>

​

​

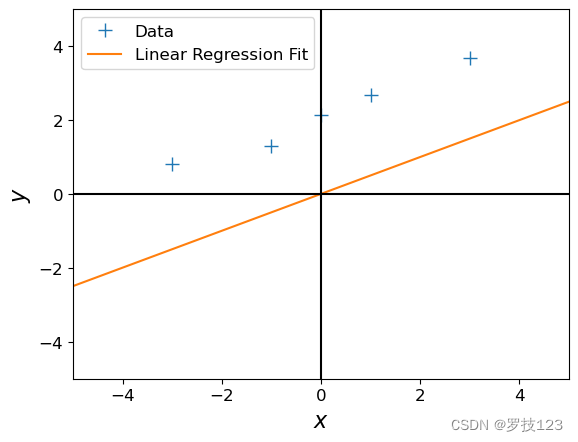
Question:

1. This maximum likelihood estimate doesn’t look too good: The orange line is too far away from the observations although we just shifted them by 2. Why is this the case?
2. How can we fix this problem?

Let us now define a linear regression model that is slightly more flexible:
$$y={\beta }_0+{\mathbf{x}}^T{\mathbf{\beta }}_1+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2)$$

Here, we added an offset (also called bias or intercept) parameter ${\beta }_0$ to our original model.

Question:

1. What is the effect of this bias parameter, i.e., what additional flexibility does it offer?

If we now define the inputs to be the augmented vector ${\mathbf{x}}_{\text{aug}}=\left[\begin{array}{c}1\\ \mathbf{x}\end{array}\right]$, we can write the new linear regression model as
$$y={\mathbf{x}}_{\text{aug}}^T{\mathbf{\beta }}_{\text{aug}}+ϵ,{\mathbf{\beta }}_{\text{aug}}=\left[\begin{array}{c}{\beta }_0\\ {\mathbf{\beta }}_1\end{array}\right].$$

N, D = X.shape
X_aug = np.hstack([np.ones((N,1)), X]) # augmented training inputs of size N x (D+1)
beta_aug = np.zeros((D+1, 1)) # new beta vector of size (D+1) x 1

Let us now compute the maximum likelihood estimator for this setting.

Hint: If possible, re-use code that you have already written.

## EDIT THIS FUNCTION
def max_lik_estimate_aug(X_aug, y):

    beta_aug_ml = max_lik_estimate(X_aug, y) ## <-- SOLUTION: simply have the same formula where you use the augmented predictor vector

    return beta_aug_ml

beta_aug_ml = max_lik_estimate_aug(X_aug, ynew)

beta_aug_ml # offset + slope

array([[2.116],
       [0.499]])

Now, we can make predictions again:

# define a test set (we also need to augment the test inputs with ones)
X_test_aug = np.hstack([np.ones((X_test.shape[0],1)), X_test]) # 100 x (D + 1) vector of test inputs

# predict the function values at the test points using the maximum likelihood estimator
ml_prediction = predict_with_estimate(X_test_aug, beta_aug_ml)

# plot
plt.figure()
plt.plot(X, ynew, '+', markersize=10, label='Data')
plt.plot(X_test, ml_prediction, label='Linear Regression Fit')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.ylim(-5, 5)
plt.xlim(-5,5)
plt.legend()
plt.show()

​

​

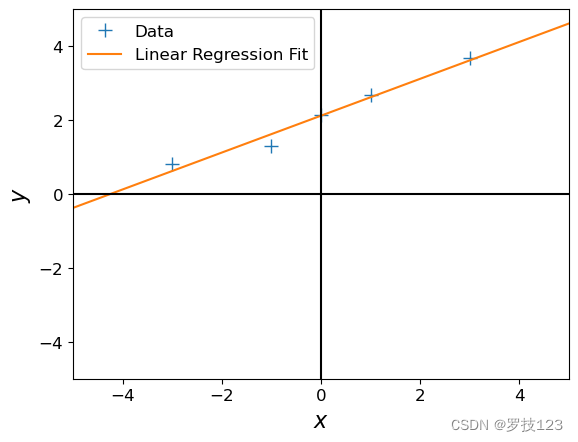
It seems this has solved our problem!

Question:

1. Play around with the first parameter of ${\mathbf{\beta }}_{\text{aug}}$ and see how the fit of the function changes.
2. Play around with the second parameter of ${\mathbf{\beta }}_{\text{aug}}$ and see how the fit of the function changes.

Section 3: Ridge regression

From our lectures, we know that ridge regression is an extension of linear regression with least squares loss function, including a (usually small) positive penalty term $\lambda$:
$$\underset{\mathbf{\beta }}{\min }\Vert \mathbf{y}-\mathbf{X}\mathbf{\beta }{\Vert }^2+\lambda \Vert \mathbf{\beta }{\Vert }^2=\underset{\mathbf{\beta }}{\min }{\text{L}}_{\text{ridge}}(\mathbf{\beta })$$
where ${\text{L}}_{\text{ridge}}$ is the ridge loss function. The solution is
$${\mathbf{\beta }}_{\text{ridge}}^{\ast }=({\mathbf{X}}^T\mathbf{X}+\lambda I{)}^{-1}{\mathbf{X}}^T\mathbf{y}.$$

This time, we will define a very small training set of only two observations to demonstrate the advantages of ridge regression over least squares linear regression.

X_train = np.array([0.5, 1]).reshape(-1,1)
y_train = np.array([0.5, 1])
X_test = np.array([0, 2]).reshape(-1,1)

Let’s define function similar to the one for least squares, but taking one additional argument, our penalty term $\lambda$.

Hint: we apply the same augmentation as above with least squares, so the offset is accurately captured.

## EDIT THIS FUNCTION
def ridge_estimate(X, y, penalty):

    # X: N x D matrix of training inputs
    # y: N x 1 vector of training targets/observations
    # returns: maximum likelihood parameters (D x 1)

    N, D = X.shape
    X_aug = np.hstack([np.ones((N,1)), X]) # augmented training inputs of size N x (D+1)
    N_aug, D_aug = X_aug.shape
    I = np.identity(D_aug)
    I[0] = 0.0 # penalty excludes the bias term.
    beta_ridge = np.linalg.solve(X_aug.T @ X_aug + penalty * I, X_aug.T @ y) ## <-- SOLUTION
    return beta_ridge

Now, we add a bit of Gaussian noise to our training set and apply ridge regression. We should do it a couple of times to be sure about the results (here 10 times).

penalty_term = 0.1
fig, ax = plt.subplots(figsize=(12, 8))
X_test_aug = np.hstack([np.ones((X_test.shape[0],1)), X_test])


for i in range(10):
    this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train

    beta_ridge = ridge_estimate(this_X, y_train, penalty=penalty_term)
    ridge_prediction = predict_with_estimate(X_test_aug, beta_ridge)

    ax.plot(X_test, ridge_prediction, color='gray',
            label='Ridge Regression Fit (on Noisy Data)' if i == 0 else '')
    ax.scatter(this_X, y_train, c='gray', marker='+', zorder=10,
               label='Noisy Data' if i == 0 else '')

beta_ridge = ridge_estimate(X_train, y_train, penalty=penalty_term)
ridge_prediction_X = predict_with_estimate(X_test_aug, beta_ridge)

ax.plot(X_test, ridge_prediction_X, linewidth=2, color='blue', label='Ridge Regression Fit')
ax.scatter(X_train, y_train, c='red', marker='+', zorder=10, label='Data')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.ylim(0, 2)
plt.xlim(0,2)
plt.legend()

<matplotlib.legend.Legend at 0x134941050>

​

​

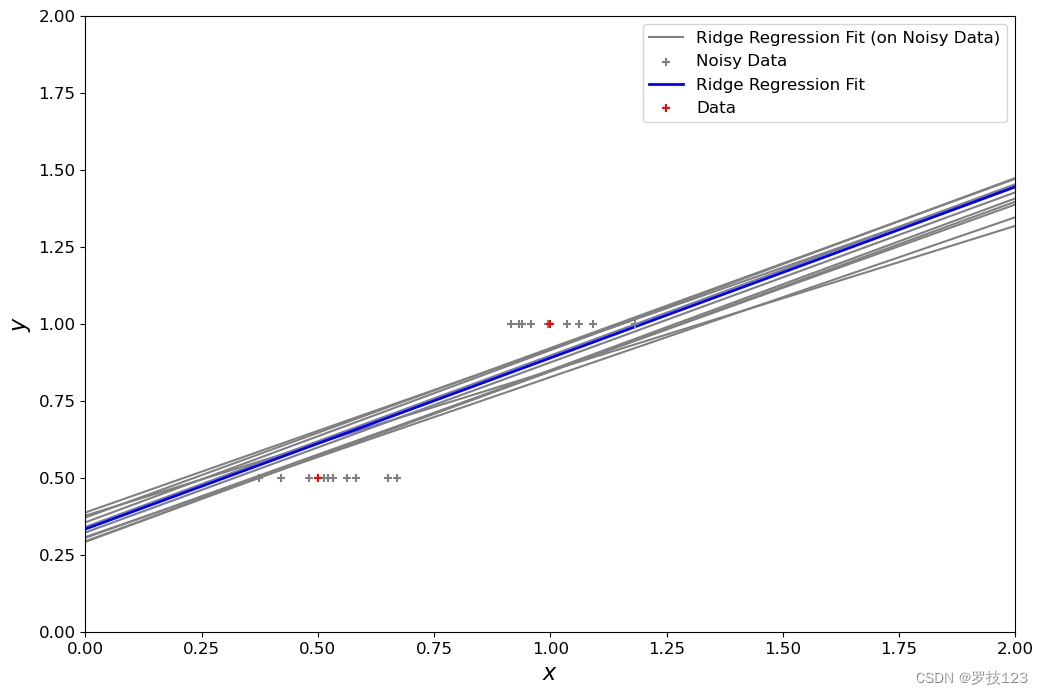
Let’s compare this to ordinary least squares:

fig, ax = plt.subplots(figsize=(12, 8))
plt.xlim(0.0, 2)
plt.ylim(0.0, 2)

X_train_aug = np.hstack([np.ones((X_test.shape[0],1)), X_train])

X_test_aug = np.hstack([np.ones((X_test.shape[0],1)), X_test])

for i in range(10):
    this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train
    N, D = this_X.shape
    this_X_aug = np.hstack([np.ones((N,1)), this_X])

    beta_aug_ml = max_lik_estimate_aug(this_X_aug, y_train)
    ml_prediction = predict_with_estimate(X_test_aug, beta_aug_ml)


    ax.plot(X_test, ml_prediction, color='gray',
            label='Unregularised Linear Regression Fit (on Noisy Data)' if i == 0 else '')
    ax.scatter(this_X, y_train, c='gray', marker='+', zorder=10,
               label = 'Noisy Data' if i == 0 else '')

beta_aug_ml = max_lik_estimate_aug(X_train_aug, y_train)
ml_prediction_X = predict_with_estimate(X_test_aug, beta_aug_ml)

ax.plot(X_test, ml_prediction_X, linewidth=2, color='blue',
        label='Unregularised Linear Regression Fit')
ax.scatter(X_train, y_train, c='red', marker='+', zorder=10,
           label='Data')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.ylim(0, 2)
plt.xlim(0,2)
plt.legend()

<matplotlib.legend.Legend at 0x13427de50>

​

​

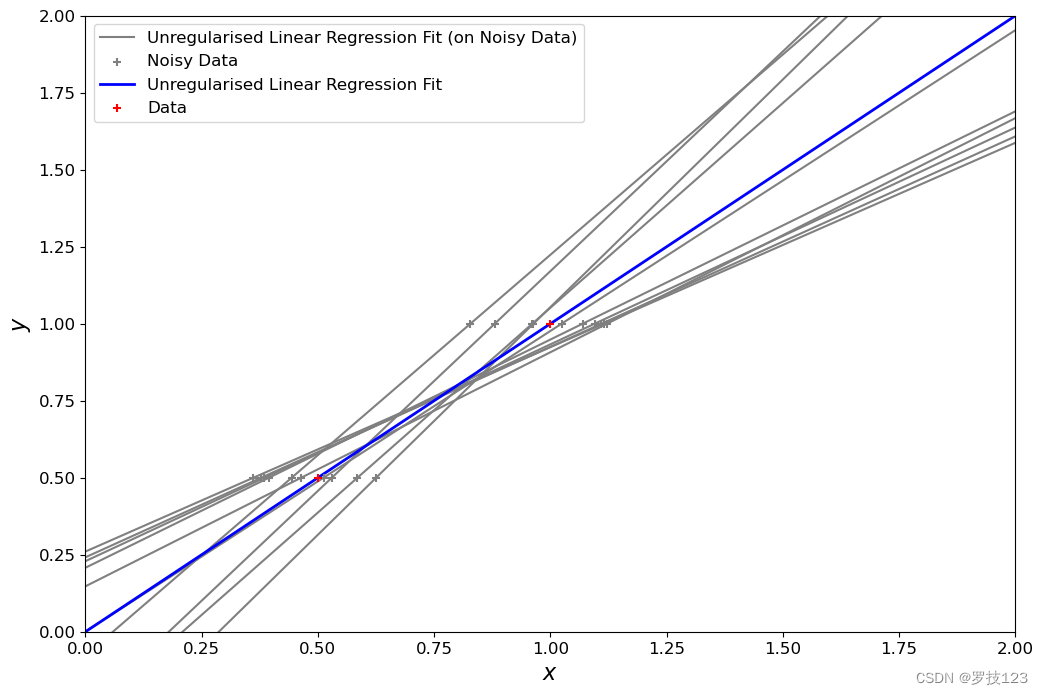
Questions

1. What differences between the two solutions above can you see?
2. Optional:
   • play around with different values of the penalty term $\lambda$. How do the corresponding functions change? Which values provide the most reasonable results?
   • Can you replicate your results using sklearn.linear_model.Ridge?
   • Based on sklearn’s documentation, can you see any differences in the algorithms that are implemented in sklearn?

Answers

1. For the standard regression, the performance on training points is very good, but can worsen on unseen test points, aka overfitting. Regularisation tends to constrain beta around more similar values, giving solutions with lower variance, but could become too close to zero with high lambda value.

penalty_term = 5
fig, ax = plt.subplots(figsize=(12, 8))
X_test_aug = np.hstack([np.ones((X_test.shape[0],1)), X_test])

for i in range(10):
    this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train

    beta_ridge = ridge_estimate(this_X, y_train, penalty=penalty_term)
    ridge_prediction = predict_with_estimate(X_test_aug, beta_ridge)

    ax.plot(X_test, ridge_prediction, color='gray',
            label='Ridge Regression Fit (on Noisy Data)' if i == 0 else '')
    ax.scatter(this_X, y_train, c='gray', marker='+', zorder=10,
               label='Noisy Data' if i == 0 else '')

beta_ridge = ridge_estimate(X_train, y_train, penalty=penalty_term)
ridge_prediction_X = predict_with_estimate(X_test_aug, beta_ridge)

ax.plot(X_test, ridge_prediction_X, linewidth=2, color='blue', label='Ridge Regression Fit')
ax.scatter(X_train, y_train, c='red', marker='+', zorder=10, label='Data')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.ylim(0, 2)
plt.xlim(0,2)
plt.legend()

<matplotlib.legend.Legend at 0x134b74dd0>

​

​

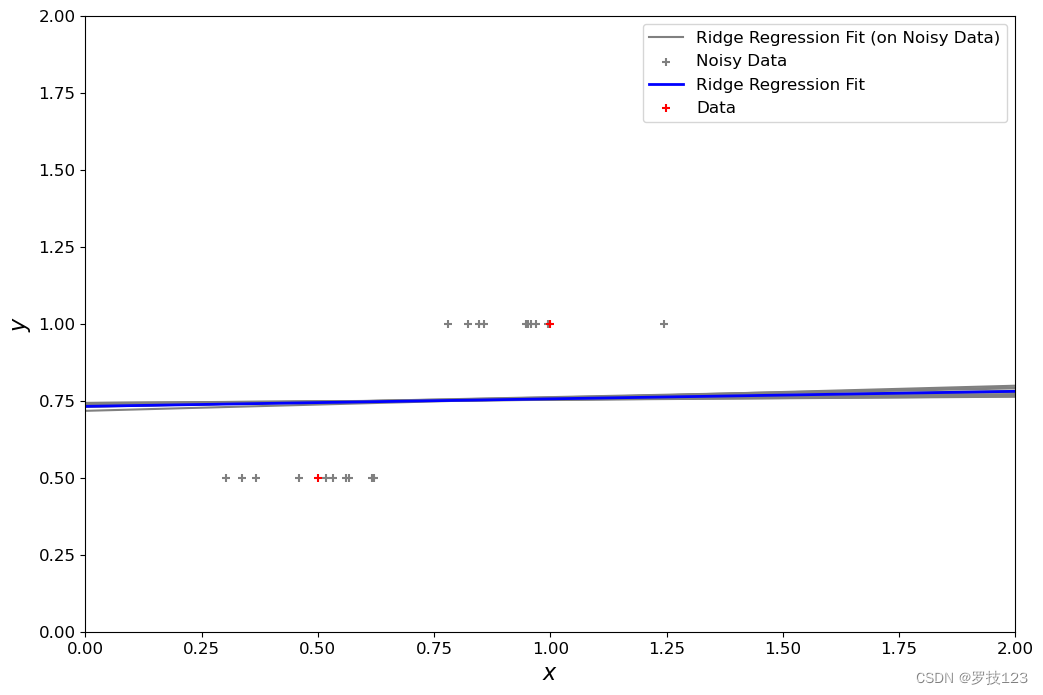
Take-Home Messages

1. Models $y={\mathbf{x}}^T\mathbf{\beta }+ϵ$ with $\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N{]}^T$ and $\mathbf{X}=[1,{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N{]}^T$ are different in terms of flexibility
2. A penalised regression with penalty term $\lambda =0$ is equivalent to the ordinary least squares regression
3. After fitting your models, check whether the plots look as expected

Section 4: LASSO regression

As opposed to the ridge regression which has a penalty term $\Vert \mathbf{\beta }{\Vert }^2$, LASSO regression introduces $ | \boldsymbol\beta |_1 $, (also known as $L_1$ loss). $L_1$ loss is often preferred if we are interested in sparse parameters, i.e. few non-zero parameters. This is generally regarded as a feature selection task, and in high-dimensional problems it helps interpret the learned parameters and their relevance.
However, no closed-form solution exists for LASSO regression as in the standard and ridge regression, so we can use the iterative gradient-descent algorithm.

In LASSO regression the aim is to minimize the following loss:

$L_{\text{LASSO}}(\mathbf{\beta })=\frac{1}{2N}||\mathbf{y}-\mathbf{X}\mathbf{\beta }|{|}^2+\lambda ||\mathbf{\beta }|{|}_1$

Where $||\mathbf{\beta }|{|}_1={\sum }_{i=1}^p|{\beta }_i|$

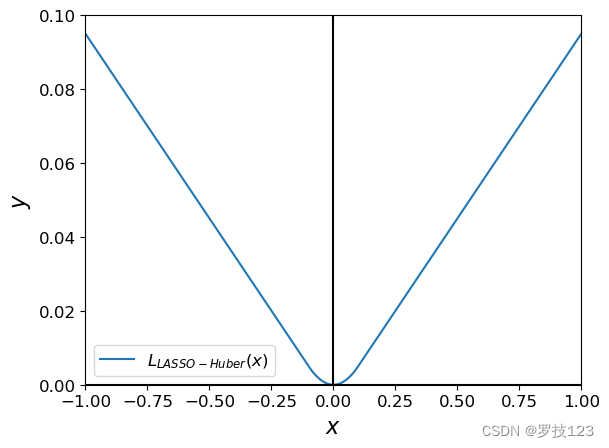
The absolute function $|.|$ adds nonsmoothness to the loss function, which can prevent the gradient-descent to converge properly to the optimal solution, and will keep bouncing around it instead. To solve this, we can use the Huber loss as an alternative to the absolute function. It combines the behaviour of $L_1$ loss except around the zero.

A relaxed optimization can be made by replacing $||\mathbf{\beta }|{|}_1$ with the Huber Loss ${\sum }_{i=1}^p{L}_c({\beta }_i)$, where $L_c(\beta )$ is defined as:

$L_c (\beta) =
\begin{cases}
\frac{1}{2}{\beta^2} & \text{for } |\beta| \le c, \
c (|\beta| - \frac{1}{2}c), & \text{otherwise.}
\end{cases}
$

The $c$ parameter in Huber determines the range around zero with $L_2$-like behaviour to ensure smoothness and, hence, better convergence.

The piecewise smooth function $L_c(\beta )$ has the gradient:

$\frac{dL_c (\beta)}{d\beta} =
\begin{cases}
\beta & \text{for } |\beta| \le c, \
c, \text{sgn}(\beta) , & \text{otherwise.}
\end{cases}
$

Now we can minimize the following relaxed function by gradient descent:

$
\begin{align} L_\text{LASSO-Huber}(\boldsymbol{\beta})
&= \frac{1}{2N}|| \boldsymbol{y} - \boldsymbol{X} \boldsymbol{\beta}||^2 + \lambda \sum_i^p L_c(\beta) \
&= \frac{1}{2N}(\boldsymbol{y} - \boldsymbol{X}\boldsymbol{\beta})^T(\boldsymbol{y} - \boldsymbol{X}\boldsymbol{\beta}) + \lambda \sum_i^p L_c(\beta) \
&= \frac{1}{2N}\left(\boldsymbol{y}^T\boldsymbol{y} - \boldsymbol{y}^T\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{\beta}^{T\boldsymbol{X}}T \boldsymbol{y} + \boldsymbol{\beta}^{T\boldsymbol{X}}T\boldsymbol{X}\boldsymbol{\beta}\right) + \lambda \sum_i^p L_c(\beta)
\end{align}
$

Which has the gradient

$
\begin{align} \nabla_\boldsymbol{\beta} L_\text{LASSO-Huber}
&= \frac{1}{N}\left(\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{X}^T\boldsymbol{y}\right) + \lambda \nabla_{\boldsymbol{\beta}}L_c(\boldsymbol{\beta})
\end{align}$

Optimization method:

• Initialize $\mathbf{\beta }$ with zeros.
• Use Gradient-descent for tuning $\mathbf{\beta }$

Implementated in Python as:

def huber(beta, c = 1e-6):
    return np.where(np.abs(beta) < c,
                    (beta**2)/2.,
                    c * (np.abs(beta) - c/2))

def grad_huber(beta, c = 1e-6):
    g = np.empty_like(beta)
    return  np.where(np.abs(beta) < c,
                    beta,
                    c * np.sign(beta))

a = np.linspace(-1, 1, 1000)
plt.plot(a, huber(a, c=0.1), label='$L_{LASSO-Huber}(x)$')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.ylim(0, 0.1)
plt.xlim(-1, 1)
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.legend()
plt.show()

​

​

a = np.linspace(-1, 1, 1000)
plt.plot(a, grad_huber(a, c=0.1), label=r'$ \nabla L_{LASSO-Huber}(x)$')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.ylim(-0.15, 0.15)
plt.xlim(-1, 1)
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.legend()

plt.show()

​

​

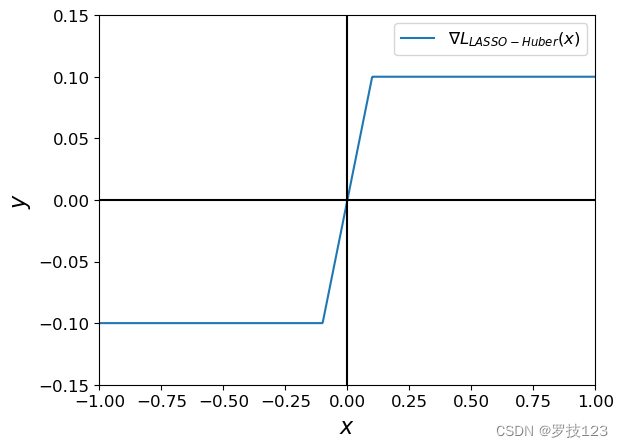
Try different $c$ values and observe the difference

Optimization with gradient-descent

We next implement gradient-descent to solve the optimisation for the LASSO model.

def minimize_ls_huber(X, y, lambd, n_iters = 10000, step_size=5e-5, c_huber=1e-4):
    """
    This function estimates the regression parameters with the relaxed version
    of LASSO regression using the gradient-descent algorithm to find the optimal
    solution.
    Args:
    X (np.array): The augmented data matrix with shape (N, p + 1).
    y (np.array): The response column with shape (N, 1).
    lambd (float): The multiplier of the relaxed L1 term.
    n_iters (int): Number of gradient descent iterations.
    step_size (float): The step size in the updating step.
    """
    n, p = X.shape
    # Precomputed products to avoid redundant computations.
    XX = X.T @ X / n
    Xy = X.T @ y / n
    # Initialize beta params with zeros
    beta = np.zeros(p)

    for i in range(n_iters):
        # Compute the gradient of the relaxed LASSO, Huber.
        grad_c = grad_huber(beta, c=c_huber)

        # Bias term is not involved in the regularisation.
        grad_c[-1] = 0 # <-- SOLUTION

        # Compute the gradient of the regularised loss.
        grad = XX @ beta -  Xy  + lambd * grad_c # <-- SOLUTION

        # Update beta
        beta = beta - step_size * grad # <-- SOLUTION

    return beta

To study the feature selection capability of LASSO, we generate a 3 dimensional synthetic data set $X$ where the second dimension does not contribute significantly to the target $y$.

np.random.seed(42)

# Generate random data with three features
X1 = np.random.rand(100)
X2 = np.random.rand(100)  # Insignificant feature (with small theta below)
X3 = np.random.rand(100)
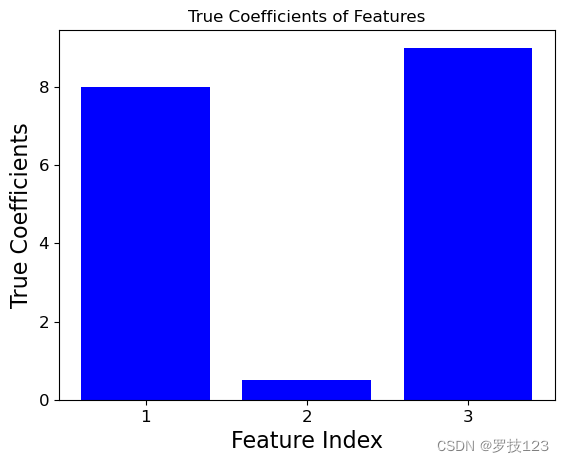
true_theta = np.array([8, 0.5, 9])  # Weights for features
y = X1 * true_theta[0] + X2 * true_theta[1] + X3 * true_theta[2] + np.random.randn(100)

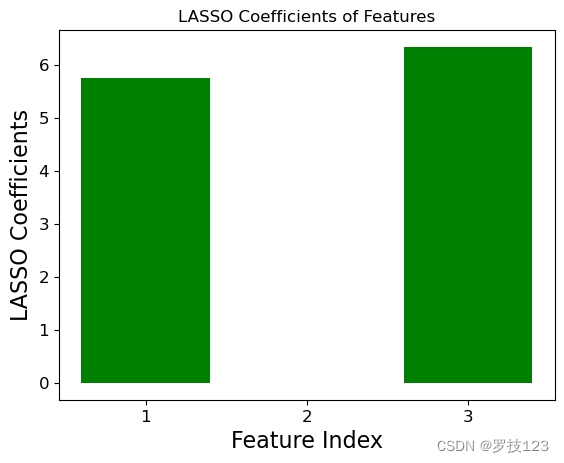
We can compare the ground truth coefficients used to create the synthetic data set to the optimal LASSO coefficients. We observe that the insignificant second feature has an optimal LASSO coefficent close to zero, and this illustrates that LASSO only selects the first and third feature as significant.

# Add bias term
X_aug = np.stack((X1, X2, X3, np.ones(100)), axis=1)

# Run LASSO regression
theta_lasso = minimize_ls_huber(X_aug, y, 5e3, n_iters=15000,
                                step_size=1e-3,
                                c_huber=1e-5)

# Print the result
print("LASSO Regression Coefficients:")
print("Theta (Intercept):", theta_lasso[3])
print("Theta 1:", theta_lasso[0])
print("Theta 2:", theta_lasso[1])
print("Theta 3:", theta_lasso[2])

LASSO Regression Coefficients:
Theta (Intercept): 2.8782141062071673
Theta 1: 5.7502057190141835
Theta 2: -0.00455907128380739
Theta 3: 6.3426969666368445

import matplotlib.pyplot as plt

for theta, label in ((true_theta, 'True'), (theta_lasso[:-1], 'LASSO')):
    plt.bar([1,2,3], theta, color='blue' if label == 'True' else 'green')
    plt.xlabel('Feature Index')
    plt.xticks([1,2,3])
    plt.ylabel(f'{label} Coefficients')
    plt.title(f'{label} Coefficients of Features')
    plt.show()

​

​

Questions

1. Try adding more insignicant variables and repeat the experiments. Do you still get the expected sparse solution? If not, what hyperparameters might need a re-tune?

2. Can you observe a clear pattern in how coefficients change as the penalty term $\lambda$ varies? Can you create a plot that shows the trajectory of each coefficient as $\lambda$ changes?

3. Optional:

   • Can you replicate your results using sklearn.linear_model.Lasso?
   • Based on sklearn’s documentation, can you see any differences in the algorithms that are implemented in sklearn?

Answers

We repeat the experiment on a five dimensional dataset $X$ where the second and fifth dimensions contribute insignicantly to the target $y$.

np.random.seed(0)

# Generate random data with five features
X1 = np.random.rand(100)
X2 = np.random.rand(100)  # Insignificant feature (with small theta below)
X3 = np.random.rand(100)
X4 = np.random.rand(100)
X5 = np.random.rand(100) # Insignificant feature (with small theta below)

true_theta = np.array([8, 0.5, 9, 4, 0.01])  # Weights for features

y = X1 * true_theta[0] + X2 * true_theta[1] + X3 * true_theta[2] +  X4 * true_theta[3] +  X5 * true_theta[4] + np.random.randn(100)
# Add bias term
X_aug = np.stack((X1, X2, X3, X4, X5, np.ones(100)), axis=1)

We can now study the effect of the penality term $\lambda$ on the LASSO coefficients.

def lasso_coefficient_trajectories(lambdas, X_aug, y):
    """Computes the trajectories of the LASSO coeffiencts for a list of lambdas.
    """
    # initialise trajectories
    coeff_trajectories = []
    for lam in lambdas:
        # Run LASSO regression
        theta_lasso = minimize_ls_huber(X_aug, y, lambd=lam, n_iters=15000,
                                        step_size=1e-3,
                                        c_huber=1e-5)
        coeff_trajectories.append(theta_lasso[:-1])
    return np.vstack(coeff_trajectories)

# define range for lambdas
lambdas = np.logspace(-5, 5, 40)

# compute the trajectories of LASSO coefficients
coeffs = lasso_coefficient_trajectories(lambdas, X_aug, y)

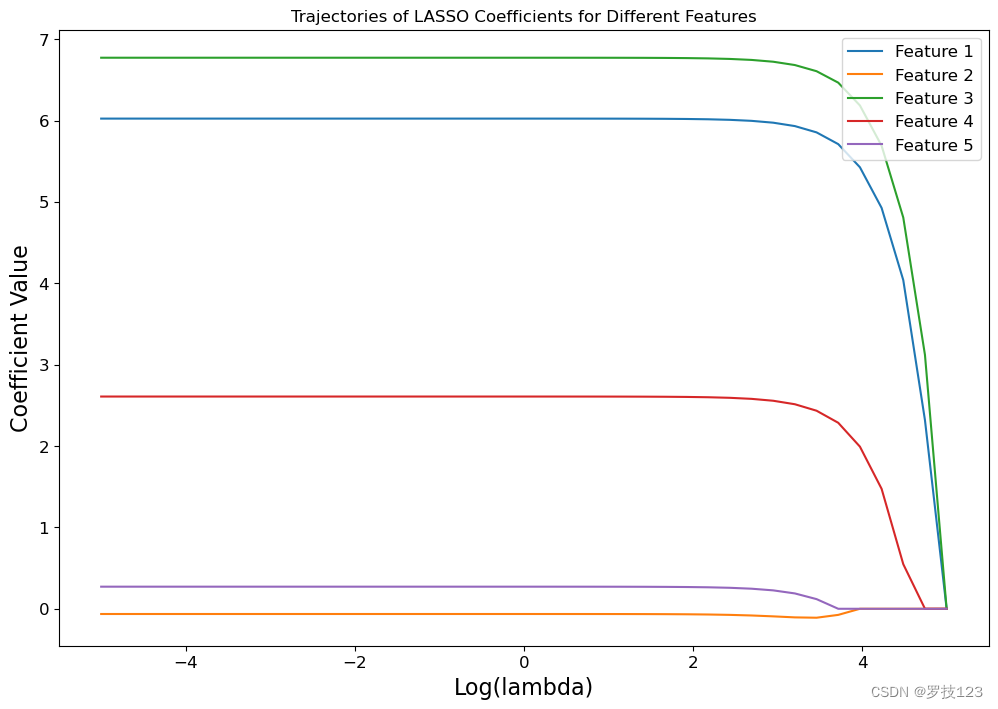
Plotting the trajectories of the LASSO coefficients for the 5 different features below shows us that the insiginifcant features 2 and 5 are always assigned LASSO coefficients close to zero. Only when the regularization is very strong, i.e., for large values of $\lambda$, all coefficients are pushed towards zero.

# plot the trajectores of LASSO coefficients using log-scale
plt.figure(figsize=(12, 8))
for i in range(coeffs.shape[1]):
    plt.plot(np.log10(lambdas), coeffs[:, i], label=f'Feature {i + 1}')

plt.xlabel('Log(lambda)')
plt.ylabel('Coefficient Value')
plt.title('Trajectories of LASSO Coefficients for Different Features')
plt.legend()
plt.show()

​

​