【中心】不规则多边形中心、形心、外接矩形中心计算方法

every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog

0. 前言

不规则多边形 中心、形心、外接矩形中心 计算方法

1. 正文

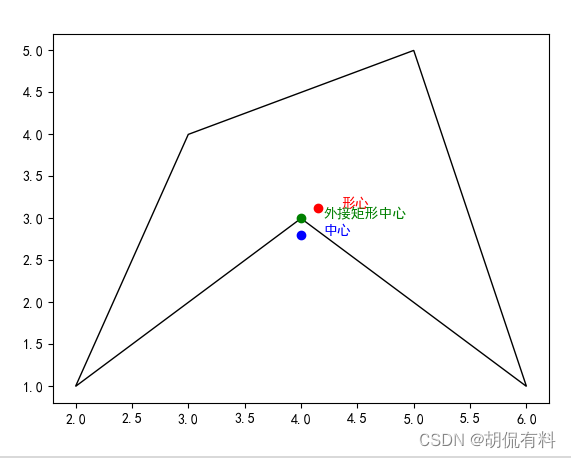
1.1 中心

# 多边形中心
center = np.mean(vertices, axis=0)

1.2 形心

形心的若干种计算方法：https://blog.csdn.net/weixin_39190382/article/details/131780577?spm=1001.2014.3001.5502

polygon = Polygon(vertices)
centerx = polygon.centroid.x
centery = polygon.centroid.y

1.3 外接矩形中心

def calculate_bounding_rectangle_center(vertices):
    # 提取顶点坐标中的 x 和 y 分量
    x_coords, y_coords = zip(*vertices)

    # 计算顶点坐标的最小和最大值
    min_x = min(x_coords)
    max_x = max(x_coords)
    min_y = min(y_coords)
    max_y = max(y_coords)

    # 计算外接矩形的中心坐标
    center_x = (min_x + max_x) / 2
    center_y = (min_y + max_y) / 2

    return center_x, center_y

1.4 完整代码

import numpy as np
from shapely.geometry import Polygon
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 图中文字体设置为黑体
plt.rcParams['axes.unicode_minus'] = False  # 负值显示

# 设置中文字体
# 定义凹多边形的顶点坐标
# vertices = [(2, 1), (4, 3), (6, 1), (5, 5), (3, 4)]
# vertices = [(1, 1), (3, 2), (5, 4), (4, 6), (2, 5)]
# vertices = [(1, 1), (3, 2), (5, 4), (4, 6), (2, 5)]
# vertices = [(1, 1), (1, 2), (5, 2), (5, 1)]
# 定义月牙形状多边形的顶点坐标
# vertices = [(1, 1), (2.5, 0), (4, 1), (4, 3), (2.5, 4), (1, 3)]
# vertices = [(1, 2), (3, 4), (5, 4), (7, 2), (6, 0), (2, 0)]
vertices = [(2, 1), (4, 3), (6, 1), (5, 5), (3, 4)]


def calculate_bounding_rectangle_center(vertices):
    # 提取顶点坐标中的 x 和 y 分量
    x_coords, y_coords = zip(*vertices)

    # 计算顶点坐标的最小和最大值
    min_x = min(x_coords)
    max_x = max(x_coords)
    min_y = min(y_coords)
    max_y = max(y_coords)

    # 计算外接矩形的中心坐标
    center_x = (min_x + max_x) / 2
    center_y = (min_y + max_y) / 2

    return center_x, center_y


# 多边形中心
center = np.mean(vertices, axis=0)

# d外接矩形中心
cc = calculate_bounding_rectangle_center(vertices)

polygon = Polygon(vertices)
centerx = polygon.centroid.x
centery = polygon.centroid.y

plt.figure()
polygon = plt.Polygon(vertices, fill=None, edgecolor='black')
plt.gca().add_patch(polygon)

plt.scatter(center[0], center[1], color='blue')
plt.annotate('中心', xy=(center[0], center[1]), xytext=(
    center[0]+0.2, center[1]), color='blue')

plt.scatter(centerx, centery, color='red')
plt.annotate('形心', xy=(centerx, centery),
             xytext=(centerx+0.2, centery), color='red')

plt.scatter(cc[0], cc[1], color='green')
plt.annotate('外接矩形中心', xy=(cc[0], cc[1]),
             xytext=(cc[0]+0.2, cc[1]), color='green')
plt.show()

参考

[1] https://blog.csdn.net/weixin_39190382/article/details/131780577?spm=1001.2014.3001.5502