快速排序详解

理解原理

快速排序在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成了两个部分。

这种思路就叫做分治法。

每次把数列分成两部分，究竟有什么好处呢？

假如给定8个元素的数列，一般情况下冒泡排序需要比较8轮，每轮把一个元素移动到数列一端，时间复杂度是O（n^2）。

而快速排序的流程是什么样子呢？

如图所示，在分治法的思想下，原数列在每一轮被拆分成两部分，每一部分在下一轮又分别被拆分成两部分，直到不可再分为止。

这样一共需要多少轮呢？平均情况下需要logn轮，因此快速排序算法的平均时间复杂度是 O（nlogn）。

基准元素的选择

基准元素，英文pivot，用于在分治过程中以此为中心，把其他元素移动到基准元素的左右两边。

那么基准元素如何选择呢？

最简单的方式是选择数列的第一个元素：

这种选择在绝大多数情况是没有问题的。但是，假如有一个原本逆序的数列，期望排序成顺序数列，那么会出现什么情况呢？

极端情况：逆序的数列 N^2

解决方法： 随机选择一个元素作为基准元素。

当然，即使是随机选择基准元素，每一次也有极小的几率选到数列的最大值或最小值，同样会影响到分治的效果。

所以，快速排序的平均时间复杂度是 O（nlogn），最坏情况下的时间复杂度是 O（n^2）。

元素的移动

我们要做的就是把其他元素当中小于基准元素的都移动到基准元素一边，大于基准元素的都移动到基准元素另一边。

1.挖坑法

.

.

.

挖坑法代码

public class QuickSort {
	
	public static void main(String[] args) {
		
		int[] arrays = {12,21,3,5,2,18,7,4,11,9,12};
		System.out.println("快速排序之挖坑排序前的数组:" +Arrays.toString(arrays));
		pothlingSort(arrays, 0 , arrays.length - 1);
		System.out.println("快速排序之挖坑排序后的数组:" +Arrays.toString(arrays));
	}
	
	/**
	 * 挖坑法
	 * @param arrays
	 * @param low
	 * @param high
	 */
	public static void pothlingSort(int[] arrays , int low , int high){
		
 
		if(low < high){
		
		//求每次分治的分割线
		int divideIndex = getDivideIndex(arrays,low,high);
		//再递归分别对分割的俩个子数组进行递归排序
		pothlingSort(arrays,low,divideIndex -1);
		pothlingSort(arrays,divideIndex + 1, high);
	}
 
}
 
	private static int getDivideIndex(int[] arrays, int low, int high) {
		int pivot = array[low];
        int left = low;
        int right = hight;
        int index = low;

        while (right >= left){
            
            while(right >= left){
                if (array[right] < pivot){
                    array[left] = array[right];
                    index = right;
                    left++;
                    break;
                }
                right--;
            }
            
            while(right >= left){
                if(array[left] > pivot){
                    array[right] = array[left];
                    index = left;
                    right --;
                    break;
                }
                left++;
            }





        }
}

 

2.指针交换法

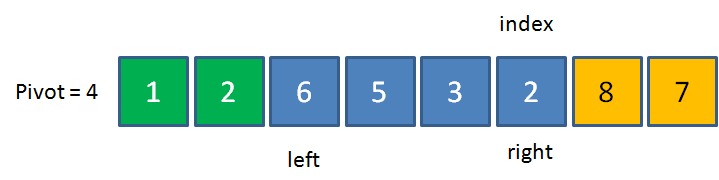
我们首先选定基准元素Pivot，并且设置两个指针left和right，指向数列的最左和最右两个元素：

由于7 > 4，left指针在元素7的位置停下。这时候，我们让left和right指向的元素进行交换。

接下来，我们进入第二次循环，重新切换到right向左移动。right先移动到8，8>4，继续左移。由于2<4，停止在2的位置。

切换到left，6>4，停止在6的位置。

元素6和2交换。

.

.

.

进入第四次循环，right移动到元素3停止，这时候请注意，left和right指针已经重合在了一起。

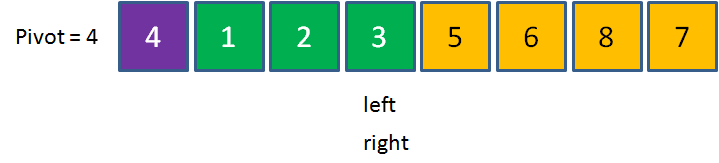
当left和right指针重合之时，我们让pivot元素和left与right重合点的元素进行交换。此时数列左边的元素都小于4，数列右边的元素都大于4，这一轮交换终告结束。

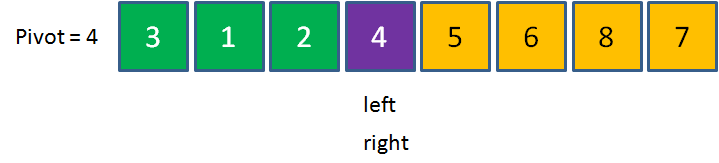
package com.Jevin.priorityQueue;
 
public class QuickSort {
    
    public static void quickSort(int[] arr,int low,int high){
        int i,j,temp,t;
        if(low>high){
            return;
        }
        i=low;
        j=high;
        //temp就是基准位
        temp = arr[low];
 
        while (i<j) {
            //先看右边，依次往左递减
            while (temp<=arr[j]&&i<j) {
                j--;
            }
            //再看左边，依次往右递增
            while (temp>=arr[i]&&i<j) {
                i++;
            }
            //如果满足条件则交换
            if (i<j) {
                t = arr[j];
                arr[j] = arr[i];
                arr[i] = t;
            }
 
        }
        //最后将基准为与i和j相等位置的数字交换
        arr[low] = arr[i];
        arr[i] = temp;
        //递归调用左半数组
        quickSort(arr, low, j-1);
        //递归调用右半数组
        quickSort(arr, j+1, high);
    }
 
 
    public static void main(String[] args){
        int[] arr = {7,10,2,4,7,1,8,5,19};
        quickSort(arr, 0, arr.length-1);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
    }
}