Median of Two Sorted Arrays

问题描述

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

两个已排序的数组大小为m的nums1和大小为n的nums2。

找到两个排序数组的中位数，整体的运行时间复杂度应该为 O(log (m+n))。

可以假设nums1和nums2不能同时为1

样例

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

解题思路

本题为找中位数，中位数在排序数组元素为偶数时，为最中间两个数的平均值。在数组元素个数为奇数时，为排序后最中间元素的值。本题的难点为，如何将两个未合并的数组求出他们的中位数。

思路一 ：merge+sort

最一般的想法为，先将两个数组合并排序后查找中位数。如果合并后元素数m+n为奇数，则 m+n+1/2 为中位数； 如果m+n为偶数，则中位数为(m+n/2+m+n+2/2)/2但是显然这种方法的时间复杂度为合并数组后的排序的时间复杂度。拿快速排序为例，为O（m+n）。不符合题目要求。但是leetcode还是过了，看来leetcode对时间复杂度没有要求。

python3代码

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        a = nums1+nums2
        a.sort()
        half=int(len(a)/2)
        if((len(a)%2)!= 0):
            return a[half]
        else:
            return (a[half-1]+a[half])/2

思路二：第k最小值

上述中位数的求法其实可以概括为求（m+n+1)/2, (m+n+2)/2 两个数的平均值。

1）m+n为偶数时 （m+n+1)/2 == （m+n)/2

2）m+n为奇数时 （m+n+1)/2 == (m+n+2)/2

所以只需求第(m+n+1)/2和(m+n+2)/2位的数即可。问题转换为“如何求第k小的数“的问题。

题目要求O(log(m+n)), 很自然的想到要用二分法。那么如何二分，对谁二分是需要关注的问题。

在这个方法中，我们要二分的对象是K。基本思路如下，将k二分为k/2。找到两个数组中的k/2，k-k/2的数据比较大小。因为要找第k个最小值，小的那组前k/2或者k-k/2个数据显然不可能是第k个数据。所以可以将那组前k/2个数删掉。

接下来考虑极限情况。

① 一个数组为空，直接在另一个数组中找中位数。

② 当k==1时，即要找的数排在第一位时，也就是说最小时，比较两个最小值谁更小，谁就为中位数。

例如，两个数组nums1[1,3,5,7], nums2[2,4,6,8,9]。

第一轮：

​ k=m+n+1/2=5

​ k/2=2; k-k/2=3

​ 我们在两个数组中找到(nums1[1]==3) < (nums2[2]==6)，所以nums1前2个可以舍弃。

第二轮：

​ 变为nums1[5,7], nums[2,4,6,8,9]。

​ k=5-2=3

​ k/2=1; k-k/2=2

​ 我们在两个数组中找到(nums1[0]==5) > (nums2[2]==4)，所以nums2前2个可以舍弃。

第三轮：

​ 变为nums1[5,7], nums[6,8,9]。

​ k=3-2=1

​ min(nums1[0],nums2[0])=5

代码如下：这个版本为

C++

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size(), left = (m+n+1)/2, right = (m+n+2)/2;
        return (findKth(nums1,0,nums2,0,left)+findKth(nums1,0,nums2,0,right))/2.0;
    }
    double findKth(vector<int>& nums1, int i, vector<int>& nums2, int j, int k){
        if(i>=nums1.size())
            return nums2[j+k-1];
        if(j>=nums2.size())
            return nums1[i+k-1];
        if(k==1)
            return min(nums1[i],nums2[j]);
        int midVal1 = (i+k/2-1<nums1.size())?nums1[i+k/2-1]:INT_MAX;
        int midVal2 = (j+k-k/2-1<nums2.size())?nums2[j+k-k/2-1]:INT_MAX;
        if(midVal1<midVal2){
            return findKth(nums1,i+k/2,nums2,j,k-k/2);
        }else{
            return findKth(nums1,i,nums2,j+k-k/2,k/2);
        }
    }
};

JAVA

与C++ 版本不同的是，在这里没记录数组下标，而是选择每次构造两个新的数组。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m=nums1.length, n=nums2.length, left=(m+n+1)/2,right=(m+n+2)/2;
        return (findKth(nums1,nums2,left)+findKth(nums1,nums2,right))/2.0;
    }
    public double findKth(int[] nums1, int[] nums2, int k){
        int m = nums1.length, n= nums2.length;
        if(m==0) return nums2[k-1];
        if(n==0) return nums1[k-1];
        if(k==1) return Math.min(nums1[0],nums2[0]);
        int i=Math.min(m,k/2), j=Math.min(n,k-i);
        if(nums1[i-1]<nums2[j-1]){
            return findKth(Arrays.copyOfRange(nums1,i,m),nums2,k-i);
        }
        else{
            return findKth(nums1,Arrays.copyOfRange(nums2,j,n),k-j);
        }
        
    }
}

思路三：二分查找

思路建议观看这个视频。但是视频里有个错误在7:18，end应该为5，不是4。

基本思路就是，将两个数组各分为两部分，保证两个数组的左半部分的联合都小于右边的数字联合，且左右划分对称。举个栗子。

有两个升序数组A，B

A [$x_1$,$x_2$,$x_3$,$x_4$,$x_5$,$x_6$]

B [$y_1$,$y_2$,$y_3$,$y_4$,$y_5$,$y_6$,$y_7$,$y_8$]

加入A、B可以如下划分。| 代表划分

A [$x_1$,$x_2$|$x_3$,$x_4$,$x_5$,$x_6$]

​ 2 4

B [$y_1$,$y_2$,$y_3$,$y_4$,$y_5$|$y_6$,$y_7$,$y_8$]

​ 5 3

数组A，B的左边的所有数字的个数等于右边的个数。假如$x_2<y_6,y_5<x_3$，我们就可以说中位数一定是$median=average(max(x_2,y_5),min(x_3,y_6))$。

所以我们要找到对于长度短的数组的一个合适的划分。这个划分要满足两个条件。

① 两个数组左边的所有数都要小于等于右边所有的数。想象把划分左边的都装一个袋子里，右边装另一个袋子里。

② 两个数组左边的所有元素的个数与右边相等

中位数的两种情况

这样我们在找到满足条件的划分后，A数组划分左右两边的称为L1，R1；B的划分两边称为L2，R2。

① 在总长度为基数时中位数为$median=average(max(L_1,L_2）,min(R_1,R_2))$。

② 总长度为偶数时 $median=max(L1,L2)$。

伪代码如下：

partitionX+pertitionY=(n+m+1)/2
Found:
	MAXleftX<=MINrightY
	MAXleftY<=MINleftY
else if:
	MAXleftX>MINright
	move towards left in X
else:
	move towards right in X

举个实例讲解一下

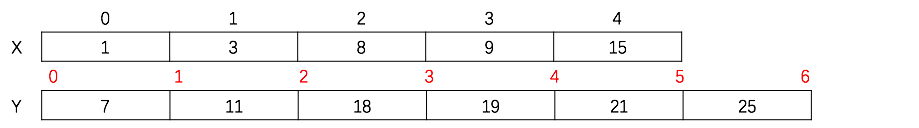
两个数组X [1,3,8,9,15], Y[7,11,18,19,21,25], 求的目标为中位数11

按照基本思路，对短的数组X进行划分，总共有五种划分办法。

所以 start=0， end=5，partitonX=(start+end)/2=2, partitionY= (X+Y+1)/2-partitionX=3

我们在X的2（红色的2）处划分，Y的3处划分，

1 3 | 8 9 15

7 11 18 | 19 21 25

L1=3 R1=8 L2=18 R2=19

L2>R2 所以partitionX要往右移

strat=partitionX+1=3 end=5 partitionX=(3+5)/2=4 partitionY=(5+6+1)/2-4=2

1 3 8 9| 15

7 11| 18 19 21 25

L1=9 R1=15 L2=11 R2=18

L1<R2, L2<R1 满足条件

因为 X+Y=11 为奇数，median=max(L1,L2)=11

极限情况中，X或Y左边可能不包含元素的情况下 ，取最小值；X或Y右边不包含元素，取最大值。

C++

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size(), m = nums2.size();
        if (n>m) return findMedianSortedArrays(nums2,nums1);//make sure nums1 is shorter one
        
        int start=0, end = n, K = (n+m+1)/2;
        while(start <= end){
            double a = (start + end)/2, b = K -a;//a is partition of nums1, b is partition of nums2
            
            double L1 = (a==0)?INT_MIN:nums1[a-1];
            double L2 = (b==0)?INT_MIN:nums2[b-1];
            double R1 = (a==n)?INT_MAX:nums1[a];
            double R2 =  (b==m)?INT_MAX:nums2[b];
            
            if (L1>R2) end = a-1;
            else if(L2>R1) start = a+1;
            else{
                if((n+m)%2!=0){
                    return max(L1,L2);
                }
                else{
                    return (min(R1,R2)+max(L1,L2))/2.0;
                }
            }              
            
        }
        return -1;
    }
};