NLP学习__task4：传统机器学习：朴素贝叶斯、SVM、PLSA、LDA

士416

已于 2023-05-14 17:22:19 修改

阅读量2k

点赞数 2

分类专栏：机器学习文章标签：朴素贝叶斯 SVM PLSA LDA

于 2019-03-09 17:55:32 首次发布

本文链接：https://blog.csdn.net/weixin_39441762/article/details/88356998

版权

机器学习专栏收录该内容

20 篇文章 3 订阅

订阅专栏

1、朴素贝叶斯的原理

在所有机器学习分类算法中，朴素贝叶斯和其他绝大多数分类算法不同。不同于：例如决策树、KNN、逻辑回归、支持向量机等，这些都是判别方法，即直接学习出特征输出Y和特征X之间的关系，也是决策数 $Y=f(X)$ ；而朴素贝叶斯是生成方法，即直接找出特征输出Y和特征X的联合分布 $P(X,Y)$ ，然后用 $P(Y|X)=P(X,Y)/P(X)$ 得出。

1）朴素贝叶斯的定理

首先，明确贝叶斯统计方式与统计学中的频率概念不同：从频率的角度出发，即假定数据遵循某种分布，我们的目标是确定该分布的几个参数，在某个固定的环境下做模型；贝叶斯则是根据实际的推理方式来建模，用训练数据来更新模型对某件事即将发生的可能性的预测结果，即有对于一个样本有这些特征的情况下是某一类别的可能性有多大。

贝叶斯定理旨在计算 $P(Y|X)$ 的值，即在知道X发生的情况下，Y发生的概率是多少。大多数情况下，X是被观察事件，比如“上午乌云密布”，Y预测结果“一会儿会下雨”。对于数据挖掘来说，X通常是观察样本个体的特征，Y为样本个体所属的类别。简言之，贝叶斯就是计算：样本X特征是Y类别的概率。

2）朴素贝叶斯的模型

朴素贝叶斯假设：(1) 特征独立；(2) 基于贝叶斯定理。

根据贝叶斯定理，对于一个分类问题，给定样本特征x，样本属于类别y的概率是

$p(y|x)=\frac{p(x|y)p(y)}{p(x)}$

在这里，x是一个特征向量，将设x维度为M。因为朴素的假设，即特征条件独立，根据全概率公式展开，公式可以表达为：

$p(y=c_{k}|x)=\frac{\prod _{i=1}^{M}p(x_{i}|y=c_{k})p(y=c_{k})}{\sum _{k}p(y=c_{k})\prod _{i=1}^{M}P(x^{i}|y=c_{k})}$

因此，估计出特征在每一类的条件概率，选择概率最大即可知道特征所属的类别。对于类别y的先验概率 $(p(y=c_{k}))$ 可以通过训练集算出，同样通过训练集上的统计，可以得出对应每一类上的，条件独立的特征对应的条件概率向量。由于分母中为全概率 $(p(x^{i}|y=c_{k}))$ 可视为常数，实际可不计算。

如果从样本中算出的概率值为0应该怎么办呢？下面引入拉普拉斯平滑方法，解决这一问题。给学习步骤中的两个概率计算公式，分子和分母都分别加上一个常数，就可以避免这个问题。更新过后的公式如下：

$p(y=c_{k})=\frac{\sum _{i=1}^{N}I(y_{i}=c_{k})+\lambda }{N+K\lambda }$

K是类的个数

$p(x^{j}=a_{jl}|y=c_{k})=\frac{\sum _{i=1}^{N}I(x_{i}^{j}=a_{jl},y_{i}=c_{k})+\lambda }{\sum _{i=1}^{N}I(y_{i}=c_{k})+L_{j}\lambda }$

$L_{j}$ 是第j维特征的最大取值。

(这篇博客对朴素贝叶斯公式具体如何分类进行了具体例子的计算：浅谈朴素贝叶斯算法原理)

3）朴素贝叶斯中常见的模型

朴素贝叶斯分类器属于有监督学习方法，常见的模型有：多项式模型(multinomial model，即词频型)和伯努利模型(Bernoulli model，即文档型)，还有高斯模型。

多项式模型和伯努利模型的计算粒度不一样，多项式模型以单词为粒度，伯努利模型以文件为粒度，因此二者的先验概率和类条件概率的计算方法都不同。计算后验概率时，对于一个文档d，多项式模型中，只有在d中出现过的单词，才会参与后验概率计算，伯努利模型中，没有在d中出现，但是在全局中单词表中出现的单词，也会参与计算，不过作为“反方”参与的。

2、利用朴素贝叶斯模型进行文本分类

根据上面所提及的三种模型：多项式模型、伯努利模型，对cnews.train.txt文件中的文本进行分类处理和预测。此处仅作为测试，所以仅使用部分数据来做训练和预测。

1）多项式模型

在多项式模型中，设某文档 $d=(t_{1},t_{2},...,t_{k}),t_{k}$ 是该文档中出现过的单词，允许重复，则先验概率

$P(y=c_{k})=\frac{sumC_{k}}{\sum _{i=1}^{K}sumC_{i}}$

其中： $sumC_{k}$ 表示类别k下单词总数， $\sum _{i=1}^{K}sumC_{i}$ 表示整个训练样本的单词总数。

类条件概率 $P(t_{k}|c)$ =(类c下单词 $t_{k}$ 在各个文档中出现过的次数之和+1)/(类c下单词总数+|v|)。其中V是训练样本的单词表(即抽取单词，单词出现多次，只计算一个)，|V|则表示训练样本包含多少种单词。 $P(t_{k}|c)$ 可以看作是单词 $t_{k}$ 在证明d属于类c上提供了多达的证据，而 $p(c)$ 则可以认为是类别c在整体上占有多大比例。

2）伯努利模型

P(c)= 类c下文件总数/整个训练样本的文件总数
P(tk|c)=(类c下包含单词tk的文件数+1)/(类c下包含的文件+2)

(详细内容可见：【二十】机器学习之路——朴素贝叶斯实战(文本分类))

根据多项式模型和伯努利模型对文本进行分类，其demo如下(或者：朴素贝叶斯分类)：

import jieba
import pandas as pd
import numpy as np
from sklearn.feature_extraction.text import TfidfTransformer,CountVectorizer
from sklearn.naive_bayes import MultinomialNB,BernoulliNB
import random

# preprocess用于将一个文本文档进行切词，并以字符串形式输出切词结果
path = './cnews.test.txt'
with open(path,'r',encoding='UTF-8') as f:
    cnews_test = f.readlines()
# 取test中前3000出来分为2000为训练样本，1000测试样本
cnews_test = cnews_test[500:1000]+cnews_test[1500:2000]+cnews_test[2500:3000]+cnews_test[3500:4000]+cnews_test[4500:5000]+cnews_test[5500:6000]
# 将test中的label取出
test_label,test_x = [],[]
n = list(range(len(cnews_test)))
random.shuffle(n)
for i in n:
    each = cnews_test[i]
    each0 = each.split('\t')
    test_label.append(each0[0])
    test_x.append(each0[1])

# 取test中前3000出来分为2000为训练样本，1000测试样本
import jieba
# 使用jieba精确分词
test_x = [[each0 for each0 in jieba.cut(each)] for each in test_x]
test_x = [' '.join(each) for each in test_x]

# 将3000个样本分为2500的train数据，500的test数据
train_X = test_x[:2500]
train_y = test_label[:2500]
test_X = test_x[2500:]
test_y = test_label[2500:]

# 多项式模型计算文本分类
count_vector = CountVectorizer()
# 该类会将文本中的词语转换为词频矩阵，矩阵元素a[i][j]表示j词在i类文本下的词频
vector_matrix = count_vector.fit_transform(train_X)

# tfidf度量模型
train_tfidf = TfidfTransformer(use_idf=False).fit_transform(vector_matrix)
# 将词频矩阵转化为权重矩阵，每一个特征值就是一个单词的TF-IDF值

# 调用MultinomialNB分类器进行训练
clf = MultinomialNB().fit(train_tfidf,train_y)

# 测试
test_vector = count_vector.transform(test_X)
test_tfidf = TfidfTransformer(use_idf=False).fit_transform(test_vector)
predict_result = clf.predict(test_tfidf)

# 以正确分类的个数，简单评测模型预测结果的准确率
# 评测预测效果
def accuracy_(test_y,predict):
    TP,num = 0,len(test_y)
    for i in range(num):
        if test_y[i]==predict[i]:
            TP+=1
    return TP/num

# 多项式模型分类效果
print('多项式模型分类效果：%f'%accuracy_(test_y,predict_result))
# 结果：多项式模型分类效果：0.970000

# 伯努利模型计算文本分类
count_vector = CountVectorizer()
# 该类会将文本中的词语转换为词频矩阵，矩阵元素a[i][j]表示j词在i类文本下的词频
vector_matrix = count_vector.fit_transform(train_X)

# tfidf度量模型
train_tfidf = TfidfTransformer(use_idf=False).fit_transform(vector_matrix)
# 将词频矩阵转化为权重矩阵，每一个特征值就是一个单词的TF-IDF值

# 调用MultinomialNB分类器进行训练
clf = BernoulliNB().fit(train_tfidf,train_y)

# 测试
test_vector = count_vector.transform(test_X)
test_tfidf = TfidfTransformer(use_idf=False).fit_transform(test_vector)
predict_result = clf.predict(test_tfidf)

# 伯努利模型分类效果
print('伯努利模型分类效果：%f'%accuracy_(test_y,predict_result))
# 伯努利模型分类效果：0.870000

3、SVM的原理

SVM(Support Vector Mac)称支持向量机，是一种二分类的模型。修改之后可用于多分类模型。支持向量机可以分为线性和非线性两大类。其主要思想为找到空间中的一个更够将所有数据样本划开的超平面，并且使得在一个平面的样本点距离另一个平面的样本点距离最大。

1）线性SVM

如图是一个线性可分的二分类问题：

上图中的(a)是已有的数据，红色和蓝色分别代表两个不同的类别。数据显然是线性可分的，但是将两类数据点分开的直线显然不止一条。上图的(b)和(c)分别给出了B、C两种不同的分类方案，其中黑色实线为分界线，术语称为“决策面”。每个决策面对应了一个线性分类器。虽然从分类结果上看，分类器A和分类器B的效果是相同的。但是他们的性能是有差距的，看下图：

在”决策面”不变的情况下，添加了一个红点。可以看到此时(b)分类的效果要好于(c)；而SVM算法认为分类器(b)分类间隔比分类器(c)的分类间隔大，所以(b)的效果好于(c)。这里涉及到第一个SVM独有的概念”分类间隔”。在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优决策面（有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为”支持向量”。

上述参考博客：SVM原理篇之手撕SVM

2）非线性SVM

对于无法进行线性分割的样本，一般情况下，会将这样的样本特征映射到一个更高维的空间，再进行划分样本；而这个特征映射的函数称为核函数，整个过程称之为非线性SVM分类。

核函数是特征转换函数。在线性SVM分类中，目标是找出合适的参数w,b，使得分割得超平面间距最大，且能正确对数据进行分类。间距最大是我们得优化目标。对数据分类得是约束条件。即在满足约束条件 $y^{(i)}(w^{T}x^{(i)}+b)\geq 1$ 的前提下，求解 $\left \| w \right \|^{2}$ 的最小值。

拉格朗日乘子法是解决约束调价将那些求函数极值的理想方法。其方法是引入飞赴系数 $\alpha$ 来作为约束条件的权重：

$L=\frac{1}{2}\left \| w \right \|^{2}-\sum _{i=1}^{m}\jmath _{i}(y^{(i)}(w^{T}x^{(i)}+b)-1)$

由于极值的偏导数为0，因此这需要让L对w求导使之为0得到w和α对关系：

$w = \sum _{i=1}^{m}\alpha _{i}y^{(i)}x^{(i)}$

接着继续求L对b对偏导数得出:

$\sum _{i=1}^{m}y^{(i)}\alpha _{i}=0$

把这两个式子代入L通过数学运算得出：

$L=\sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha _{i}\alpha _{j}y^{(i)}y^{(j)}x^{(i)T}x^{(j)}$

这个公式中m是数据集个数， $\alpha$ 是拉格朗日乘子法引入的一个系数，针对数据集中的每个样本 $x^{(i)}$ ,都有对应的 $\alpha _{i}$ 。 $x^{(i)}$ 是数据集中地i个样本的输入，它是一个向量， $y^{(i)}$ 是对应的输出标签.

这个公式的最小值求解这里就不说明了。最后求出的 $\alpha$ 有个明显的特点。即大部分 $\alpha_{i}=0$ 。因为只有那些支持向量所对应的样本直接决定了间隙的大小。实际上以上推导出这个公式就是为了引入支持向量机的另外一个核心概念：核函数:

$K(x^{(i)},x^{(j)})=x^{(i)T}x^{(j)}$

L里的 $x^{(i)T}x^{(j)}$ 部分，其中 $x^{(i)}$ 是一个特征向量，所以 $x^{(i)T}x^{(j)}$ 是一个数值，就是两个输入特征向量的内积。预测函数为：

$w^{T}x+b=\sum _{i=1}^{m}\alpha _{i}y^{(i)}x^{(i)T}x+b$

当 $w^{T}x+b\geqslant 0$ ，预测函数为类别1，当 $w^{T}x+b<0$ ，预测类别为-1。注意到预测函数里也包含式子 $x^{(i)T}x$ 。 $x^{(i)T}x^{(j)}$ 是两个向量内积，它的物理含义是衡量两个向量的相似性。典型地，当两个向量相互垂直是，即完全线性无关，此时 $x^{(i)T}x^{(j)}=0$ 。引入核函数后预测函数为：

$w^{T}x+b=\sum _{i=1}^{m}\alpha _{i}y^{(i)}K(x^{(i)},x)+b$

如图：

解决这个问题的方式是：用一定规则把这些无法进行线性分割的样本映射到更高纬度的空间里，然后找出超平面。

SVM的核函数就是为了实现这种相似性映射。最简单的核函数是 $K(x^{(i)},x^{(j)})=x^{(i)T}x^{(j)}$ ，它衡量的是两个输入特征向量的相似性。可以通过定义和函数 $K(x^{(i)},x^{(j)})$ 来重新定义相似性，从而得到想要的映射。例如在基因测试领域，我们需要根据DNA分子的特征来定义相似性函数，即核函数。在文本处理领域，也可以自己定义和函数来衡量两个词之间的相似性。

上述参考博客：SVM支持向量机原理及核函数

其详细的原理及推导，可参考博客：Svm算法原理及实现

4、利用SVM模型进行文本分类

以cnews.test.txt文本为例，基本处理部分与朴素贝叶斯分类部分类同，不同的demo如下：

from sklearn import svm
count_vector = CountVectorizer()
# 该类会将文本中的词语转换为词频矩阵，矩阵元素a[i][j]表示j词在i类文本下的词频
vector_matrix = count_vector.fit_transform(train_X)

# tfidf度量模型
train_tfidf = TfidfTransformer(use_idf=False).fit_transform(vector_matrix)
# 将词频矩阵转化为权重矩阵，每一个特征值就是一个单词的TF-IDF值

# SVM分类
clf = svm.LinearSVC(C=1.6, class_weight=None,dual=True, fit_intercept=True,intercept_scaling=1, loss='squared_hinge',
                        max_iter=2500,multi_class='ovr', penalty='l2', random_state=None,tol=0.0001,verbose=0)
clf.fit(train_tfidf,train_y)

# SVM分类测试
test_vector = count_vector.transform(test_X)
test_tfidf = TfidfTransformer(use_idf=False).fit_transform(test_vector)
predict_result = clf.predict(test_tfidf)
print('SVM分类效果：%f'%accuracy_(test_y,predict_result))

# 结果：SVM分类效果：0.986000

全部代码见：链接

5、PLSA、共轭先验分布

1）PLSA(基于概率统计的隐性语义分析)

PLSA(Probabilistic Latent Semantic Analysis，基于概率统计的隐性语义分析)。在介绍PLSA之前，先介绍LSA(隐性语义分析)。LSA的目的是要从文本中发现隐含的语义维度，即"Topic"或"Concept"。在文档的空间向量模型(VSM)中，文档被表示成由特征词出现概率组成的多维向量，这种方法的好处是可以将query和文档转化为同一空间下的向量计算相似度，可以对不同词项赋予不同的权重，在文本检索、分类、聚类问题中都得到了广泛的应用。然而，向量空间模型没有能力处理一词多义和一义多词问题，例如同义词也分别被表示成独立的一维，计算项链的宇轩相似度时会低估用户期望的相似度，而某个词项有多个词义时，始终对应同一维度，因此计算的结果会高估用户期望的相似度。

LSA方法的引入可以减轻类似的问题。LSA的核心思想是将词和文档映射到潜在语义空间，再比较其相似度。基于SVD分解，我们可以构造一个原始向量矩阵的一个低秩逼近矩阵，具体的做法是将词项文档矩阵做SVD分解。如图：

引用吴军老师在 “矩阵计算与文本处理中的分类问题” 中的总结：

三个矩阵有非常清楚的物理含义。第一个矩阵 U 中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵 V 中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵 D 则表示类词和文章类之间的相关性。因此，我们只要对关联矩阵 X 进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。

举例：如图：

在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说 stock 和 market 可以放在一类，因为他们老是出现在一起，real 和 estate 可以放在一类，dads，guide 这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。

尽管基于SVD的LSA取得了一定的成功，但其缺乏严谨的数理统计基础，而且SVD分解十分耗时。Hofmann在SIGIR'99上提出了基于概率统计的PLSA模型，并且用EM算法学习模型参数。PLSA的概率图模型如下：

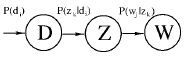
其中D代表文档，Z代表隐含类别或者主题，W为观察到的单词， $P(d_{i})$ 表示单词出现在文档 $d_{i}$ 的概率， $P(z_{k}|d_{i})$ 表示文档 $d_{i}$ 中出现主题 $z_{k}$ 下的单词概率， $P(w_{j}|z_{k})$ 给定主题 $z_{k}$ 出现单词 $w_{j}$ 的概率。并且每个主题在所有词项上服从Multinomial分布，每个文档在所有主题上服从Multinomial分布。整个文档的生成过程是这样的：

(1) 以 $P(d_{i})$ 的概率选中文档 $d_{i}$ ；(2)以 $P(z_{k}|d_{i})$ 的概率选择主题 $z_{k}$ ；(3) 以 $P(w_{j}|z_{k})$ 的概率产生一个单词 $w_{j}$ 。

我们可以观察到的数据就是 $(d_{i},w_{j})$ 对，而 $z_{k}$ 是隐含变量。 $(d_{i},w_{j})$ 的联合分布为：

$P(d_{i},w_{j})=P(d_{i})P(w_{j}|d_{i}),P(w_{j}|d_{i})=\sum_{k=1}^{K}P(w_{j}|z_{k})P(z_{k}|d_{i})$

而 $P(z_{k}|d_{i})$ 和 $P(w_{j}|z_{k})$ 分布对应了两组Multinomial分布，我们需要估计这组分布的参数。一般会采用EM算法进行参数估计。

2）共轭先验分布

在共轭先验分布(Conjugate prior distribution)之前，先复习贝叶斯公式：

$P(Y_{i}|X)=\frac{P(X|Y_{i})P(Y_{i})}{\sum _{j=1}^{inf}P(X|Y_{j})P(Y_{j})}$

其中 $Y_{1},Y_{2},...$ 是对样本空间的划分。

先验分布：在抽取样本X之前，需要对样本类别Y有所了解的信息，通常称为先验信息.对于样本类别Y的分布称为先验分布，这里是 $P(Y_{i})$ ;

后验分布：在抽取样本X，得到样本信息的情况下关于样本类别Y的概率分布称为后验信息，这里是 $P(Y_{i}|X)$ ;

共轭先验分布：在贝叶斯概率理论中，如果后验概率 $P(Y_{i}|X)$ 和先验概率 $P(Y_{i})$ 满足同样的分布律(形式相同，参数不同)。那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

常见的共轭先验分布如图：

6、LDA主题模型原理

LDA主题模型原理在博客："关键词抽取模型"中已经提及，不做重复赘述。

博客：“主题模型 LDA 入门（附 Python 代码）”讲解比较清楚。

7、使用LDA生成主题特征，进行文本分类

LDA(Latent Dirichlet Allocation)是一种文档主题生成模型，也称一个三层贝叶斯概率模型，包含词、主题和文档三层结构。所谓生成模型，就是说，我们认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布。

LDA是一种非监督机器学习技术，可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏主题信息。它采用了词袋(bag of words)的方法，这种方法将每篇文档视为一个词频向量，从而将文本信息转化为易于建模的数字信息。但是此代方法没有考虑词与词之间顺序，这简化了问题的复杂性，同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。

此处以cnews.test.txt文档为例，介绍LDA生成主题特征，进行文本分类的过程，demo如下(可见本节所有代码:戳链接)：

from nltk.stem.wordnet import WordNetLemmatizer
import gensim
from gensim import corpora

# 数据准备
# preprocess用于将一个文本文档进行切词，并以字符串形式输出切词结果
path = './cnews.test.txt'
with open(path,'r',encoding='UTF-8') as f:
    cnews_test = f.readlines()
# 取test中前3000出来分为2000为训练样本，1000测试样本
cnews_test = cnews_test[500:1000]+cnews_test[1500:2000]+cnews_test[2500:3000]+cnews_test[3500:4000]
# 将test中的label取出
test_label,test_x = [],[]
n = list(range(len(cnews_test)))
random.shuffle(n)
for i in n:
    each = cnews_test[i]
    each0 = each.split('\t')
    test_label.append(each0[0])
    test_x.append(each0[1])
    
# 载入停用词字典，对其进行去停用词
with open('./stopword.txt','r',encoding='UTF-8') as f:
    stopwords = f.readlines()
a = ''
for each in stopwords:
    a = a + ' '+each
stopwords = a.replace('\n','').split(' ')
stopwords = [each for each in stopwords if each not in ['\n','']]

test_x = [[each0 for each0 in jieba.cut(each) if each0 not in stopwords] for each in test_x] 

# 创建语料的词语词典，每个单独的词语都会被赋予一个索引
dictionary = corpora.Dictionary(test_x)
# 使用上面的词典，将转换文档列表（语料）变成 DT 矩阵
doc_term_matrix = [dictionary.doc2bow(doc) for doc in test_x]

#  使用 gensim 来创建 LDA 模型对象
Lda = gensim.models.ldamodel.LdaModel
# 在 DT 矩阵上运行和训练 LDA 模型
ldamodel = Lda(doc_term_matrix,num_topics=2,id2word=dictionary, passes=50)
# 输出结果
result_lda = ldamodel.print_topics(num_topics=2,num_words=20)
print(result_lda)

（文本分类那一块之后再琢磨琢磨。。。。）

参考资料：

链接1：朴素贝叶斯算法原理小结

链接2：浅谈朴素贝叶斯算法原理

链接3：sklearn：朴素贝叶斯（naïve beyes）

链接4：使用朴素贝叶斯进行中文文本分类

链接5：Svm算法原理及实现

链接6：SVM原理篇之手撕SVM

链接7：SVM支持向量机原理及核函数

链接8：PLSA及EM算法

链接9：LSA，pLSA原理及其代码实现

链接10：概率语言模型及其变形系列(1)-PLSA及EM算法

链接11：先验分布、后验分布、共轭分布、共轭先验分布

链接12：主题模型 LDA 入门（附 Python 代码）

士416

关注

2
点赞
踩
10

收藏

觉得还不错? 一键收藏
1
评论
NLP学习__task4：传统机器学习：朴素贝叶斯、SVM、PLSA、LDA

1、朴素贝叶斯的原理在所有机器学习分类算法中，朴素贝叶斯和其他绝大多数分类算法不同。不同于：例如决策树、KNN、逻辑回归、支持向量机等，这些都是判别方法，即直接学习出特征输出Y和特征X之间的关系，也是决策数；而朴素贝叶斯是生成方法，即直接找出特征输出Y和特征X的联合分布，然后用得出。1）朴素贝叶斯的定理首先，明确贝叶斯统计方式与统计学中的频率概念不同：从频...
复制链接

扫一扫