fvdm 跟驰模型 matlab仿真_MATLAB——信号灯控制下T字型路口双车道交通仿真模型...

T字型路口因为其特殊形状是交通事故多发的地段，本模型旨在建立有信号灯控制的情况下T字型路口双车道交通流模型，是用MATLAB写的元胞自动机模型。

这是仿真模型输出效果

这个模型原理其实很简单，概括的说，就是每个时间步内确定完每一个元胞的状态（包括车辆的位置信息和速度信息），然后完成位置更新。

因为没有加入车道换道功能，所以代码实现的难度其实是在T字型路口换道和直行情况的全部考虑。

简单介绍一下T字型路口的交通情况。有信号灯控制的T字型路口的交通情况有两种状态，一个状态是横向车道允许直行，禁止左转，另一个状态是横向车道直行停止，可以左转，而右转始终可以，只要做到避让即可。

下面是对T字型路口的模型

T字型路口模型

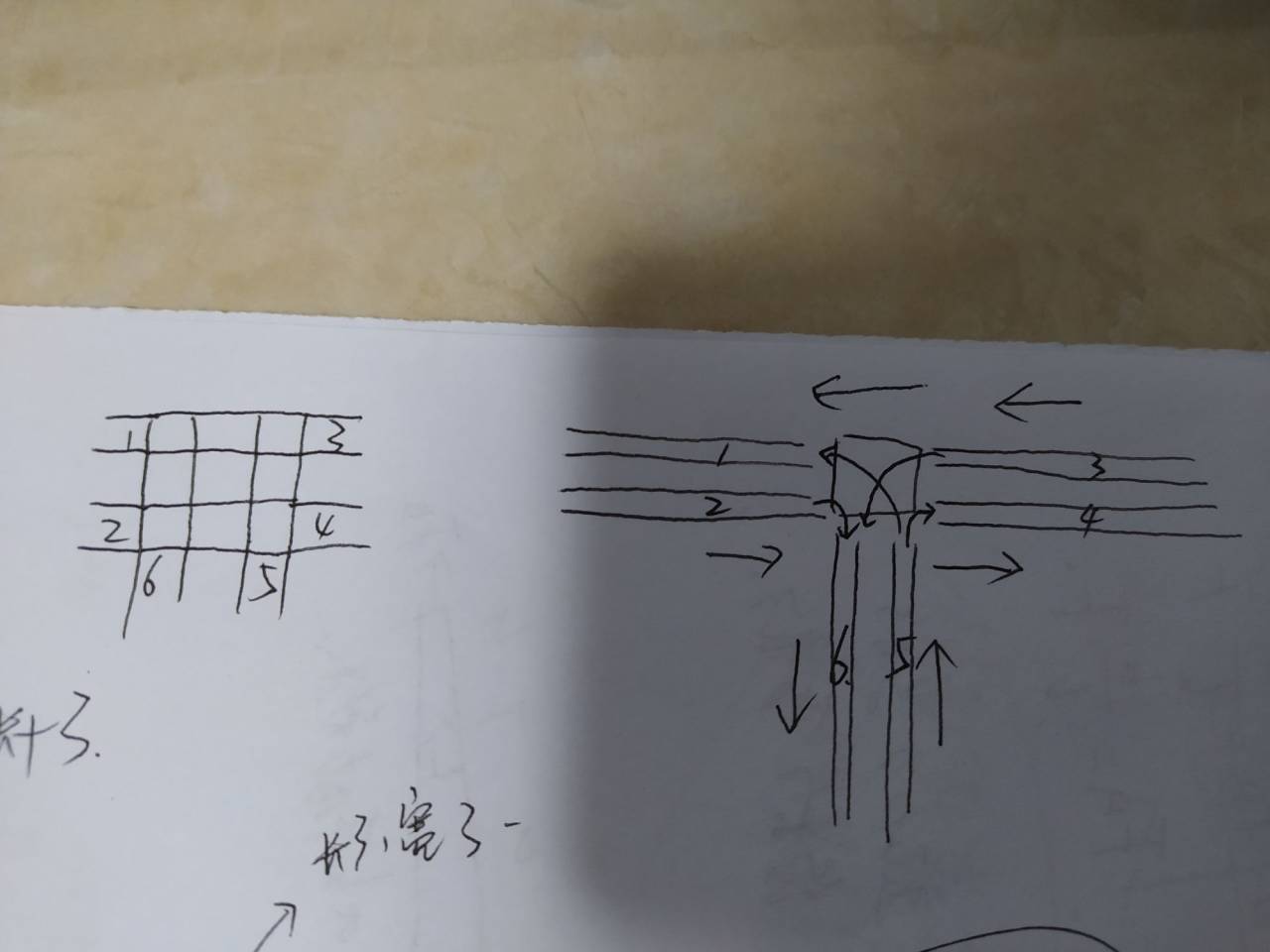
主要思路就是将T字型路口分为两大部分，一是由六个车道组成的车道部分，二是路口（即中间方块），将六个车道的信息储存在（6，way_length/2）的矩阵中（所以横向车道是纵向车道长度的两倍，而定义横向车道长度为输入的车道长度），而将路口的信息储存在（3,3）的矩阵中。

其中，way_length是车道长度。

而车辆状态则采取元胞自动机的思想，一辆车有两个信息，位置信息和速度信息，位置信息储存在元胞矩阵中，而速度信息则受上一时间步该车辆前进方向两个元胞上有无车辆决定，但路口内车辆速度信息还有别的规则，在此不赘述。

值得注意的是：各车道非尾车（前进方向最后一辆）运行状态不受信号灯影响，2,3,5车道尾车运动状态受到红绿灯运动影响，而1,4,6车道则不受。

因此，在确定一个时间步元胞状态时，2,3,5车道尾车及路口内车辆状态就要因为信号灯而分两种状态考虑，再加上2,3,5车道尾车的换道行为，让路口内情况变得复杂，所以我写了一百多行的if语句。

整体思路就是这样，细节代码中都有，所以我先贴代码，最后再说说模型先存在哪些问题。

脚本：

%%  车流密度不变下的双向两车道仿真（T 字形路口）
%    输出参数： v_average——平均速度
%               change_lane_times——换道次数（1000 次）
%               density——车流密度
%%  参数设置 
way_length = 40;        %车道长度（偶数）
time_span = 0.1;        %仿真步长时间
MaxTime = 500;          %仿真步长数目
fp = 5;                 %车道入口处新进入车辆的概率（列向量）
pro_right_5_3=0.5;      %交叉口处车辆行为的概率向量(5 车道右转,3车道右转）
pro_right_2=0.5;        %路口处2车道右转的概率
%% 调用函数 
[ v_average, change_lane_times, density ] = CA_T_model ( way_length,time_span,fp,MaxTime,pro_right_5_3,pro_right_2);
%%  输出参数
disp('平均速度为：')
disp( v_average)
disp('换道次数为：')
disp(change_lane_times)
disp('交通流密度为')
disp(density)

函数：

%%   本函数为在某一特定车流密度下的（车流密度由 fp 决定）双向两车道仿真模型
%%   注意：
      %由红绿灯控制两个状态，一是可以横向车道直行，二是横向车道直行停止，可以左转，右转始终可以做到避让即可
      %每个车辆都有两个信息，一是位置信息（用way储存），而是速度信息（用v储存），其中速度包括慢车，快车，停车，分别用1,2,3表示
      %为了储存方便，横向车道（不包括路口方块方块）为纵向车道长度的两倍，而将横向车道长度定义为车道长度
      %此模型中信号灯只有红灯和绿灯，红灯时长可以通过参数time_red_light来调节
      %转弯路径说明：5车道左转通过（3,2），（2,1），（1，1）到达way（1,1）；右转则通过（3,3）到达way（4,1）
      %所有车辆进入路口速度最大为1
%%   参数说明：
      % 换道次数:change_lane_times
      % 平均速度;v_average
      % 平均密度;density
      % way_number:车道数目
      % way_length:车道长度
      % v_average:平均速度
      % density:车流密度
      % MaxTime:仿真步长数目
      % time_span：输出图片变换间隔时间
      % fp:车道入口处新进入车辆的概率列向量（2,3,5 车道）
      % pro_left:路口处车辆行为的概率向量(5 车道右转,3车道右转）
      % pro_right:路口处2车道右转的概率
function [ v_average, change_lane_times, density ] = CA_T_model( way_length,time_span,fp,MaxTime,pro_right_5_3,pro_right_2)
%%  初始化换道次数
change_lane_times=0;
%%  双车道
wa