本文详细介绍了如何使用差分TDR（DTDR）测量和分析差分对的各种特性，包括差分阻抗、耦合度、双绞线电缆的特性以及模式转换。通过实例展示了测量过程和影响信号完整性的因素，强调了差分信号在穿越间隙、转换为共模信号时的行为，为高速串行链路设计提供了关键洞察。
概述
前文中我们探讨了两条单端带耦合的传输线。每条线都有其自身的阻抗曲线和时延属性， 每条线上都有另一条线上的信号造成的近端和远端噪声。这是对两条不同的线进行描述的一种方法。
是德科技：信号完整性分析系列- 第 1 部分：单端口 TDRzhuanlan.zhihu.com
另一个方法是将这同样的两条线作为单个差分对进行描述。两种类型的信号可以在差分对上传播：差分信号和共模信号。在差分信号中，一条线上的电压是另一条线的负值。差分对上的差分信号分量是两条线之间的电压差。这意味着在差分信号中，返回平面上测得的一条线上的电压是另一条线的负值。大多数高速串行链路采用差分信号来发送信息。由于接收机的原因，差分信号比单端信号具有更好的信噪比和抗扰度。
共模信号分量是一个差分对中两个信号的平均值。这意味着共模信号其实是测量一对传输线的共模电压。由于共模信号很少用于携带信息，如果此信号变得过大以至于使得差分接收机饱和，或者超出了外部电缆上的产品，有时会带来一些问题，因为这样的信号会产生电磁干扰（EMI）。
当差分信号在互连上传播时，它会驱动差分对的奇模，差分信号会看到互连的差分阻抗。当共模信号在互连上传播时，它会驱动差分对的偶模，共模信号会看到差分对的共模阻抗。
如需表征差分对，TDR 必须驱动差分信号或共模信号二者之一，并将反射的差分信号或共模信号作为响应进行测量。这需要将两个通道连接到差分对的同一端，且具有等同的两个同步激励，即向被测件发射差分信号或发射共模信号。这可以通过差分 TDR（DTDR） 实现。
如图 49 所示，设置为差分激励时，两个通道的激励完全相反；而设置为共模激励时， 输出电压完全相同。
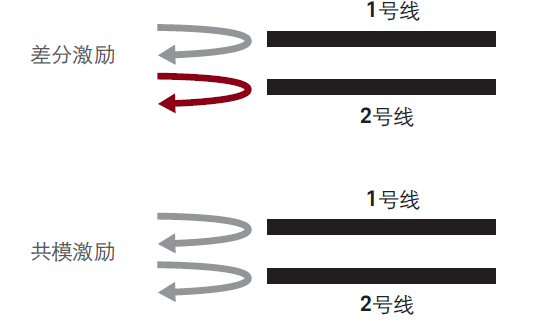
图 49. 表征查分对的配置。
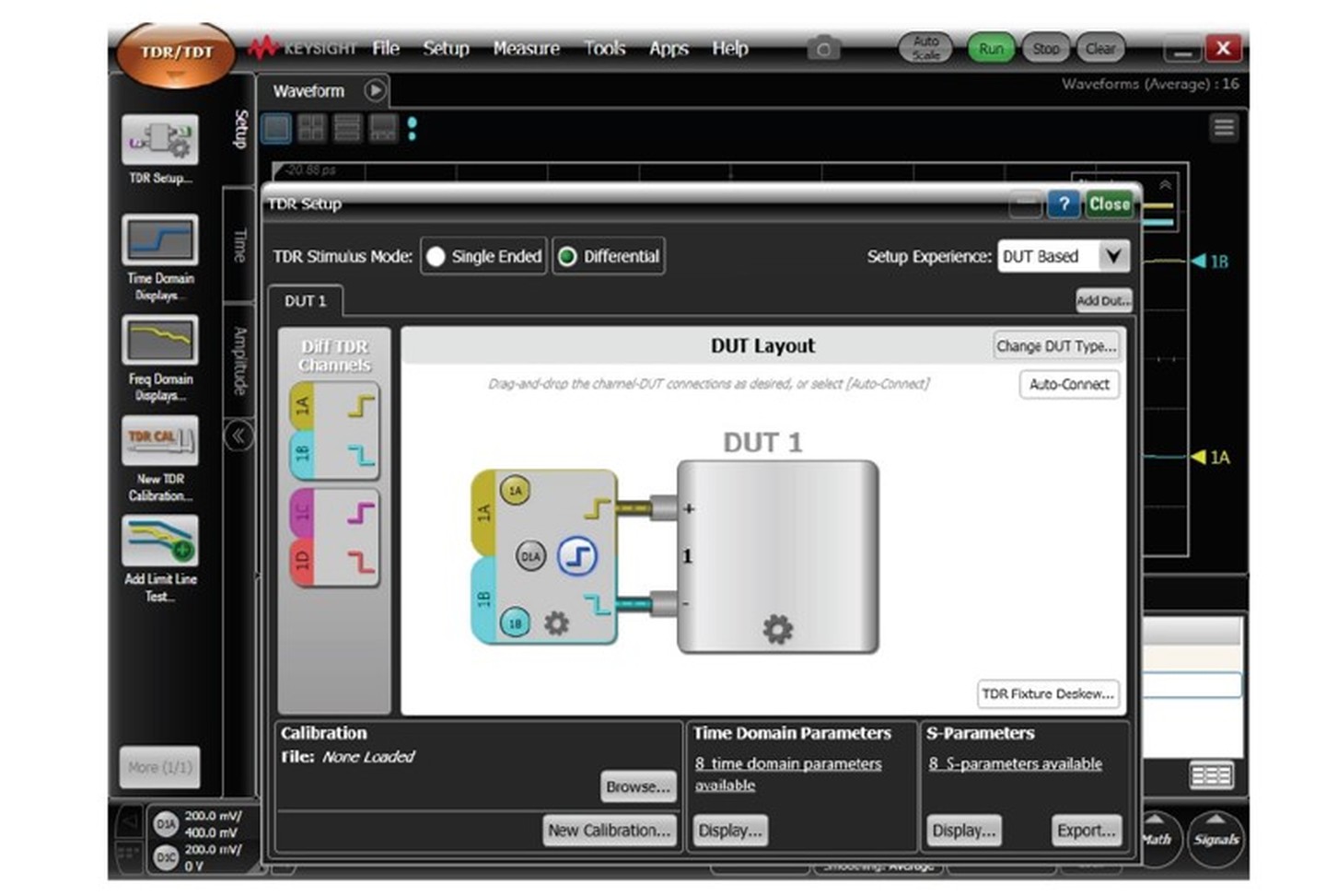
在应用中，为 DTDR 设置一种操作模式。如需将 DTDR 调整为差分激励操作模式，可点击 TDR 设置打开 TDR 设置窗口，然后在 TDR 激励模式中选择差分。
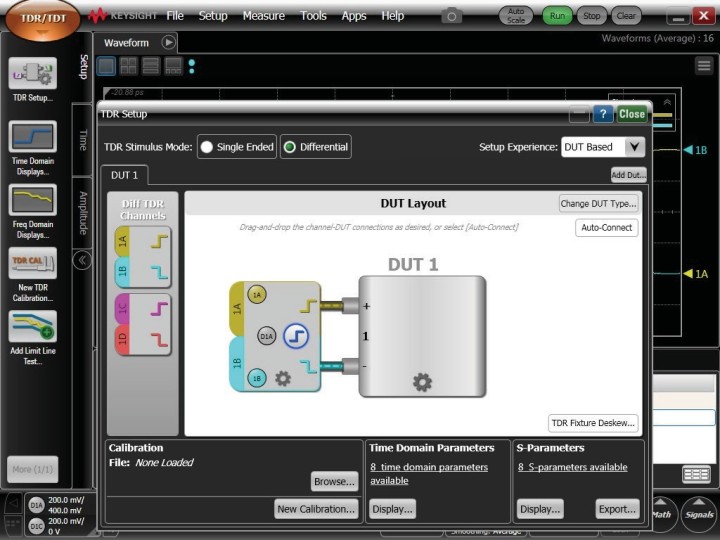
图 50. 用于差分测量的 DTDR 设置屏幕。
图 50 所示为调整差分操作模式的设置屏幕。请注意，不要将共模操作模式与能驱动差分对的偶模混淆。屏幕标签上带有共模的“模式”指的是“操作模式”，而不是驱动差分对的模式。
4.2 分别测量与每个差分对相关联的五个阻抗
如果单端传输线是差分对的一部分，那么它确实有三个不同的特性阻抗。这三个阻抗分别是单端阻抗，即当差分对中另一条线上存在恒定电压时的瞬时阻抗；奇模阻抗，即当差分对以奇模方式驱动时线上的瞬时阻抗和
最低0.47元/天 解锁文章
扫一扫
7665
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
