半圆阴影_此题求阴影部分面积，很多学生不知如何思考，别忘了用计算来推理...

今天，数学世界为大家讲解一道初中数学几何题，此题并不难，但不能只是观察图形，必须通过计算来进行推理。请大家先思考一下，再看后面的解答过程！有些人可能认为这道题很简单，但是学生要学习的就是解题思路和思考的过程！

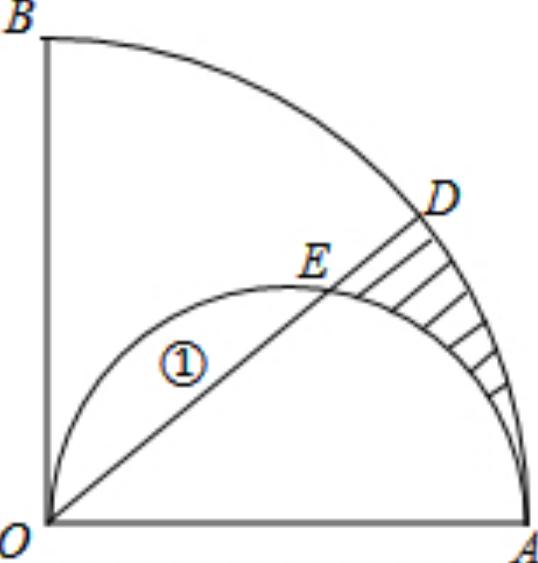
例题：(初中数学几何题)如图，已知∠BOA=90°，∠AOD=45°，以AO为半径画扇形ABO交OD于D，以AO为直径画半圆交OD于E，若图中①的面积为1平方厘米，求阴影部分的面积是多少平方厘米？

对于此题，很多学生不知道怎么思考，而家长直接表示初中数学都已经忘记了，实在不会做。实际上，这道题并没有多大难度，但只有通过计算来进行推理，才能完成此题，解决此题的关键是灵活运用扇形的面积公式。下面，我们就一起来分析这道例题吧！

解析：设OA=2r，(因为题中没有任何线段长度，所以通常设半径或直径，为了便于计算，可设直径AO=2r)

∵∠BOA=90°，

∴S扇形AOB=1/4·π(2r)^2=πr^2，

∵∠AOD=45°=∠BOD，(因为∠BOA=90°，∠AOD=45°，所以∠BOD=45°)

∴S扇形AOD=S扇形BOD=1/2S扇形AOB=1/2πr^2，

(半径相同且圆心角相等的扇形面积相等)

∵S半圆=1/2πr^2，

∴S扇形AOD=S半圆，(通过计算面积得出两部分的面积相等)

∴S阴影=S图①，(两图减去公共的空白部分)

即S阴影=1平方厘米。

答：阴影部分的面积是1平方厘米。

温馨提示：由于文章是原创作者猫哥一字一句打出来的，所以文中可能会出现一些不影响阅读的错误，还请大家谅解！若朋友们还有不明白的地方或者有更好的解题方法，欢迎留言参与讨论。