本质矩阵svd分解_使用numpy解PCA, SVD

1.概述

主成分分析（PCA：principal component analysis）和奇异值分解(SVD：singular value decomposition)之间到底有何关联，以及如何使用numpy实现。

主成分分析和奇异值分解是探索性数据分析（EDA）和机器学习中常用的降维方法。它们都是经典的线性降维方法，它们试图在原始高维数据矩阵中找到特征的线性组合以构造有意义的数据集表示形式。在降低尺寸方面，它们是不同领域的首选：生物学家经常使用PCA来分析和可视化来自种群遗传学，转录组学，蛋白质组学和微生物组的数据集中的来源差异。同时，SVD，特别是其简化版本的截断SVD，在自然语言处理领域中更为流行，以实现巨大而稀疏的词频矩阵的表示。 人们可能会发现，PCA和SVD的结果表示在某些数据中是相似的。实际上，PCA和SVD是密切相关的。在本文中，我将使用一些线性代数和几行numpy代码来说明它们之间的关系。

2.协方差矩阵

协方差可量化两个随机变量X和Y之间的联合变量，其计算公式如下：

来自数据矩阵X的特征的成对协方差的方阵（n个样本×m个特征）。从协方差的定义中可以观察到，如果两个随机变量均以0为中心，则随机变量的期望值将变为0，并且可以将协方差计算为两个特征向量x和y的点积。因此，以所有特征为中心的数据矩阵的协方差矩阵可以计算为：

C =

3.PCA

PCA的目的是找到线性不相关的正交轴，这些正交轴也称为m维空间中的主成分（PC），以将数据点投影到这些PC上。第一台PC捕获数据中最大的差异。让我们通过将PCA拟合到2D数据矩阵上来直观地了解PCA，该矩阵可以方便地用2D散点图表示：

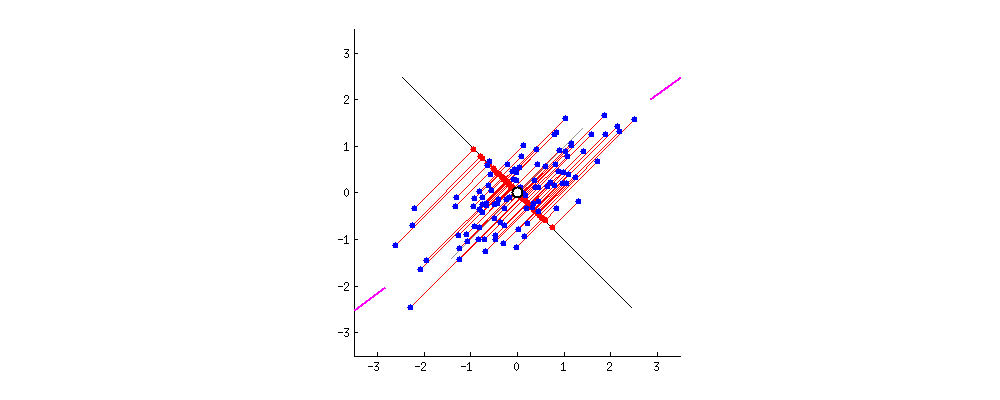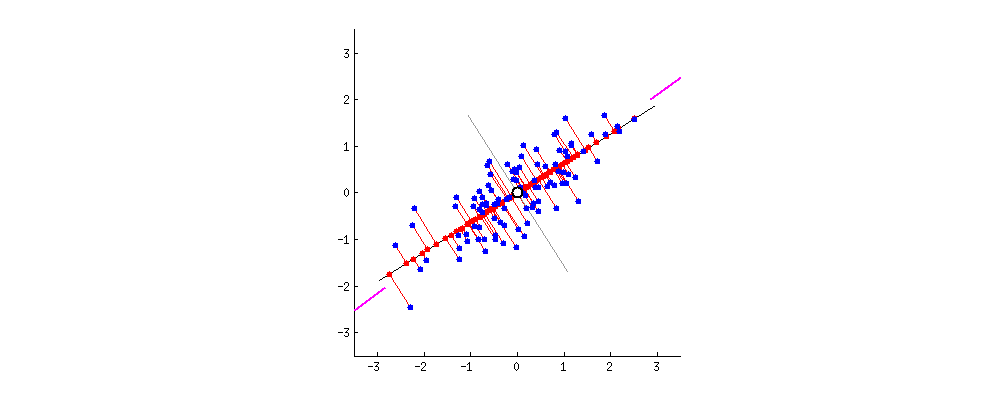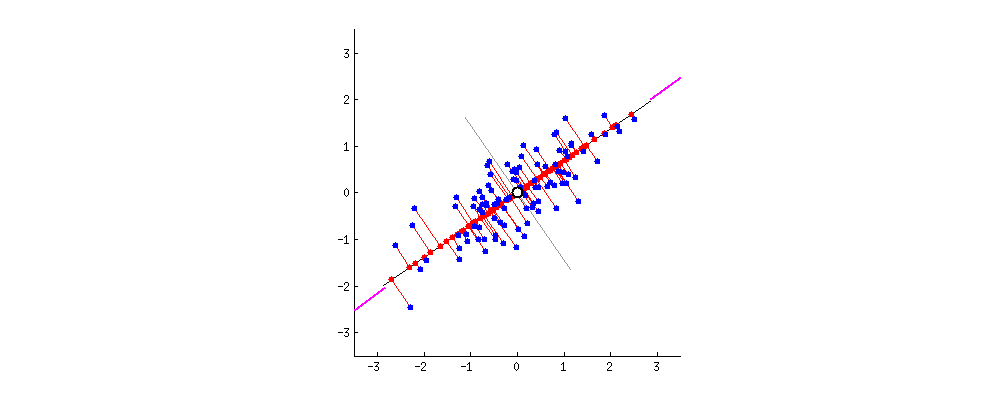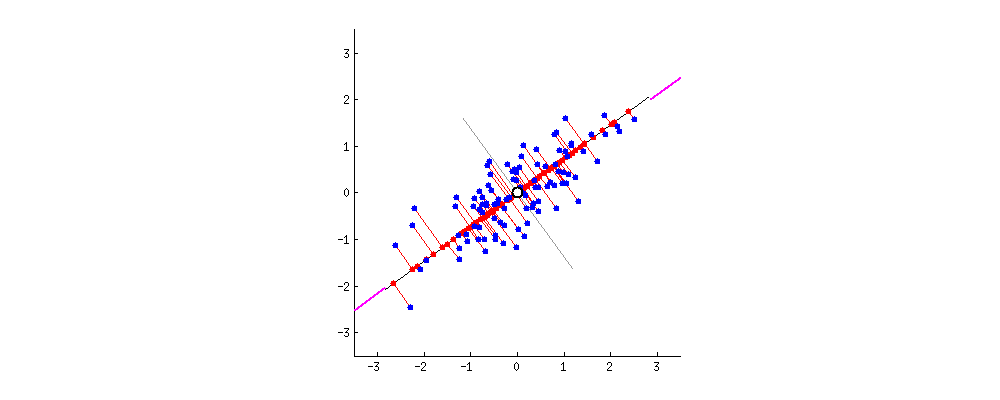
由于所有PC彼此正交，因此我们可以在二维空间中使用一对垂直线作为两台PC。为了使第一台PC捕获最大的方差，我们旋转我们的PC对以使其其中的一个与数据点的分布最佳对齐。接下来，所有数据点都可以投影到PC上，它们的投影（PC1上的红色点）本质上是数据集降维的结果。中提琴，我们只是将矩阵从2-D缩减为1-D，同时保留了最大的方差！

可以通过协方差矩阵C的特征分解来确定PC。毕竟，特征分解的几何意义是通过旋转找到C的特征向量的新坐标系。

假设C的特征向量组成的矩阵为W, 特征值组成的对角矩阵为

，则有如下公司成立：

......................................................(1)

在上式中，协方差矩阵C（m×m）被分解为特征向量W（m×m）的矩阵和m个特征值Λ的对角矩阵。特征向量是W中的列向量，实际上是我们要寻找的PC。然后，我们可以使用矩阵乘法将数据投影到PC空间上。出于降维的目的，我们可以将数据点投影到前k个PC上，作为数据的表示形式：

可以使用numpy轻松实现PCA，因为已经完成了执行本征分解的关键功能（np.linalg.eig）：

def pca(X):
  # Data matrix X, assumes 0-centered
  n, m = X.shape
  assert np.allclose(X.mean(axis=0), np.zeros(m))   #确保X已经中心化，每个维度的均值为0
  # Compute covariance matrix
  C = np.dot(X.T, X) / (n-1)
  # Eigen decomposition
  eigen_vals, eigen_vecs = np.linalg.eig(C)
  # Project X onto PC space
  X_pca = np.dot(X, eigen_vecs)
  return X_pca

4.SVD

SVD是用于实矩阵和复矩阵的另一种分解方法。它将矩阵分解为两个unit矩阵（U，V *）和奇异值（Σ）的矩形对角矩阵的乘积：

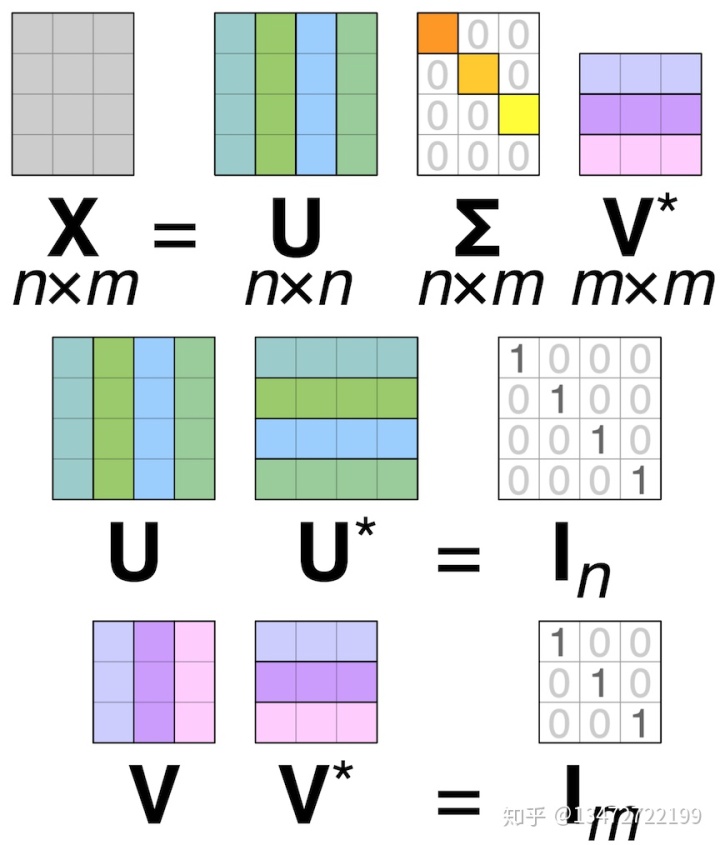
在大多数情况下，我们使用实数矩阵X，并且所得的unit矩阵U和V也将是实数矩阵。因此，U的共轭转置就是正则转置。

SVD也已经在numpy中实现为np.linalg.svd。要使用SVD转换数据，请执行以下操作：

def svd(X):
  # Data matrix X, X doesn't need to be 0-centered
  n, m = X.shape
  # Compute full SVD
  U, Sigma, Vh = np.linalg.svd(X, 
      full_matrices=False, # It's not necessary to compute the full matrix of U or V
      compute_uv=True)
  # Transform X with SVD components
  X_svd = np.dot(U, np.diag(Sigma))
  return X_svd

5.SVD与PCA的关系

PCA和SVD是紧密相关的方法，都可以应用于分解任何矩形矩阵。我们可以通过在协方差矩阵C上执行SVD来研究它们的关系：

.............................................(2)

而PCA的C的公式为：

从上面的推导中，我们注意到结果与C的特征分解具有相同的形式，我们可以很容易地看到奇异值（Σ）和特征值（Λ）之间的关系：

用numpy确认：

# Compute covariance matrix
C = np.dot(X.T, X) / (n-1)
# Eigen decomposition
eigen_vals, eigen_vecs = np.linalg.eig(C)
# SVD
U, Sigma, Vh = np.linalg.svd(X, 
    full_matrices=False, 
    compute_uv=True)
# Relationship between singular values and eigen values:
print(np.allclose(np.square(Sigma) / (n - 1), eigen_vals)) # True

那么，这意味着什么呢？这表明我们实际上可以使用SVD执行PCA，反之亦然。实际上，大多数PCA实现实际上都是在幕后执行SVD，而不是对协方差矩阵进行特征分解，因为SVD可以更有效地处理稀疏矩阵。此外，SVD的形式有所减少，因此计算起来更加经济。

参考文献：

https://towardsdatascience.com/pca-and-svd-explained-with-numpy-5d13b0d2a4d8​towardsdatascience.com The Web's Most Extensive Mathematics Resource​mathworld.wolfram.com