抛物线中四边形面积最大值_二次函数中常用的求面积法

   求三角形的面积是几何题中常见问题之一，可用的方法也比较多，比如面积公式、割补、等积变形、三角函数甚至海伦公式，下面我们看看在二次函数问题中常用的一种求面积的方法——铅垂法．

问题 

     在平面直角坐标系中，已知A(1,1)、B(7,3)、C(4,7)，求△ABC的面积．

【分析】显然对于这样一个位置的三角形，面积公式并不太好用，割补倒是可以一试，比如这样： 构造矩形ADEF，用矩形面积减去三个三角形面积即可得△ABC面积．这是在“补”， 同样可以采用“割”： 此处AE+AF即为A、B两点之间的水平距离． 由题意得：AE+BF=6． 下求CD： 根据A、B两点坐标求得直线AB解析式为： 由点C坐标(4,7)可得D点横坐标为4， 将4代入直线AB解析式得D点纵坐标为2， 故D点坐标为(4,2)，CD=5, 方法总结 作以下定义： (1)水平宽：A、B两点之间的水平距离； (2)铅垂高：过点C作x轴的垂线与AB交点为D，线段CD即为AB边的“铅垂高”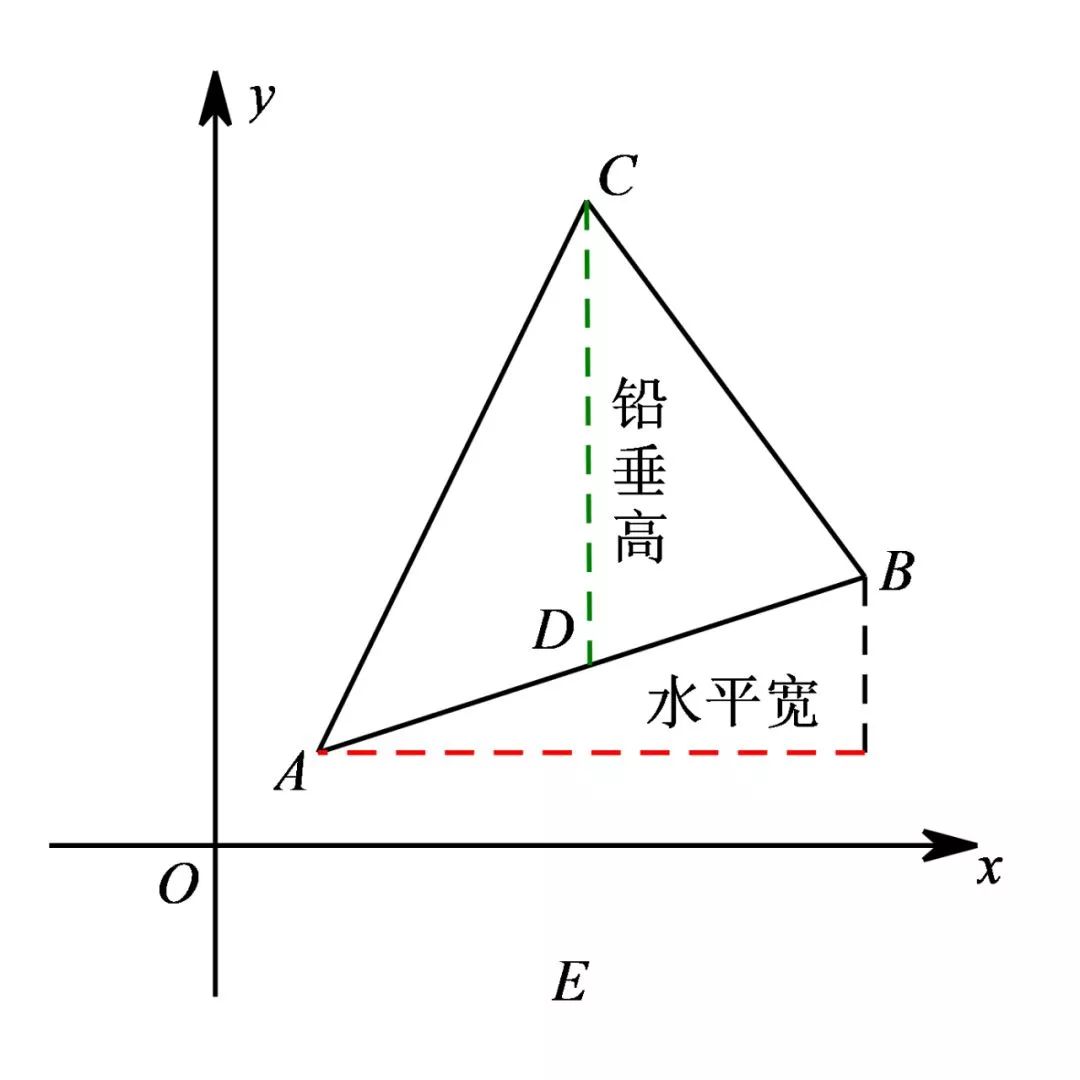． 如图可得： 【解题步骤】 (1)求A、B两点水平距离，即水平宽； (2)过点C作x轴垂线与AB交于点D，可得点D横坐标同点C； (3)求直线AB解析式并代入点D横坐标，得点D纵坐标； (4)根据C、D坐标求得铅垂高； (5)利用公式求得三角形面积．

中考真题

1   如图，已知抛物线y=ax²+bx+5经过A(-5,0)、B(-4,-3)两点，与x轴的另一个交点为C． (1)求该抛物线的表达式； (2)点P为该抛物线上一动点(与点B、C不重合)，设点P的横坐标为t．当点P在直线BC的下方运动时，求△PBC的面积的最大值． 【分析】 (1)y=x²+6x+5； (2)取BC两点之间的水平距离为水平宽，过点P作PQ⊥x轴交直线BC于点Q，则PQ即为铅垂高． 根据A、C两点坐标得AC=4， 根据B、C两点坐标得直线BC解析式：y=x+1， 设P点坐标为(m，m²+6m+5)， 则点Q(m，m+1)， 得PQ=-m²-5m-4， 考虑到水平宽是定值，故铅垂高最大面积就最大． 【小结】选两个定点作水平宽，设另外一个动点坐标来表示铅垂高．     问题      拆解四边形

如何求一个普通的四边形的面积？

解法也很普通，连对角线分割为两个三角形即可求得面积．至于三角形面积则可用铅垂法．

中考真题

1   已知抛物线y=ax²+bx-4经过点A(2,0)、B(-4,0)，与y轴交于点C．

(1)求这条抛物线的解析式；

(2)如图，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；

【分析】

(1)y=0.5x²+x-4；

(2)此处四边形ABPC并非特殊四边形，所以可以考虑连接对角线将四边形拆为两个三角形求面积．

若连接AP，则△ABP和△APC均为动三角形，非最佳选择；

若连接BC，可得定△ABC和动△BPC，只要△BPC面积最大，四边形ABPC的面积便最大．

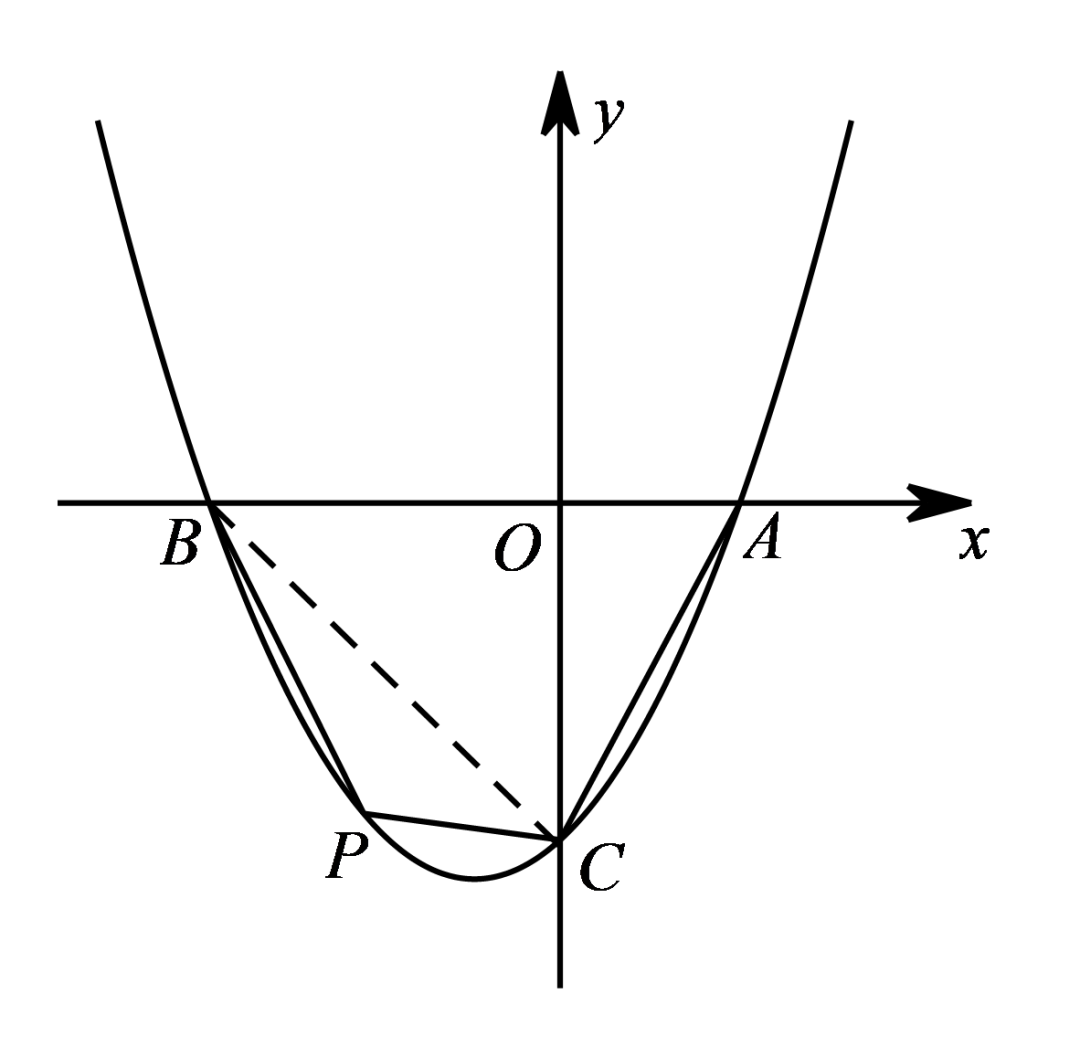
考虑A(2,0)、B(-4,0)、C(0，-4)，

接下来求△BPC的面积，设P点坐标为(m，0.5m²+m-4)，

连接BC，则直线BC的解析式为：y=-x-4

过点P作PQ⊥x轴交BC于点Q，则Q点坐标为(m，-m-4)，

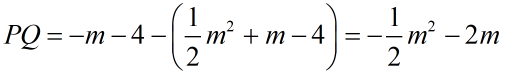
当m=-2时，PQ取到最大值2，此时△BPC面积最大，四边形ABPC面积最大．

此时P点坐标为(-2，-4)．

已知抛物线y=ax²+1.5x+4的对称轴是直线x=3，与x轴相交于A，B两点(点B在点A右侧)，与y轴交于点C．

(1)求抛物线的解析式和A，B两点的坐标；

(2)如图，若点P是抛物线上B、C两点之间的一个动点(不与B、C重合)，是否存在点P，使四边形PBOC的面积最大？若存在，求点P的坐标及四边形PBOC面积的最大值；若不存在，请说明理由；

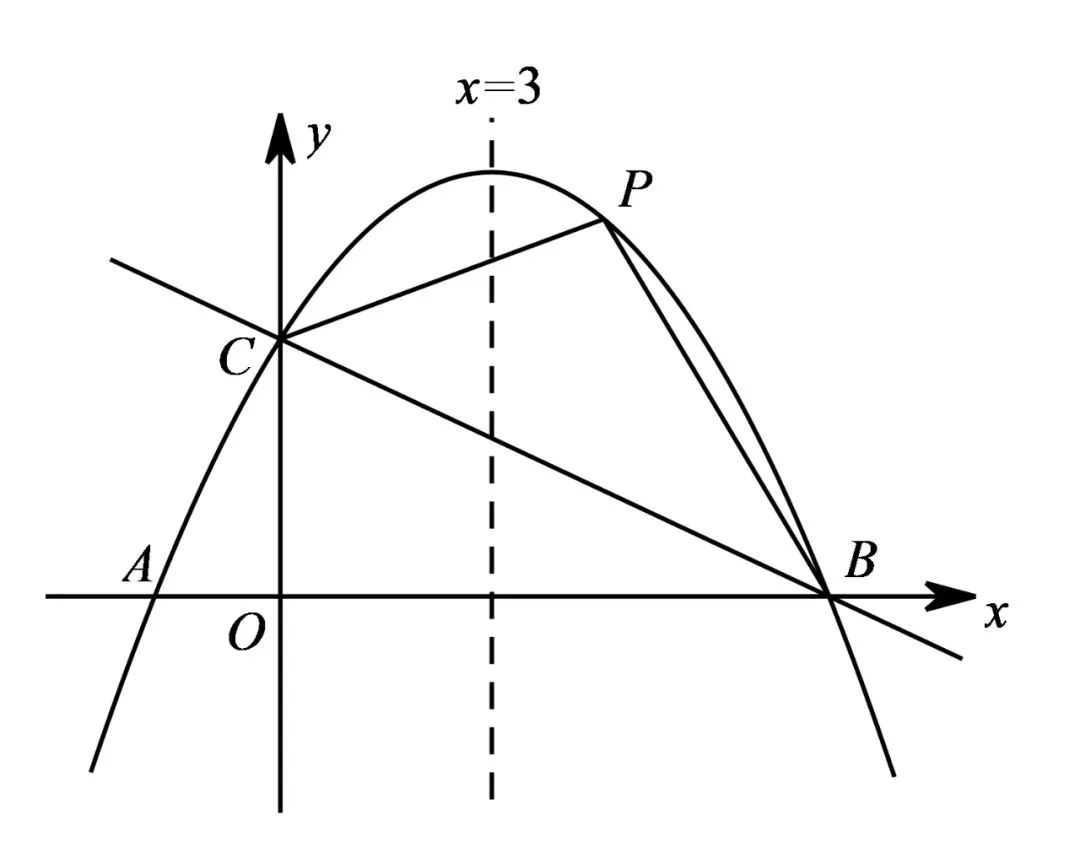
【分析】

(1)抛物线解析式为

点A坐标为(-2,0)，点B坐标为(8,0)．

(2)显然将四边形PBOC拆为△BOC和△PBC，点C坐标为(0,4)，

设P点坐标为

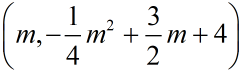
根据B、C坐标可得BC的解析式为y=-0.5x+4

过点P作PQ⊥x轴交BC于点Q，则Q点坐标为(m，-0.5m+4)，

当m=4时，PQ取到最大值4，

故四边形PBOC的最大面积为32，此时P点坐标为(4,6)．

此题四边形已拆好，只要负责计算就可以了，而计算的内容，与三角形无异．

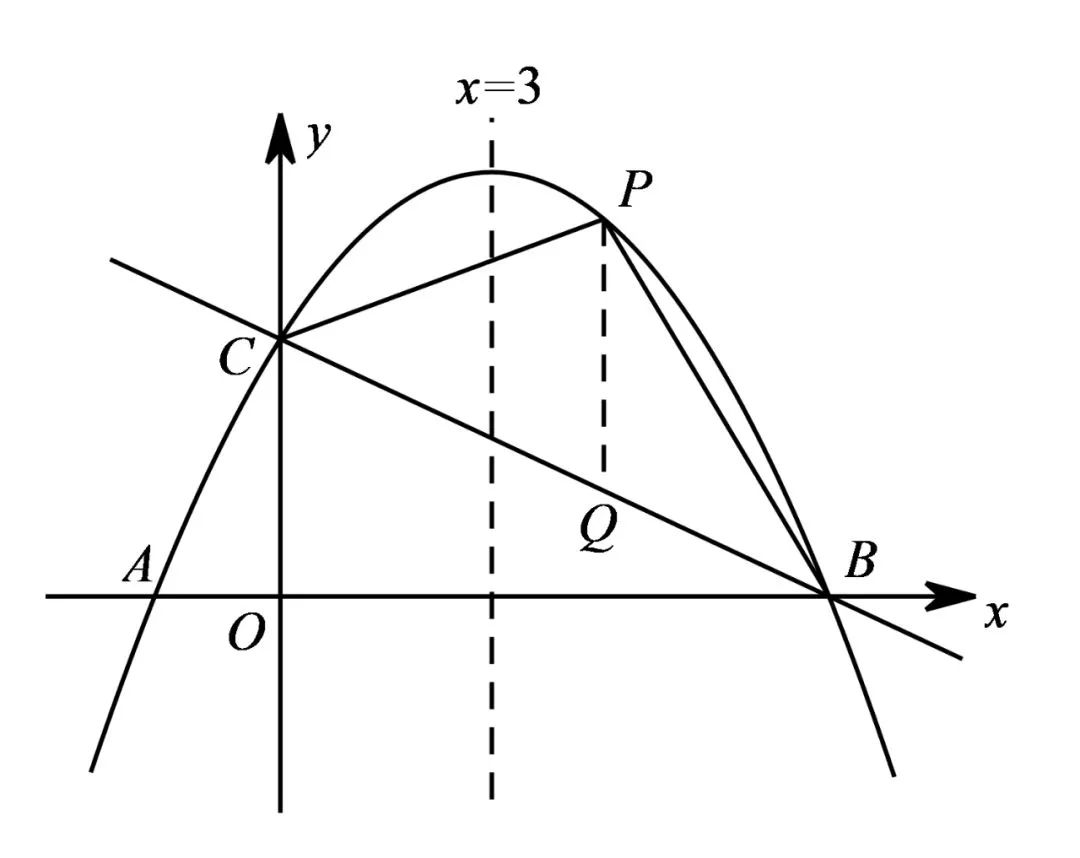
2   如图1，在平面直角坐标系中，直线y=-5x+5与x轴，y轴分别交于A，C两点，抛物线y=x²+bx+c经过A，C两点，与x轴的另一交点为B．

(1)求抛物线解析式及B点坐标；

(2)若点M为x轴下方抛物线上一动点，连接MA、MB、BC，当点M运动到某一位置时，四边形AMBC面积最大，求此时点M的坐标及四边形AMBC的面积；

(3)如图2，若P点是半径为2的圆B上一动点，连接PA、PC，当点P运动到某一位置时，PC+1/2PA的值最小，请求出这个最小值，并说明理由．

【分析】

(1)由题意得：A(1,0)、C(0,5)，代入可解抛物线解析式为：y=x²-6x+5，点B坐标为(5,0)．

(2)显然四边形AMBC可拆为△ABC和△AMB，

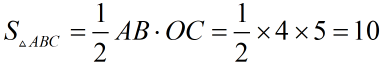
显然，当M点在抛物线顶点时，△AMB面积最大，

此时M点坐标为(3，-4)，

故四边形AMBC面积最大值为10+8=18，此时M点坐标为(3，-4)．

(3)之所以留下这个小问是因为前两个小问也太不够看了，而这个也差不多．

显然是个“阿氏圆”问题，构造1/2PA即可，参考阿氏圆解决方法，

取点D(4,0)，连接PD，任意时刻，均有PD=1/2PA，问题易解．