抛物线中四边形面积最大值_【二次函数与几何综合讲练一】铅垂法求面积最值问题...

专题导入

方法点睛

如图，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”，我们可得出一种计算三角形面积的另一种方法：S△ABC＝1/2ah，即三角形面积等于水平宽与铅垂高乘积的一半．

根据上述方法，我们来得到求三角形的面积的最值问题的方法：S△PAB＝1/2·PQ·|XA-XB|，根据二次函数解析式设出点P的坐标，结合一次函数解析式从而得到点Q的坐标，从而转化为S与点P横坐标之间的二次函数解析式，再根据二次函数增减性求最值.一般情况下，当铅垂线段PQ最大时，S△PAB取得最大值．

典例精讲

类型一：抛物线上动点产生的三角形面积的最值

例1 在平面直角坐标系中，直线y=1/2x-2与x轴交于点B，与y轴交于点C，二次函数y=1/2x2+bx+c的图象经过B，C两点，且与x轴的负半轴交于点A，动点D在直线BC下方的二次函数图象上．

(1)求二次函数的解析式；

(2)如图，连接DC，DB，设△BCD的面积为S，求S的最大值.[来源:学科网ZXXK]

分析

(1)根据题意得到B、C两点的坐标，设抛物线的解析式为y=1/2(x-4)(x-m)，将点C的坐标代入求得m的值即可；(2)过点D作DF⊥x轴，交BC与点F，设D(x，1/2x2-3/2x-2)，则DF=-1/2x2+2x，然后列出S与x的关系式，最后利用配方法求得其最大值即可．

类型二：抛物线上动点产生的四边形的面积

例2. 如图，抛物线y＝ax2＋bx－3与x轴交于点A(1，0)和点B，与y轴交于点C，且其对称轴l为直线x＝－1，点P是抛物线上B，C之间的一个动点(点P不与点B，C重合)．

(1)直接写出抛物线的解析式；

(2)探究:当动点N在对称轴l上时，是否存在PB⊥NB，且PB＝NB的关系，若存在，请求出此时点P的坐标，若不不存，请说明理由；

(3)是否存在点P使得四边形PBAC的面积最大？若存在，请求出四边形PBAC面积的最大值，若不存在，请说明理由．

分析

(1)由对称轴可求得B点坐标，结合A、B两点坐标，利用待定系数法可求得抛物线解析式；(2)过点P作PM⊥x轴于点M，设抛物线对称轴l交x轴于点Q．可证明△BPM≌△NBQ，则可求得PM=BQ，可求得P点的纵坐标，利用抛物线解析式可求得P点坐标；(3)连接AC，设出P点坐标，则可表示出四边形PBAC的面积，再利用二次函数的性质可求得其最大值．

专题过关

1．如图，抛物线y=ax2+bx+c与坐标轴交点分别为A(﹣1，0)，B(3，0)，C(0，2)，作直线BC．

(1)求抛物线的解析式；

(2)点P为抛物线上第一象限内一动点，过点P作PD⊥x轴于点D，设点P的横坐标为t(0＜t＜3)，求△ABP的面积S与t的函数关系式．

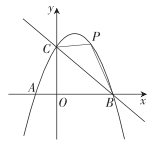
2.如图①，在平面直角坐标系中，已知抛物线y＝ax2＋bx－5与x轴交于A(－1，0)，B(5，0)两点，与y轴交于点C.

(1)求抛物线的函数解析式；

(2)若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标；

(3)如图②，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积．

3．如图，已知二次函数y=ax2+bx+3的图象交x轴于点A(1，0)，B(3，0)，交y轴于点C．

(1)求这个二次函数的解析式；

(2)点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；

(3)直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．

                      备用图

4.如图，在平面直角坐标系中，A，B为x轴上两点，C，D为y轴上的两点，经过点A，C，B的抛物线的一部分C1与经过点A，D，B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为(0，﹣3/2)，点M是抛物线C2：y=mx2﹣2mx﹣3m(m＜0)的顶点．

(1)求A,B两点的坐标；

(2)“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

(3)当△BDM为直角三角形时，求m的值．

5．已知直线y=1/2x+2分别交x轴、y轴于A，B两点，抛物线y=1/2x2+mx﹣2经过点A，和x轴的另一个交点为C．

(1)求抛物线的解析式；

(2)如图1，点D是抛物线上的动点，且在第三象限，求△ABD面积的最大值；

(3)如图2，经过点M(﹣4，1)的直线交抛物线于点P，Q，连接CP，CQ分别交y轴于点E，F，求OE•OF的值．

可打印word版(附答案)获取方式

长按关注，回复

5271

即可获取下载链接

▼

更多教研资源，长按下图关注后查看?

粉名校，您有眼光?