两个向量平行满足什么_数学的向量与物理的矢量

数学的向量与物理的矢量

一、概念

首先，从概念上看，矢量又称向量(Vector),最广义指线性空间中的元素.它的名称起源于物理学既有大小又有方向的物理量。

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量）。

数学的向量与物理的矢量的概念是一致的，运算法则也大多数适用于物理应用。

二、运算法则

下面我简单举例向量的加减法则，更多向量知识可以自己去看人教版的高中数必修四第二章。

向量的加减法则可以分为平行四边形法则与三角形法则，这个法则同样适用于物理应用中的矢量计算。

向量的平行四边形法则最早来源于物理中的力学。1586年，荷兰的斯蒂文在《静力学基础》一书中最早提出力的分解与合成原理。后来抽象到数学层面，就是向量的平行四边形法则。

如下图：

a,b两个向量相加，合就是a+b，假设a和b都是二维平面 的向量，其合就是上图中的平行四边形的对角线。（注意向量在印刷时，可以用加粗小写字母表示）

还有一个向量的三角形法则，如下图：

三、向量在物理中的应用

1.物理问题中的常见向量有力、速度、加速度、位移等，

2.动量mv涉及m与向量v的数乘运算

3.功是力F与其产生的位移S的数量积

4.但是注意区别物理中的向量与自由向量的区别。比如力向量不同于自由向量，它不仅包括大小方向，还有作用点。数学的大小相等方向相同的2个自由向量是相等的，因为自由向量可以平移。但是大小相等方向相同的2个力，如果作用点不同，那么它们不相等。

所以对于物理学应用题的力学的受力分析在向量的理解基础上，要重点分析不同作用点的影响。

5.物理学中的速度v，加速度a，位移s也是向量，例如数学常考的抛物线，在物理学上，就是因为重力加速度与初始速度方向不同导致的，那么为什么同样受到重力加速度影响，自由落体运动是直线，抛物线是曲线呢？这个区别在于自由落体运动的加速度和初始速度是同方向或方向相反的，抛物线的不同方向。

自由落体运动实验

基础例题：

综合例题：

四、用向量解决物理问题的步骤

1.抽象出物理问题中的向量，转化为数学问题

2.建立以向量为主体的数学模型

3.求出数学模型的解

4.回到物理问题，用求出的数值去解释相应的物理现象

五、常见物理矢量的解题思路

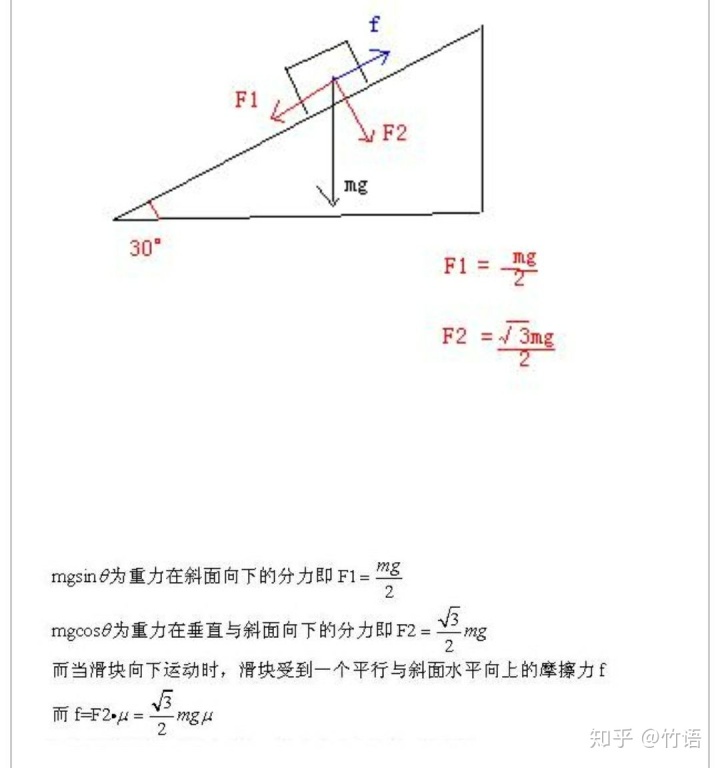
1.力向量：

（1）求作用于同一点的两个力的合力可以用平行四边形法则。

（2）对于同一个物体所受的力一般可以对力进行正交分解

（3）在同一平面，作用于同一点的几个力处于平衡状态，那么这几个力的向量和为零向量。

2.速度向量：

（1）可用求向量的加减运算法则，平行四边形法则求两个速度的合速度。

（2）初始速度与加速度不同方向时可以用平行四边形法则计算出运动曲线的每个点的瞬时速度，从而得到完整的运动曲线

（3）具体问题中需要对速度进行分解，可用平行四边形法则或正交分解法，具体由实际情况而定

3.力做功：

力做的功是力在物体前进方向上的分力与物体位移的乘积，即力和位移两向量的数量积，W=F.S，可以用投影法画图分析，计算数量积，｜F｜.｜s｜.cosa(a为力F与位移s的夹角。

作用点一致的，还可以建平面直角坐标系，转化成向量坐标计算

例如：

数学向量在物理中的应用

以上总结了向量在物理中的应用，原因在于我学生课间拿了高中物理题来问我，她对加速度，速度和位移的分析有些懵，我的物理从高考结束到现在有8年没碰过了，但是我用数学的向量逻辑给她演示一个分析方法，她就懂了。所以我才总结一下数学向量在物理中的应用。

这也是为什么提倡数学要重点训练学科思维逻辑分析能力的原因。知识的记忆也许会被时间淡化，但是思维逻辑分析能力会随着你而成长。