###
改进蚁群算法 MATLAB 实现代码
#### 自适应
蚁群算法简介
自适应
蚁群算法由 L. M. Gambardella 和 M. Dorigo 提出，旨在通过调整信息素挥发度提高基本
蚁群算法的性能[^1]。
#### 算法核心要素
该算法主要
改进在于动态调整信息素更新机制以及引入启发式因子 β 来平衡全局探索与局部开发之间的关系。当 β 较大时，算法更倾向于选择距离较短的路径；而当 β 设置为零时，则完全依赖于信息素浓度决定下一步方向[^4]。
####
MATLAB 代码示例
以下是基于上述原理编写的简化版本自适应
蚁群算法MATLAB实现：
```
matlab
function [bestPath, bestLength] = adaptiveACO(distMatrix, numAnts, alpha, betaStart, rhoMin, rhoMax, maxIter)
%
参数初始化
nCities = size(distMatrix, 1);
pheromones = ones(nCities); % 初始信息素分布均匀
% 记录最佳解及其长度
bestLength = inf;
for iter = 1:maxIter
% 动态调整β值 (这里简单线性变化作为示范)
beta = betaStart * (maxIter - iter) / maxIter;
paths = cell(numAnts, 1);
pathLengths = zeros(numAnts, 1);
% 构建每只蚂蚁的路径
for antIdx = 1:numAnts
currentCity = randi([1,nCities], 1); % 随机起点城市
visitedCities = currentCity;
while length(unique(visitedCities)) < nCities
nextCityProbabilities = calculateNextCityProbability(currentCity, ...
setdiff(1:nCities, visitedCities), distMatrix, pheromones, alpha, beta);
[~, nextCityIndex] = max(nextCityProbabilities);
nextCity = find(setdiff(1:nCities, visitedCities)==nextCityIndex)+min(setdiff(1:nCities, visitedCities))-1;
visitedCities(end+1) = nextCity;
currentCity = nextCity;
end
completeTourDistance = sumDistancesAlongPath(visitedCities, distMatrix);
paths{antIdx} = visitedCities;
pathLengths(antIdx) = completeTourDistance;
if completeTourDistance < bestLength
bestPath = visitedCities;
bestLength = completeTourDistance;
end
end
% 更新信息素水平
updatePheromoneLevels(paths, pathLengths, pheromones, rhoMin + (rhoMax-rhoMin)*rand(), distMatrix);
end
end
% 计算下一个城市的概率函数
function probabilities = calculateNextCityProbability(fromCity, toCities, distances, pheromones, alpha, beta)
attractiveness = arrayfun(@(city)(1/distances(fromCity, city)), toCities).^beta .* ...
pheromones(toCities).^(alpha);
totalAttractiveness = sum(attractiveness);
probabilities = attractiveness ./ totalAttractiveness;
end
% 求给定路径上的总距离
function distanceSum = sumDistancesAlongPath(path, distMatrix)
distanceSum = 0;
for i = 1:length(path)-1
fromCity = path(i);
toCity = path(mod(i,length(path))+1);
distanceSum = distanceSum + distMatrix(fromCity,toCity);
end
end
% 更新信息素矩阵
function updatePheromoneLevels(paths, lengths, pheromones, evaporationRate, distMatrix)
pheromones = (1-evaporationRate).*pheromones;
for k = 1:length(lengths)
thisPath = paths{k};
deltaTau = 1./lengths(k);
for j = 1:length(thisPath)-1
fromCity = thisPath(j);
toCity = thisPath(mod(j,length(thisPath))+1);
pheromones(fromCity, toCity) = pheromones(fromCity, toCity) + deltaTau;
pheromones(toCity, fromCity) = pheromones(toCity, fromCity) + deltaTau; %#ok<AGROW>
end
end
end
```
此段程序实现了自适应
蚁群算法的核心逻辑，并考虑到了不同阶段对于启发式因素的不同重视程度。具体来说，在迭代初期更多关注长远规划（较小的 β），随着搜索过程推进逐渐增加对当前最优方案的关注权重（增大的 β）。
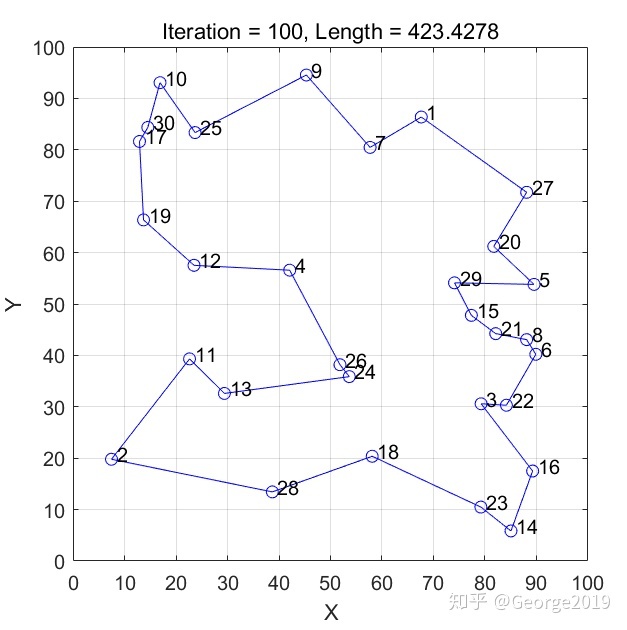
本文介绍了旅行商问题和蚁群算法的基本概念，并分享了一种改进的蚁群算法Matlab实现，强调了信息素更新规则的优化，引入了排名因子以提高算法效率。通过迭代收敛性测试，展示了算法在解决TSP问题上的性能。
最低0.47元/天 解锁文章
扫一扫
790
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
