em算法详细例子及推导_高斯混合模型(GMM)与EM算法的推导

欢迎访问本文英文版:

Gaussian Mixture Model and Expectation-Maximization Algorithm​wjchen.net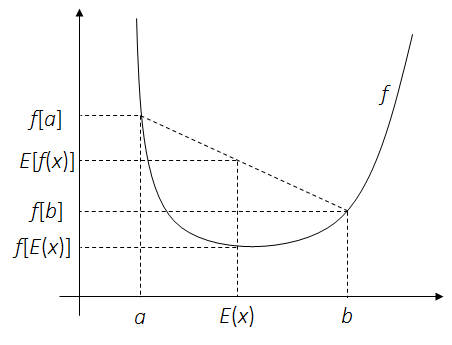

本文的Python代码实现放在在Github：

https://github.com/chenwj1989/MLSP/tree/master/gmm​github.com

1. 预备知识

1.1 高斯分布

高斯分布是拟合随机数据最常用的模型。单变量

的高斯分布概率密函数如下:

其中

• 分布的数学期望，
• 标准差，
• 是方差。

更一般的情况，如果数据集是d维的数据, 就可以用多变量高斯模型来拟合。概率密度是:

其中

• 是一个N×d的向量, 代表N组d维数据,
• 是一个1×d 的向量, 代表每维的数学期望,
• 是一个d×d的矩阵, 代表模型的协方差矩阵

1.2 Jensen不等式

这里给出随机分析里面Jensen's不等式的结论。在EM算法的求解过程中，Jensen不等式可以简化目标函数。

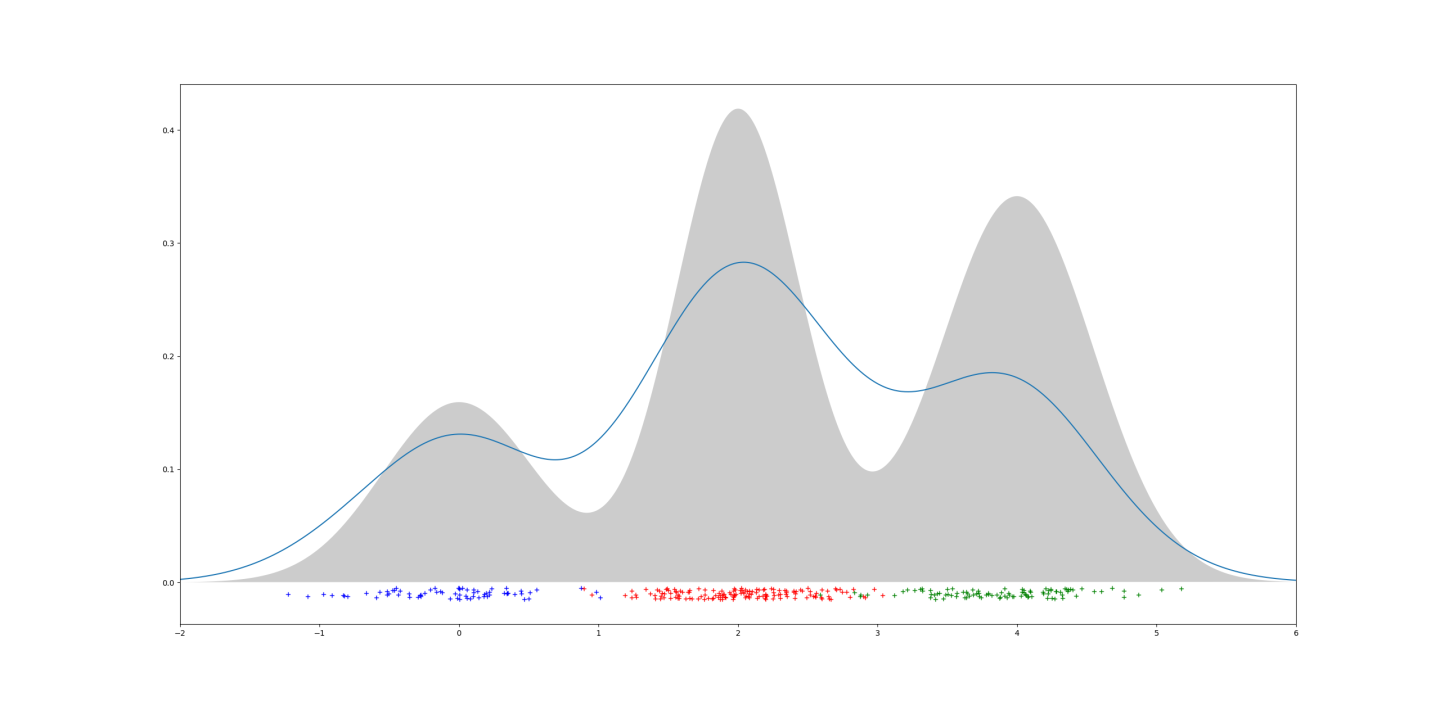
定理. 对一个凸函数

和随机变量

:

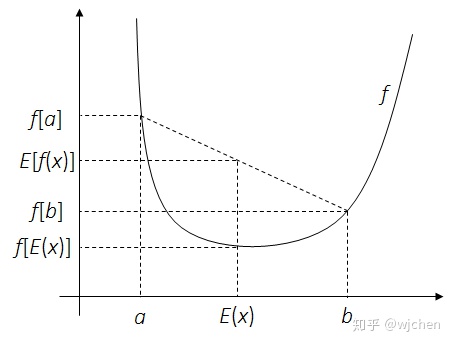
Fig.1 - 凸函数例子，设定

在a和b间均匀分布,

的期望总比

大。

定理. 对一个凹函数

和随机变量

:

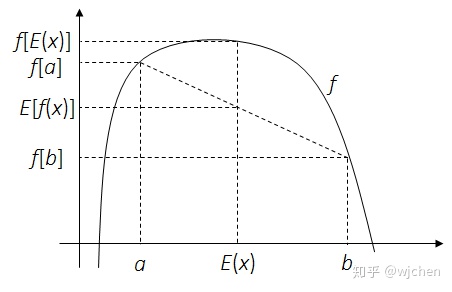
Fig.2 - 凹函数例子，设定

在a和b间均匀分布，

的期望总比

小。

1.3 矩阵求导

多维高斯混合模型的求解需要借助于矩阵和向量求导的公式。 下面是从 《The Matrix Cookbook》一书中摘录在推导过程中可能会用到的公式。

2.高斯混合模型和EM算法

2.1 高斯混合模型(GMM)

现实采集的数据是比较复杂的，通常无法只用一个高斯分布拟合，而是可以看作多个随机过程的混合。可定义高斯混合模型是

个高斯分布的组合，用以拟合复杂数据。

假设有一个数据集，包含了

个相互独立的数据：

, 这些数据看起来有

个峰，这样的数据集可用以下定义的高斯混合模型拟合：

Fig.3 - K=2的单变量GMM概率密度分布直方图

Fig.4 - K=2的双变量GMM例子

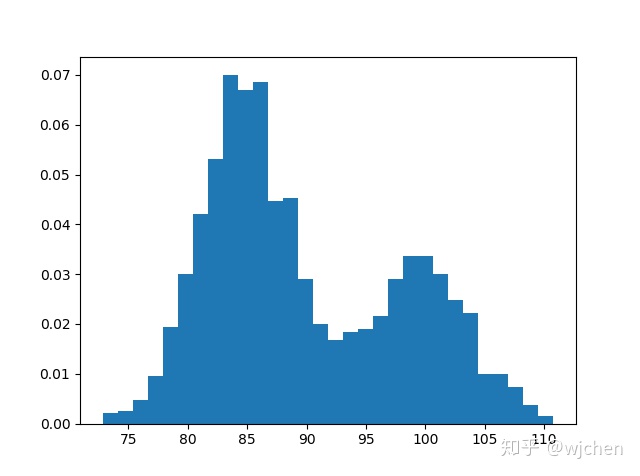
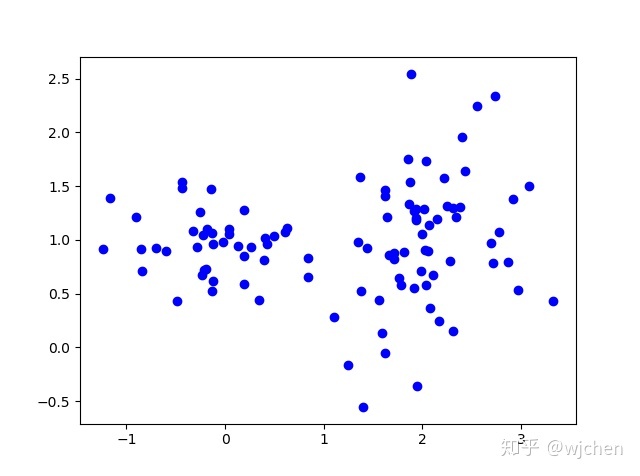
如果每一个数据点

都是d维的, 这些数据

如上图看起来分散在

个聚类，这种数据集可以用多变量高斯混合模型拟合。

其中

代表全体高斯模型参数,

是第

个高斯模型的先验概率, 各个高斯模型的先验概率加起来等于1。

2.2 EM算法

EM 算法是一种迭代的算法，算法解决的问题可如下表述：

• 采集到一组包含
  个独立数据的数据集
  。
• 预先知道、或者根据数据特点估计可以用
  个高斯分布混合进行数据拟合。
• 目标任务是估计出高斯混合模型的参数：
  组
  , or
  。

似然函数:

对于相互独立的一组数据, 最大似然估计(MLE)是最直接的估计方法。

个数据点的总概率可以表述成每个数据点的概率之乘积，这被称作似然函数

最大似然估计通过求似然函数的极大值，来估计参数

。

对高斯混合模型使用最大似然估计，求得的似然函数是比较的复杂的，单变量和多变量GMM似然函数结果如下，可以看到多变量GMM似然函数涉及多个矩阵的求逆和乘积等运算。所以要准确估计出

组高斯模型的参数，是很难的。

GMM 似然函数首先可以通过求对数进行简化，把乘积变成和。和的形式更方便求导和求极值。

隐参数:

是否对前面的对数似然函数进行求极大值，就可以求出目标的

组高斯模型参数了呢？我看到公式里面有两重求和，其中一重是在对数函数里面，直接求极值并不可行。

EM算法提出了用迭代逼近的方法，来对最优的高斯混合模型进行逼近。为了帮助迭代算法的过程，EM算法提出了隐参数

, 每次迭代，先使用上一次的参数计算隐参数

的分布，然后使用

更新似然函数，对目标参数进行估计。

在GMM估计问题中，EM算法所设定的隐参量

一般属于

。 用于描述

计算出GMM中

组高斯模型的参数后，某个数据点

属于第

个高斯模型的概率:

把隐参量

引入到第

个数据的概率估计中：

跟高斯混合分布

作对比, 发现

就是

的先验分布

。

而在

条件下的

的条件概率就是第

个高斯模型。

现在可以把隐参量代入到对数似然函数中。可以加入冗余项：隐参数在数据

和高斯参数下的后验概率，从而引入Jensen不等式来简化似然函数。

似然函数简化:

下面通过Jensen不等式简化对数似然函数。

对照Jensen不等式，让

。

得到

于是似然函数简化成对数函数的两重求和。等式右侧给似然函数提供了一个下界。

我们可以根据贝叶斯准则进行推导其中的后验概率

定义

那么

不等式的右侧给似然函数提供了一个下界。EM算法提出迭代逼近的方法，不断提高下界，从而逼近似然函数。每次迭代都以下面这个目标函数作为优化目标：

这个式子表示，在第

次迭代后，获得参数

，然后就可以计算隐参数概率

。 将隐参数代回

, 进行最大似然优化，即可求出更优的参数

。

迭代求解:

迭代开始时，算法先初始化一组参数值

, 然后间隔地更新

和

。

• 经过
  轮迭代,已获得一组目标参数
  临时的值。
• 基于当前的参数
  ，用高斯混合模型计算隐参数概率
  。然后将隐参数概率代入对数似然函数，得到似然函数数学期望表达式。这一步叫
  expectation step。
• 如前文使用Jensen推导得出，得到每次更新了隐参数
  后的目标函数是：
• 利用
  当前值, 最大化目标函数，从而得出新一组GMM参数
  。 这一步叫作
  maximization step。

3.EM算法解单变量GMM

单变量 GMM使用EM算法时，完整的目标函数为

3.1 E-Step:

E-step目标就是计算隐参数的值， 也就是对每一个数据点，分别计算其属于每一种高斯模型的概率。 所以隐参量

是一个N×K矩阵。

每一次迭代后

都可以用最新的高斯参数

进行更新。

E-step 就可以把更新的

代入似然函数，得到目标函数的最新表达。该目标函数展开如下：

3.2 M-Step:

M-step的任务就是最大化目标函数，从而求出高斯参数的估计。

更新

:

在高斯混合模型定义中，

受限于

。所以

的估计是一个受限优化问题。

这种问题通常用拉格朗日乘子法计算。下面构造拉格朗日乘子：

对拉格朗日方程求极值，也就是对

求导数为0处，该点就是我们要更新的

值。

将所有

项累加, 就可以求得

。

于是利用地

次迭代的隐参量，我们就得到了

在

次迭代的更新方程：

更新

:

并没有类似

的限制条件，可以直接把目标函数对

求导数：

让

, 得到

所以在

次迭代，

就用全部

的加权平均来求得，权值正是

属于第

个模型产生的概率

。

更新

:

类似地, 将目标函数对

求极大值：

让导数为0：

得到

高斯模型里面使用的都是

，所以就不需要求平方根了。

的更新方程如下，依赖于更新的

。 所以一般都是先把

算出来，然后再更新

。

4.EM算法解多变量GMM

同样的，我们可以得到每次迭代的目标函数如下：

其中

• 是1×d的向量,
• 是一个0和1间的值,
• 是1×d的向量,
• 是d×d的矩阵,
• 是N×K的矩阵。

4.1 E-Step:

跟单变量GMM一样，E-step计算隐参数，但是需要用多维高斯分布，利用了多维矩阵乘法和矩阵求逆，计算复杂度要大很多。

目标函数更新如下：

4.2 M-Step:

更新

:

多变量GMM下，

的更新跟单变量 GMM一样。

得到完全一样的更新方程：

更新

对

求导，得到

实数协方差矩阵

对称的, 其逆矩阵也是对称的。 于是我们可以利用第一部分列出的公式

求偏导数。

所以

的更新方程同样是

的加权平均，只是这时候

is a 1×d 向量。

更新

:

让导数

, 得到

协方差矩阵

是对称的,可以利用第一部分的矩阵求导公式

和

，求得极大值

。

类似地, 我们可以得到

在第

次迭代的更新方程, 它依赖于

。所以我们需要先计算

，然后更新

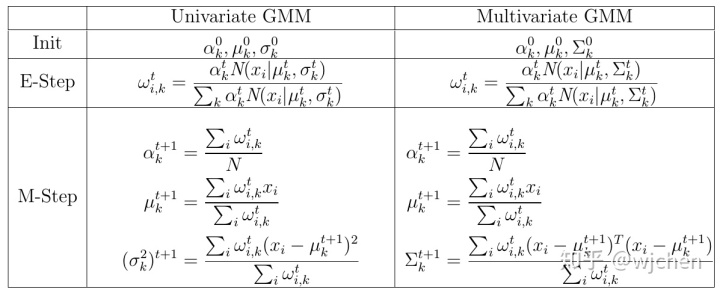
5.总结

6.代码实现

GMM-EM算法的实现和测试代码上传到GitHub仓库，下面是算法主函数的代码

def