正则 不等于_物理的世界——正则角动量守恒

一、引言

笔者对处于匀强磁场中，只受到洛伦兹力的带电粒子“正则角动量守恒”这一问题的思考最初来源于第三十五届全国中学生物理竞赛复赛第五题(图1)的题目设置中。题目中“为了方便起见，将B的参数化为

”这一前提条件在题目中起到点睛之笔的作用。而笔者在物理竞赛培训过程中，也曾接触过利用“正则动量守恒”巧解题目的处理办法，因此笔者试图利用类比的思想得到“正则角动量守恒”的处理办法。在2019年4月16日，笔者成功求得了这一方程。但笔者在大学生涯中接触到了分析力学和电动力学部分内容，并遗憾地得知这一方程仅是在特殊情况下的磁场中带电粒子的广义动量守恒的简单形式，并非笔者原创。在此将电动力学形式的推导过程一并给出，算为这一问题的思考暂时画上句号。

二、正则动量守恒

 在叙述“正则角动量守恒”的推导思路前，有必要先对正则动量守恒的推导进行简单的介绍。处于匀强磁场中，只受到洛伦兹力的带电粒子的动力学方程有，显然这一动力学方程是牛顿第二定律的微分形式，而我们在解题过程中利用积分形式的动力学方程则更为方便，同时我们更希望这一方程还是具有守恒意义的，以体现物理解题的美感，因此我们便引入“正则动量守恒”这一辅助解题的工具。

  我们尝试将带电粒子的动力学方程分解为相互垂直的两个方向的方程：

对方程左右两边同时对时间求不定积分得到：

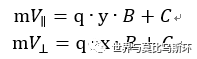
移项可得：

注意到这一项

结果等于常数，因此我们找到了处于匀强磁场中，只受到洛伦兹力的带电粒子的一个物理学守恒量，我们姑且将其称为“正则动量”。

我们可以利用这个方程巧解2015年天津高考理科综合物理部分第14题。这里用第(3)小问的求解过程作为正则动量方程应用的例子。

对竖直方向列“正则动量守恒方程”有：

对带电粒子列动能定理有：

由于粒子恰好不能从右侧边界穿出，所以有运动学补充方程：

V=V垂直

解得：

所以比荷较大的粒子不能穿出右边界。

  与原答案相比较，正则动量这一处理方法较好地利用了题目所给出的边界条件，守恒式的简洁性也给解题带来了方便。而且我们也不难发现，正则动量守恒有两个方向相互垂直的的方程，这里我们却只选择了其中一个方程使用，原因在于对于题目所给物理情景而言，多层紧密相邻的电场和磁场具有上下平移的不变性。诺特定理指出，连续对称性和守恒定律一一对应，我们在发现对称性并利用该对称性解题，无疑是最灵活地运用题目所给条件的做法。因此正则动量在具有向一个平移的对称性的题目中，往往是最简便的方式。

-----------------------------------------------------------

关于正则角动量守恒我们仍有很多方面可以深入探讨，但笔者精力和能力有限，超越普通物理层次的部分仍未完笔，本文为笔者高中阶段研究所得，所用知识也不超出高中生的理解范围，若有不当之处烦请批评指正。

原预定公众号的更新的文章实为《物理的世界——量纲分析》，为笔者读赵凯华老师《定性半定量物理学》心得体会，但由于公众号编辑公式实在不便(需要编辑后截图上传)，写作计划也多次搁浅，可能将以其他形式呈现给大家。

在寒假期间笔者曾多次参加《大学物理》习题课的讲解，其课程内容设计也多有用心之处，其文稿或能整理并发布。另外笔者读费恩曼传也多有所得，也需整理一段时间才能与各位见面。

关于每日一题系列，合集也在整理当中，会逐渐从微信朋友圈移至公众号更新。笔者的更新计划大致如上。