已知圆上任意两点求圆心和半径_寻动点轨迹，求几何最值难题

近些年的中考中，经常出现动点的运动轨迹类问题，通常出题以求出轨迹的长度或最值最为常见。很多考生碰到此类试题常常无所适从，不知该从何下手。

其实初中阶段如遇求轨迹长度仅有2种类型："直线型"和"圆弧型"(两种类型中还会涉及点往返探究"往返型")，对于两大类型该如何断定，通常老师会让学生画图寻找3处以上的点来确定轨迹类型进而求出答案，对于填空选择题而言不外乎是个好方法，但如果要进行说理很多考生难以解释清楚。

典型考题

类型1 轨迹为直线型最值问题

1．(2019春•姑苏区期末)如图，正方形纸片ABCD的边长为4cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的最大值是(　　)

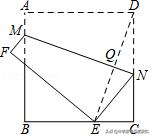
A．2 cm B．4 cm C．√2 cm D．1 cm

【解析】如图，取AB、CD中点K、G，连接KG、BD交于点O．

由题意可知点Q运动的路线就是线段OG，

∵DO＝OB，DG＝GC，∴OG＝1/2BC＝1/2×4＝2．

∴点Q移动路线长度的最大值是2．故选：A．

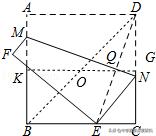
2．(2018秋•西安期末)如图，在平面直角坐标系中，x轴上有一点B(10，0)，点M由点B出发沿x轴向左移动，以BM为斜边在x轴上方作等腰直角三角形AMB，则点M在运动过程中，OA的最小值为_________．

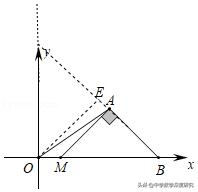
【解析】：如图，过点O作OE⊥AB于点E，

∵△AMB是等腰直角三角形，∴∠ABM＝45°，

∴点A在与OB成45°角的直线BE上移动，

∴当点A与点E重合时，OA的值最小，

∵OE⊥AB，∠ABO＝45°，

∴∠EOB＝45°＝∠EBO，∴OE＝BE，

∴OB＝√2OE＝10，∴OE＝5√2，∴OA的最小值为5√2．

3．(2019•常熟市二模)已知x轴上一点A(1，0)，B为y轴上的一动点，连接AB，以AB为边作等边△ABC如图所示，已知点C随着点B的运动形成的图形是一条直线，连接OC，则AC+OC的最小值是_______．

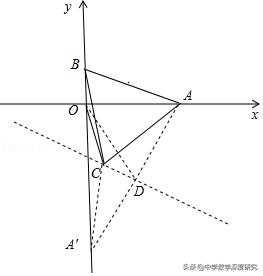
【解析】如图所示，在第四象限以OA为边长作等边△AOD，

连接OD，并作直线CD，延长AD交y轴于点A'．

∵等边△ABC、等边△AOD，

∴AB＝AC，AO＝AD，∠BAC＝∠OAD＝60°。

∴∠BAC﹣∠OAC＝∠OAD﹣∠OAC，∴∠BAO＝∠CAD.

在△BAO和△CAD中，AB=AC, ∠BAO＝∠CAD,AO=AD，

∴△BAO≌△CAD(SAS),∴∠AOB＝∠ADC.

∵∠AOB＝90°,∴∠ADC＝90°,∴CD⊥AD.

∴点C随着点B的运动形成的图形是直线CD.

∵∠AOA'＝90°，∠OAD＝60°,

∴∠AA'O＝30°. ∴OA＝1/2AA',∴AD＝OA＝1/2AA',

∴点D是AA'的中点.

∵CD⊥AD,∴CD是AA'的中垂线.∴AC＝A'C,∴AC+OC＝A'C+OC.

又∵点C在直线CD上运动，所以点O、C、A'三点共线时，A'C+OC的值最小，最小值为OA'的长．

在R△AOA'中，∠AOA'＝90°，∠OAD＝60°，OA＝1，OA'＝√3OA＝√3，

∴AC+OC的最小值为√3．

故答案为√3．

类型2 轨迹为圆弧型最值问题

4．(2018秋•德清县期末)如图，以G(0，2)为圆心，半径为4的圆与x轴交于A，B两点，与y轴交于C，D两点，点E为⊙G上一动点，且点E在第一象限，CF⊥AE于点F，当点E在⊙G的圆周上运动的过程中，线段BF的长度的最小值为(　　)

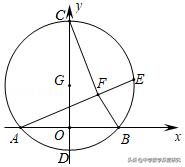
A．3 B．2√3﹣2 C．6﹣2√3 D．4﹣√3

【解析】：连接AC、BC，如图所示：

∵以G(0，2)为圆心，半径为4的圆与x轴交于A，B两点，与y轴交于C，D两点，

∴OC＝6，OG＝2，AG＝4，OA＝OB，AC＝BC，

5．(2019•南充中考题)如图，矩形硬纸片ABCD的顶点A在y轴的正半轴及原点上滑动，顶点B在x轴的正半轴及原点上滑动，点E为AB的中点，AB＝24，BC＝5．给出下列结论：①点A从点O出发，到点B运动至点O为止，点E经过的路径长为12π；②△OAB的面积最大值为144；③当OD最大时，点D的坐标为(25√26/26，125√26/26)．其中正确的结论是______．(填写序号)

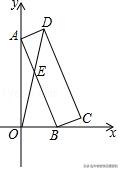
【解析】①由条件可知AB＝24，则AB的中点E的运动轨迹是圆弧，最后根据弧长公式即可计算出点E所经过的路径长；②当△OAB的面积最大时，因为AB＝24，所以△OAB为等腰直角三角形，即OA＝OB，可求出最大面积为144；③当O、E、D三点共线时，OD最大，过点D作DF⊥y轴于点F，可求出OD＝25，证明△DFA∽△AOB和△DFO∽△BOA，可求出DF长，则D点坐标可求出．故答案为：②③．

6.(2019秋•河西区期末)如图，在边长为1的正方形ABCD中，将射线AC绕点A按顺时针方向旋转α度(0＜α≤360°)，得到射线AE，点M是点D关于射线AE的对称点，则线段CM长度的最小值为______．

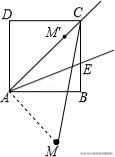
【解析】：如图所示：连接AM．∵四边形ABCD为正方形，∴由勾股定理可求得AC＝√2．∵点D与点M关于AE对称，∴AM＝AD＝1．

∴点M运动的轨迹是在以A为圆心，以AD长为半径的圆上．

如图所示，当点A、M、C在一条直线上时，CM有最小值．∴CM的最小值＝AC﹣AM′＝√2﹣1，故答案为：√2﹣1．

7．(2019秋•南通期中)如图，AB为半圆O的直径，点C在半圆O上，AB＝8，∠CAB＝60°，P是弧BC上的一个点，连接AP，过点C作CD⊥AP于点D，连接BD，在点P移动过程中，BD长的最小值为______．

方法归纳

直线型轨迹如何寻，任画三点定轨迹，此法适用选填题，要知它法往下寻。

如遇定点和定角，夹角定位来搞定，如遇定线和定距，平行定距把它解。

圆弧型轨迹如何寻，通过定点+定长⇒圆, 定线+定角⇒圆两个模型确定。

动点路径问题中，核心方法是寻找定点、定线、定长、定角等，再根据线与圆的基本概念及基本性质确定运动轨迹所形成的图形.