c++求区间第k大数_时间序列分析第13讲（递推预测例子，参数估计三种方法，AR定阶初步）...

ARMA 序列递推预报例子

考虑下面的 ARMA(4,2) 模型

利用 wold 系数以及自协方差函数的公式

编程计算出前 21 个自协方差

加到无穷大可以用加到 50 来近似

计算自协方差的结果为

利用上一讲得到的公式计算 Yt 的自协方差函数：

利用递推预报公式对 Y 进行预报，结果如下图

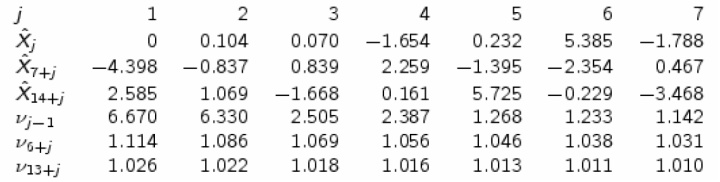
注意：预测误差趋于 1 （实际上是白噪声方差）的速度还是很理想的

以下为递推预报前20（红）与真实结果（蓝）

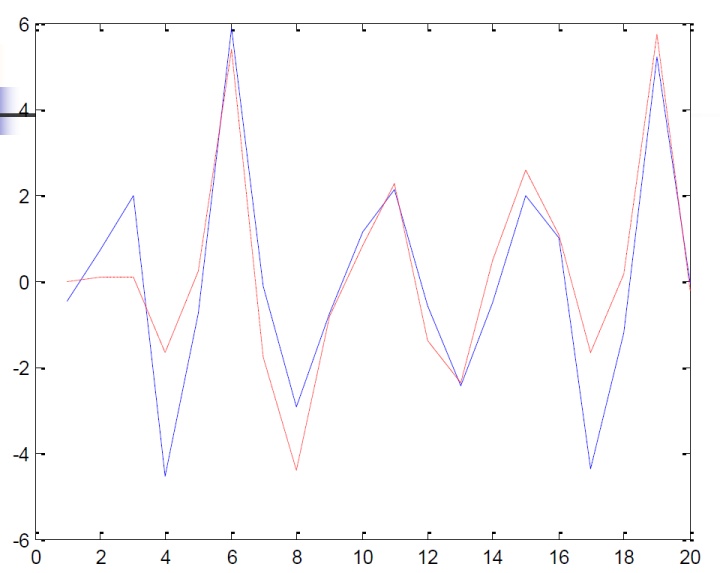
ARMA(2,1)例子 （考试形式）

考察如下模型

计算 wold 系数得到

两边同乘 Xt-k 然后取数学期望

类似第 05 讲的方法，可以得到自协方差函数为

解出 C1 和 C2 即可

作 Ansley 变换

计算 Y 的自协方差函数如下

• 当 s 和 t 都不超过 2，那么自协方差函数与 X 的一样
• 当一个超过 2 一个不超过，根据 Ansley 变换下 Y 的定义计算（基本上就是 Y-W 方程的结果）
• 两个都超过 2，为 MA 序列。相差超过 1 为 0，不超过 1 则根据 b0 和 b1 计算即可

接下来手算

即均方误差,其中

由于白噪声方差为 1，所以对 X 的预测误差等于对 Y 的预测误差

第一个预测误差即

，然后两边同乘取期望来求系数

再递推第二步

注意：EY3Y1 = 0 是凑巧！对于其他 ARMA 模型还是要将 Y2 尖用之前的递推结果替换.

最后一个：用预测误差来表示

的自协方差矩阵的行列式。

这个留到第六章讲完之后再做

第六章 ARMA 模型参数估计

用各类统计软件都能很方便的实现参数估计，所以我们注重理论的推导。

6.1 AR 模型的参数估计

需要估计的参数有 a1 到 ap 以及白噪声方差。

（一）Y-W 估计

得到数据后，首先进行中心化。先假定服从 AR(p) 模型，p 已知。

然后计算样本协方差函数 0 到 p。

解 Y-W 方程可以得到系数和白噪声方差的估计

为了避免计算这个矩阵的逆，之前也介绍过 Levinson 递推法

优点：计算简单，保证最小相位性

Y-W估计的相合性

由于 AR(p) 总体自协方差函数正定，所以系数和白噪声方差是总体自协方差的连续函数。而当白噪声独立同分布时，样本自协方差是总体自协方差的强相合估计，所以 Y-W 估计的系数和白噪声方差也具有强相合性。

以下给出关于 Y-W 估计性质的定理（了解就可）

定理的 2 和 3 分别给出了渐近正态性以及重对数阶的收敛速度。

有渐近正态性就可以计算置信区间了。

（二）最小二乘估计

基本思想是使得残差平方和达到最小

记

根据回归理论，最小二乘解为

，解唯一的条件为

正定

最小二乘估计的计算更简单，甚至不用计算自协方差。

（三）依概率有界

实际模拟出来，Y-W 估计和最小二乘估计的结果差不多，下面理论说明这一点。

定义 ξ 为时间序列，如果存在正数 M ，对任意正数 ε 有

称时间序列 ξ 是依概率有界的，记作

，如果

，就称

，其中 cn 为非零常数

注意这里是大 O，如果依概率收敛于 0 则记作小 o。

引理 依概率收敛包含在依概率有界中。

证明思想 N 很大时有界，而前面有限项总存在最大值，所以整体有界。

引理 如果时间序列依概率有界，常数列 cn 趋于无穷，那么

证明思想 有界的除以趋于无穷大的，极限显然为 0
对于一个确定的随机变量（不是广义的），只要期望有界，它就是依概率有界的。

引理 时间序列同分布，一阶矩存在，那么依概率有界。

证明 既然同分布，就可以当做一个确定的随机变量

（四）Y-W 估计与最小二乘估计的比较

回顾一下 Y-W 估计与最小二乘估计的形式

考察矩阵

的第 j 行第 k 列元素

其中矩阵乘法的形式如下，由于两个矩阵是转置关系，所以等价第 j 行乘第 k 行

得到的

为样本协方差，所以 Y-W 估计的系数矩阵与最小二乘估计的系数矩阵之间的差异为

求和都只有有限个，所以都会趋于 0，但第二项会啰嗦一些，因为求和指标也在变化。

说明：第一项中

是固定的随机变量，依概率有界。除以 N 后与 1/N 同阶。

第二项用 AR 序列的严平稳遍历性，得到

也是严平稳遍历的。

第一个等号相当于将 a 到 b 分为 1 到 b 减去 1 到 a； 其中最后一行用到严平稳遍历性。

下面考察两种估计方程的右端项差异，计算下面矩阵的第 j 个元素

同样可以得到

类似地，右端项的差异也是与 1/N 同阶的。

因此，由 Y-W 的强相合性可得最小二乘估计的强相合性。

下面比较两种估计得到的系数之间的差异，以及收敛速度差异。

作出两者的差并计算得到

第二个等式为添一减一，其中第一项有一个依概率有界的因子，第二项配凑依概率有界因子得到第三个等式。

由于 1/N 收敛到 0 的速度很快，所以对较大的 N，两种估计方法没有很大差异。

实际模拟中，样本较小时，系数估计是 Y-W 比较好，预测方差估计是最小二乘法比较好；样本较大时没有明显差异

（五）最小二乘估计的极限分布

最小二乘估计与 Y-W 估计有相同的渐近分布：

（六）极大似然估计

假定白噪声服从正态分布，那么

的联合密度为

注意白噪声下标不是从 1 开始的

将白噪声用原序列 X 替换得到 X 的似然函数

下面先对数据进行中心化，然后求对数似然的极值点。

可以发现，

为最小二乘估计的极小化目标，所以最大似然估计与最小二乘估计得到的系数是一样的。而白噪声方差可以通过求偏导，并令为 0 得到

三种估计方法考试以叙述题的形式出现。

（七）AR 模型的定阶问题

思想：计算偏相关系数，观察是否有截尾性

此外，用的很多的还有 AIC 和 BIC 准则，即定义某个与模型拟合优度和简单程度有关的信息量，阶数 p 使得模型拟合程度最好。

通过样本，利用 Levinson 递推来计算偏相关系数，可以得到偏相关系数的强相合估计（在白噪声独立同分布假定下）。（利用样本自协方差函数的强相合性）

（1）偏相关系数检验

通过递推计算的（也可以解 Y-W 方程）偏相关系数有渐近正态性

当 k > p 时，

渐近服从标准正态，所以只要对某个 p 的偏相关系数没有落在标准正态置信区间中，而 p+1 的偏相关系数落在标准正态置信区间中，就可以将阶数定为 p.

证明标准正态：只要说明

第 k 行第 k 列元素为 1 即可。

这里只考察第 1 行第 1 列元素与第 k 行第 k 列元素的伴随矩阵，这两个元素的伴随矩阵是一样的。

于是

的左上角元素与右下角元素一样

回顾 AR 序列的 YW 方程

从而

注意比较等式两端的最上方，于是

（2）用样本偏相关系数定阶

取 p 为最大位于置信区间外的数

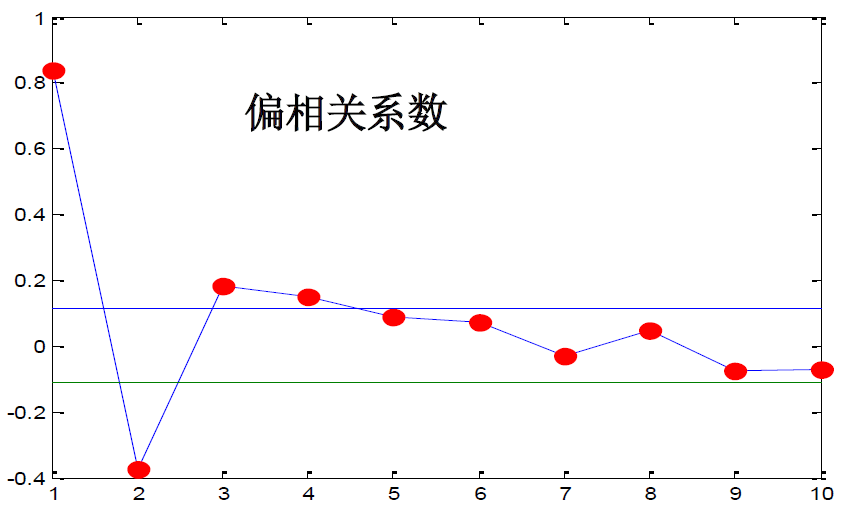
对于上图，定阶为 4

（3）AIC 和 BIC 定阶

两个信息量都考察了拟合优度与模型简单程度

其中 p0 为阶数的上界，k 是阶数（阶数越高则模型越复杂）。

自然希望 AIC 和 BIC 越小越好，取极小值对应的 k 作为阶数。

两者差异体现在对参数个数的惩罚上，统计中这样的惩罚项都是先随意取，发现实际效果好再来解释。