(作者:陈玓玏)
1. 损失函数
假设我们使用0-1损失函数,函数表达式如下:

Y
Y
Y为真实值,有
c
1
,
c
2
,
.
.
.
,
c
K
{c_1,c_2,...,c_K}
c1,c2,...,cK这
K
K
K个类标记,
f
(
X
)
f(X)
f(X)是决策函数,其输出值就是类标记的预测值,那么对应的代价函数,也就是期望损失函数为:
R
e
x
p
(
X
)
=
E
(
L
(
Y
,
f
(
X
)
)
)
R_exp(X) = E(L(Y,f(X)))
Rexp(X)=E(L(Y,f(X)))
因为这里的期望是对联合概率取的,所以有如下关系:
R
e
x
p
(
X
)
=
∑
k
=
1
K
L
(
c
k
,
f
(
X
)
)
P
(
c
k
,
X
)
=
E
x
∑
k
=
1
K
L
(
c
k
,
f
(
X
)
)
P
(
c
k
∣
X
)
R_exp(X) = \sum_{k=1}^{K}L(c_k,f(X))P(c_k,X) = E_x\sum_{k=1}^{K}L(c_k,f(X))P(c_k|X)
Rexp(X)=k=1∑KL(ck,f(X))P(ck,X)=Exk=1∑KL(ck,f(X))P(ck∣X)
将
L
(
Y
,
f
(
X
)
)
L(Y,f(X))
L(Y,f(X))代入,得到:
R
e
x
p
(
X
)
=
∑
k
=
1
K
P
(
Y
≠
c
k
∣
X
)
=
∑
k
=
1
K
(
1
−
P
(
Y
=
c
k
∣
X
)
)
R_exp(X) = \sum_{k=1}^{K}P(Y \neq c_k|X) = \sum_{k=1}^{K}(1-P(Y=c_k|X))
Rexp(X)=k=1∑KP(Y̸=ck∣X)=k=1∑K(1−P(Y=ck∣X))
要让损失函数最小化,只需要和项中的每一项都是最小即可:
m
i
n
∑
k
=
1
K
(
1
−
P
(
Y
=
c
k
∣
X
)
)
=
m
a
x
∑
k
=
1
K
P
(
Y
=
c
k
∣
X
)
=
m
a
x
P
(
Y
=
c
k
∣
X
)
min\sum_{k=1}^{K}(1-P(Y=c_k|X)) = max\sum_{k=1}^{K}P(Y=c_k|X) = maxP(Y=c_k|X)
mink=1∑K(1−P(Y=ck∣X))=maxk=1∑KP(Y=ck∣X)=maxP(Y=ck∣X)
这也就是我们之后朴素贝叶斯算法的依据:求得最大后验概率即能最小化代价函数!
2. 求最大化后验概率
基于上面的分析我们知道,对于数据集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) D = {(x_1,y_1),(x_2,y_2),...,(x_N,y_N)} D=(x1,y1),(x2,y2),...,(xN,yN),当 y i y_i yi的可取值为 c 1 , c 2 , . . . , c K {c_1,c_2,...,c_K} c1,c2,...,cK时,我们对每个样本 x i x_i xi求其对应不同类标记 c k c_k ck的后验概率值,并选择最后的后验概率值对应的类标号 c k c_k ck作为样本的分类结果,我们就能以最小的代价函数获得最优的分类。
那么,我们可以根据贝叶斯公式来求后验概率:
P
(
Y
=
c
k
∣
X
=
x
i
)
=
P
(
X
=
x
i
∣
Y
=
c
k
)
P
(
Y
=
c
k
)
∑
k
=
1
K
P
(
X
=
x
i
∣
Y
=
c
k
)
P
(
Y
=
c
k
)
P(Y=c_k|X=x_i) = \frac{P(X=x_i|Y=c_k)P(Y=c_k)}{\sum_{k=1}^{K}P(X=x_i|Y=c_k)P(Y=c_k)}
P(Y=ck∣X=xi)=∑k=1KP(X=xi∣Y=ck)P(Y=ck)P(X=xi∣Y=ck)P(Y=ck)
这里有些犯难了,样本
x
i
x_i
xi有
J
J
J个属性,怎么求得先验概率呢?这时候朴素贝叶斯的优势就体现出来了,朴素贝叶斯和贝叶斯最重要的区别就在于,朴素贝叶斯假设在类确定的条件下,样本的特征之间是相互独立的!因此,上面的公式就可以拆分成以下形式:
P
(
Y
=
c
k
∣
X
=
x
i
)
=
P
(
Y
=
c
k
)
∏
j
=
1
J
P
(
X
j
=
x
i
j
∣
Y
=
c
k
)
∑
k
=
1
K
P
(
Y
=
c
k
)
∏
j
=
1
J
P
(
X
j
=
x
i
j
∣
Y
=
c
k
)
P(Y=c_k|X=x_i) = \frac{P(Y=c_k)\prod_{j=1}^{J} P(X^j=x_i^j|Y=c_k)}{\sum_{k=1}^{K}P(Y=c_k)\prod_{j=1}^{J} P(X^j=x_i^j|Y=c_k)}
P(Y=ck∣X=xi)=∑k=1KP(Y=ck)∏j=1JP(Xj=xij∣Y=ck)P(Y=ck)∏j=1JP(Xj=xij∣Y=ck)
因为分母对于同一个样本来说都是一样的,因此我们在具体算法流程中是可以不考虑分母的大小的。
3. 极大似然完成参数估计
在上一小节,我们已经计算好了最大后验概率的公式,但是公式中还有两个重要的部分没有得到解答,一个是类别概率,一个是先验概率,我们通过极大似然估计来完成这两个参数的估计:

完成先验概率及条件概率的估算后,我们就可以完成后验概率(不需要计算分母)的计算了。针对不同的类标号计算后验概率,计算结果最大的后验概率对应的类标号即为样本对应的类标号。
4. 贝叶斯估计
用极大似然估计的先验概率及条件概率可能出现概率值为0的情况,比如计算先验概率时,发现没有
c
k
c_k
ck类型的样本,那么先验概率
P
(
Y
=
c
k
)
P(Y=c_k)
P(Y=ck)的估计结果将会为0,那么条件概率
P
(
X
j
=
a
j
l
∣
Y
=
c
k
)
P(X^j=a_{jl}|Y=c_k)
P(Xj=ajl∣Y=ck)的分母将会为0,计算不出结果,后验概率自然也就无法计算了。这种情况下,可以在条件概率中加入一个参数来做平滑,公式如下:
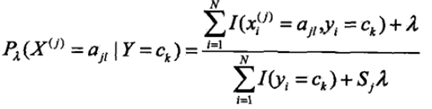
式中
s
j
s_j
sj为样本的第
j
j
j个特征的可取值个数,也就是可取值
a
j
1
,
a
j
2
,
…
,
a
j
S
j
a_{j1}, a_{j2},…, a_{jS_j}
aj1,aj2,…,ajSj的个数,
λ
=
0
\lambda=0
λ=0时,公式就是条件概率的极大似然估计,
λ
=
1
\lambda=1
λ=1时,称为拉普拉斯平滑。对先验概率也要做平滑:
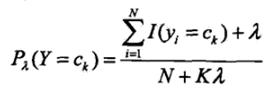
式中
N
N
N为样本个数,
K
K
K为类标号个数。
5. 朴素贝叶斯使用场景
(个人理解,有不对请提出来讨论,谢谢)朴素贝叶斯适用于给文章加标签这样的场景,假设有十万篇文章需要加标签,我们可以先对每篇文章进行分词,提取重复度高的关键词,然后生成关键词向量,如下表所示:

下表提取了文章中出现频率最高的关键词,并根据事先定义好的关键词向量,如果这个关键词在文中出现频率高,则标记为1,频率不高,则标记为0,然后就可以通过朴素贝叶斯算法进行分类了。比如新来一篇文章6,其出现频率最高的关键词是“吃饭”,我们需要分别计算
P
(
“
经
济
”
∣
文
章
6
)
P(“经济”|文章6)
P(“经济”∣文章6),
P
(
“
美
食
”
∣
文
章
6
)
P(“美食”|文章6)
P(“美食”∣文章6),…,
P
(
“
数
据
分
析
”
∣
文
章
6
)
P(“数据分析”|文章6)
P(“数据分析”∣文章6),根据公式计算就好。
我也想过是不是不用是否出现作为特征的值,而是用出现的频率作为特征的值,但是这样的话每个特征可取的值就非常多,计算条件概率时会很复杂,所以还是采用了这种造变量的方法。
6. 朴素贝叶斯优缺点
优点:计算简单,高效;
缺点:分类性能不一定高,要求特征相互独立的条件太强。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








