相信大家对三角形的面积,平行四边形以及矩阵的面积求法都不陌生。而对于一般的四边形面积该如何求得呢?古印度数学家婆罗摩笈多曾给出四边形的面积公式为 从形式上看和三角形的面积公式——海伦公式很像,只是婆罗摩笈多,并没有意识到他给出的这个四边形面积公式是内接四边形的面积公式。那么一般的四边形面积公式是什么样的呢?再从一般到特殊,导出平行四边形和矩形的面积。
从形式上看和三角形的面积公式——海伦公式很像,只是婆罗摩笈多,并没有意识到他给出的这个四边形面积公式是内接四边形的面积公式。那么一般的四边形面积公式是什么样的呢?再从一般到特殊,导出平行四边形和矩形的面积。
四边形的面积
已知四边形ABCD中 ,面积为S,半周长为p,求证:
,面积为S,半周长为p,求证:

证明: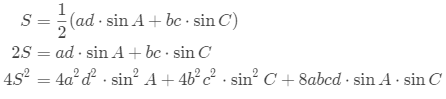 由余弦定理可得
由余弦定理可得 第一个式子两边乘以4后与第二个式子相加,可得
第一个式子两边乘以4后与第二个式子相加,可得
由第一个式子可得: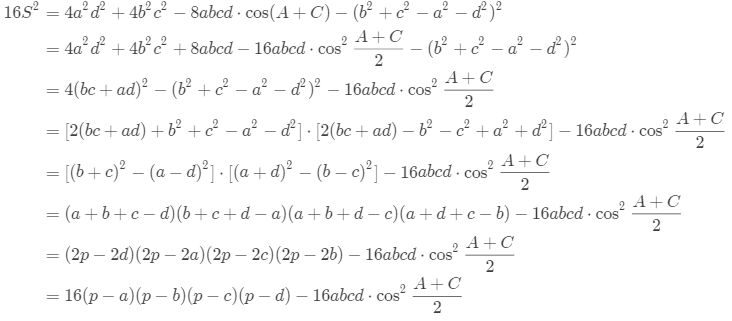 所以
所以
平行四边形与矩形面积
若四边形为矩形,即a=c,b=d,那么代入
 可得平行四边形中
可得平行四边形中

而代入 可得平行四边形面积为
可得平行四边形面积为
如果再是矩形的话 代入上述平行四边形的面积公式,即得矩阵面积公式为:S=ab
代入上述平行四边形的面积公式,即得矩阵面积公式为:S=ab
内接于圆的四边形
四边形内接于圆时,面积最大;事实上,多边形内接于圆时,多边形面积最大。对于四边形内接于圆,会有角A和角C互补,代入 可得
可得
而反过来,由一般四边形有 等号成立(取最值)的条件也很明显,就是内接于圆时。
等号成立(取最值)的条件也很明显,就是内接于圆时。







 本文探讨了四边形的面积计算,从婆罗摩笈多的四边形面积公式出发,通过余弦定理证明了一般四边形的面积表达式。接着,讨论了平行四边形和矩形的面积公式,特别指出矩形面积公式为S=ab。最后,文章阐述了当四边形内接于圆时,其面积达到最大,并给出了相应的证明。
本文探讨了四边形的面积计算,从婆罗摩笈多的四边形面积公式出发,通过余弦定理证明了一般四边形的面积表达式。接着,讨论了平行四边形和矩形的面积公式,特别指出矩形面积公式为S=ab。最后,文章阐述了当四边形内接于圆时,其面积达到最大,并给出了相应的证明。
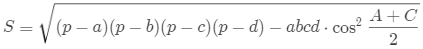

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








