上的介质簇的结构不正确_代数簇的德拉姆上同调

本文讨论代数簇的（代数）德拉姆上同调，为了简单起见，本文只考虑仿射代数簇的情形，尽管本文很多结论对更一般的代数簇（概型）仍然是正确的.

仿射代数簇的定义

设

是一个域，

是一个有限生成

-代数, 称

为

仿射代数簇. 具体来说，若

，那么

，

直观地说，仿射代数簇

无非是仿射空间

中的一组多项式的公共零点集

.

代数德拉姆上同调

设

是

上的代数，仿射代数簇

的

Kahler微分模是指一个

-模

，它是由所有

生成的自由

-模模掉如下关系：

• 常数求导为零：对
  有
  .
• 加性：对
  有
  .
• 莱布尼茨法则：对
  有
  .

得到的

-模，它配备一个

导子：

满足如下泛性：对任意的

-线性导子

(

是

-模), 存在唯一的

-模同态

使得

.

例1：微分摸的计算

设

，那么

就是自由

-模

模掉关系

, i.e.

设

，

-

形式微分模是指

，具体来说，

是

-模

模掉由形如元素

(某两个下标相等) 生成的子模得到的商模. 把

对应的陪集记为

. 如果

是光滑簇，

是秩为

的局部自由

-模，此时

是秩为

的局部自由

-模.

导子

可通过如下方式延拓为

-模同态

：

直接验证可知为

，于是得到复形

, 称之为仿射簇

的

德拉姆复形

:

并把这个复形的同调群称为

的

代数德拉姆上同调, i.e.

有时候简记为

.

例2：特征零的域上的仿射空间的代数德拉姆上同调

设

，则

; 对

,

的每个元素

可写成有限和

的形式，其中

. 若

，则

；如果

，则

.

让我们在这个例子验证一下

：对

,

由于

以及

, 所以

. 而对形式

, 有

由下面将要证明的代数庞加莱引理可知若

, 那么

和对

均有

.

代数庞加莱引理：设

是

特征为零的域，

, 则下列

-模的序列是正合的：

证明：对维数

作归纳. 对

是显然的；假设命题对维数小于

为真，要证对维数

为真.

现设

满足

，要找某形式

使得

. 首先把

以涉不涉及

分成两部分，也就是记

其中

和

均与

无关. 接着定义

这里“积分”

是指形式地替代

中的

为

（这是因为

故包含有理数域，所以总是可以做到的!) . 那么，

以及

这里

不涉及

. 假如能找到某个

使得

，则

就满足要求，而

不涉及

，这表明可以把问题约化为

不涉及

的情形. 于是可以记

由于

, 故对所有

均有

， 因此所有多项式

也不涉及

，这表明可以用归纳假设，证毕.

例3：正特征的域上的仿射空间的代数德拉姆上同调（万恶之源）

如果域

的特征为

，那么庞加莱引理不再成立! 例如考虑

,

, 则序列

不是正合的. 设

是被

整除的正整数，则

不是边界，这是因为

! 这也表明

不是有限维的

-线性空间！

例4：椭圆曲线的代数德拉姆上同调

设

,

为椭圆曲线，其中

没有重根，则

椭圆曲线

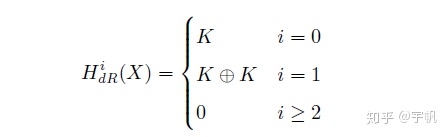
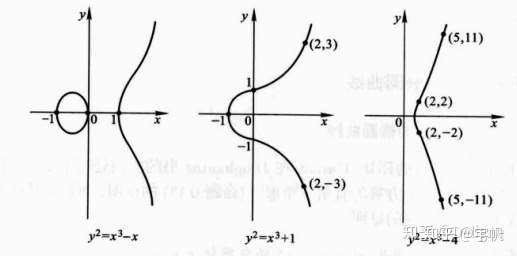
下面定理表明在特征零的域上的光滑代数簇的情形，代数德拉姆上同调给出“正确”的德拉姆上同调！

定理 1（Grothendieck）：设

是

上的光滑代数, i.e.

是光滑代数

-簇, 那么有典范同构

,

其中

是代数簇

相应的复解析流形

的解析德拉姆上同调,

是

的奇异上同调.

证明：见 A. Grohendieck. On the derham cohomology of algebraic varieties. Publications, mathematiques de l'I.H.E.S, 29, 1966. 尽管这个结论对一般的光滑代数簇都是对的，但是最难的一步恰好是仿射的情形！

下面的例子表明上述定理在奇异的代数簇情形不再正确.

例5：奇异曲线代数德拉姆上同调

设

是特征为零的域，

，则

; 对

. 但是当

有

原点处奇异

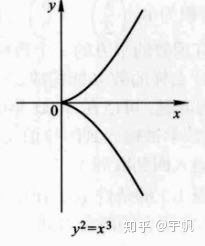
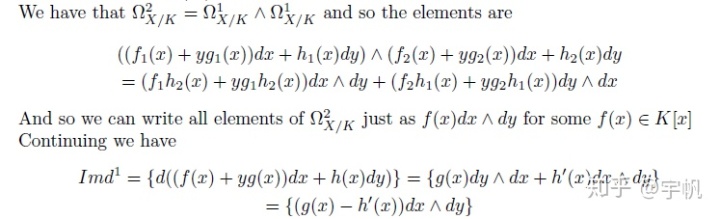
总结一下：

• 当域
  的特征为零，且
  是光滑代数簇，那么它的代数德拉姆上同调
  给出”正确“的德拉姆上同调, i.e.
  , 其中
  是代数簇
  相应的复解析流形
  的解析德拉姆上同调.
• 问题1：当域
  的特征为零，且
  是奇异代数簇，则代数德拉姆上同调不再给出“正确”的德拉姆上同调，见例5.
• 问题2：当域
  为正特征，那么情况非常糟糕，就连仿射直线的
  维代数德拉姆上同调都是无限维的！见例3.

那么如何修正上述问题1和2？

问题1的回答——奇异代数簇的德拉姆上同调

设

是奇异代数

-簇. Deligne 说，我们可以这样干：把

是闭嵌入，

是光滑代数簇 （例如取

为仿射空间） ，如下图所示

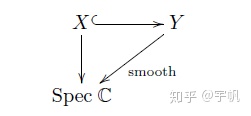
设

为

沿着

作完备化 (

formal completion along

)}. 换句话说，设

是闭嵌入

的定义理想层，令

为

的

-阶加厚, i.e. 理想层

定义的闭子簇. 于是我们有一个序列

它们作为拓扑空间是同一个东西，每个

上有一个德拉姆复形

. 定义

定理 2（Deligne）：在差一个典范同构的意义下，上同调

不依赖于闭嵌入

. 此外，还有典范同构

.

证明：见 Hartshorne, Robin. On the De Rham cohomology of algebraic varieties. Inst. Hautes ´Etudes Sci. Publ. Math. No. 45 (1975), 5–99.

问题2的回答

问题2的回答将我们引向波澜壮阔代数簇的

进上同调理论!