c++ 求四边形面积和周长_8数培优：新题新体验，话说四边形中的动点问题的解题新策略...

动点问题是近几年中考的热点，解此类题型的关键是"化动为静"——寻找运动中的不变量，根据不变量与变量的关系，列出关系式。在解决动点问题时，经常需要多画一些图形，通常一种情况画一个图形，方便把动点转化成一般的几何问题来解决。点的运动问题通常是在三角形、矩形、梯形等一些几何图形上设计一个或两个动点，并对这些动点在运动变化过程中随之产生的等量关系、变量关系，图形的特殊状态、图形间的特殊关系等进行研究。

下面主要讲述的内容主要分为两个类型题目，类型1为由动点产生的函数关系，重点是线段的含参表示，以及自变量的取值范围；类型2为由动点产生的特殊图形，例题主要是从单动点问题过渡到双动点问题，解决问题的主要策略为以静制动，分类讨论，寻找临界点；

类型1：由动点产生的函数关系

1．在长方形ABCD中，AB＝2，BC＝1，动点P从点B出发，沿路线B→C→D做匀速运动，那么△ABP的面积S与点P运动的路程x之间的函数图象大致为( )

【分析】运用动点函数进行分段分析，当P在BC上与CD上时，分别求出函数解析式，再结合图象得出符合要求的解析式．

【解答】：∵AB＝2，BC＝1，动点P从点B出发，P点在BC上时，BP＝x，AB＝2，

∴△ABP的面积S＝1/2×AB×BP＝1/2×2x＝x；

动点P从点B出发，P点在CD上时，△ABP的高是1，底边是2，

所以面积是1，即s＝1；∴S＝x时是正比例函数，且S随x的增大而增大，

S＝1时，是一个常数函数，是一条平行于x轴的直线．所以只有C符合要求．故选：C．

【点评】此题主要考查了动点函数的应用，注意将函数分段分析得出解析式是解决问题的关键．

2．如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止、设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x＝9时，点R应运动到 _______．

【分析】根据点R的移动规律，点R的运动路程为0--4，4--9，9--13，所在线段为PN，QP，QM，那么当x＝9时，点R应运动到高不变的结束，即点Q处．

【解答】当R在PN上运动时，△MNR的面积不断增大；

当R在QP上运动时，MN一定，高为PN不变，此时面积不变；

当R在QM上运动时，面积不断减小．

∴当x＝9时，点R应运动到高不变的结束，即点Q处．

【点评】关键是根据所给函数图象和点的运动轨迹判断出x＝4到9时点所在的位置．

变式．如图1，在矩形ABCD中，AB＝2，动点P从点B出发，沿路线B→C→D作匀速运动，图2是此运动过程中，△PAB的面积S与点P运动的路程x之间的函数图象的一部分，则BC+CD的长为( )

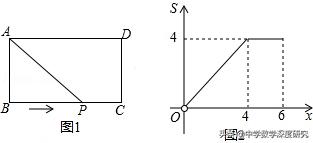
A．3 B．4 C．5 D．6

【解析】由图象2看出当点P到达点C时，即x＝4时，△ABP的面积最大，根据面积公式求出BC的长即可．△ABP的面积＝1/2×AB×BC＝4，

∵AB＝2，∴BC＝4，∴BC+CD＝BC+AB＝4+2＝6故选：D．

3．如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发xs时，△PAQ的面积为ycm²，y与x的函数图象如图②，则线段EF所在的直线对应的函数关系式为________ ．

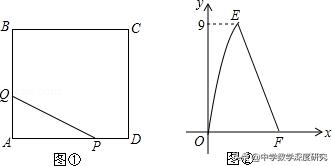
【解析】∵点P沿边DA从点D开始向点A以1cm/s的速度移动；点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．

∴当Q到达B点，P在AD的中点时，△PAQ的面积最大是9cm²，设正方形的边长为acm，

∴1/2×1/2a×a＝9，解得a＝6，即正方形的边长为6，

当Q点在BC上时，AP＝6﹣x，△APQ的高为AB，∴y＝1/2(6﹣x)×6，即y＝﹣3x+18．

故答案为：y＝﹣3x+18(3≤x≤6)．

4．一矩形纸片OABC放在平面直角坐标系中，O为顶点，点A在x轴上，点C在y轴上，OA＝10，OC＝8．

(1)如右上图，在OC边上取一点D，将△BCD沿BD折叠，使点C恰好落在OA边上，记作点E．

①求点E的坐标及折痕BD的长；

②在x轴上取两点M，N(点M在点N的左侧)，且MN＝4.5，求使四边形BDMN的周长最短的点M和点N的坐标；

(2)如右下图，在OC，BC边上分别取点F，G，将△GCF沿GF折叠，使点C恰好落在OA边上，记作点H．设OH＝x，四边形OHGC的面积为S，求S与x之间的函数关系式，并写出自变量x的取值范围．

【解答】(1)①∵四边形OABC为矩形，∴BC＝OA＝10，AB＝OC＝8，

∵△BCD沿BD折叠，使点C恰好落在OA边E点上，∴BC＝BE＝10，DC＝DE，

在Rt△ABE中，BE＝10，AB＝8，

∴AE＝6，∴OE＝10﹣6＝4，∴E点坐标为(4，0)；

在Rt△ODE中，设DE＝x，则OD＝OC﹣DC＝OC﹣DE＝8﹣x，

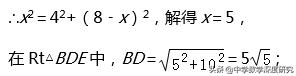
②以D、M、N为顶点作平行四边形DMND′，作出点B关于x轴对称点B′，如图：

∴B′的坐标为(10，﹣8)，DD′＝MN＝4.5，∴D′的坐标为(4.5，3)，

设直线D′B′的解析式为y＝kx+b，

把B′(10，﹣8)，D′(4.5，3)代入得10k+b＝﹣8，4.5k+b＝3，

解得k＝﹣2，b＝12，∴直线D′B′的解析式为y＝﹣2x+12，

令y＝0，得﹣2x+12＝0，解得x＝6，∴M(1.5，0)；N(6，0)．

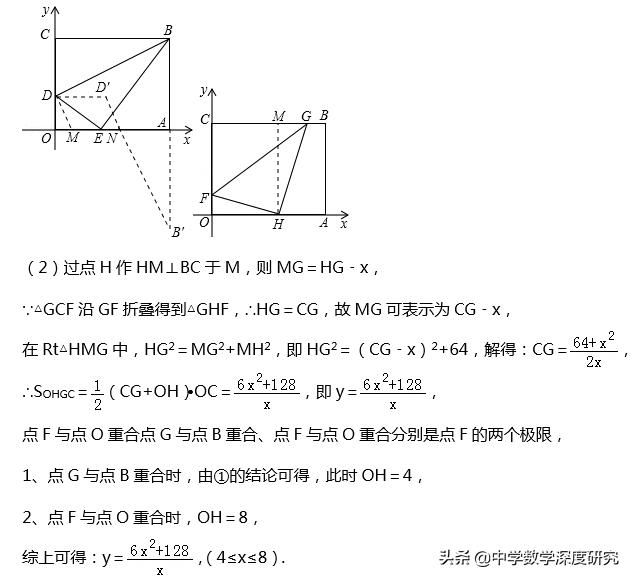
【点评】本题考查了折叠的性质、矩形的性质及最短路径的知识，综合性较强，难度较大，注意掌握折叠前后两图形全等，即对应线段相等，对应角相等，在(2)求自变量范围的时候，要注意寻找极限点，不要想当然的判断．

类型2：由动点产生的特殊图形

我们常见的四边形中的动点问题可以总结为单动点问题与双动点问题．解决问题的主要策略为以静制动，分类讨论，寻找临界点．

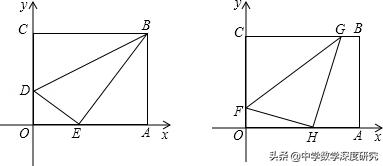
5．如图，在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C的坐标分别为A(10，0)、C(0，4)，点D是OA的中点，点P在BC边上运动，当△ADP为等腰三角形时，点P的坐标为_______ ．

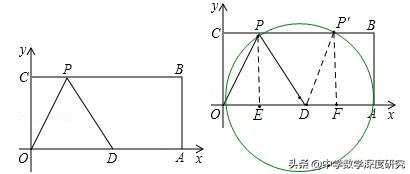
【分析】分PD＝DA，AD＝PA，DP＝PA三种情况讨论，再根据勾股定理求P点坐标

【解答】当PD＝DA,如图：以D为圆心AD长为半径作圆，与BD交P点，P'点∵四边形OABC是长方形，点A、C的坐标分别为A(10，0)、C(0，4)，

∴AD＝PD＝5，PE＝P'F＝4, ∴根据勾股定理得：DE＝DF＝3,

∴P(2，4)，P'(8，4).

若AD＝AP＝5，同理可得P(7，4);

若PD＝PA，则P在AD的垂直平分线上，∴P(7.5，4)

故答案为(2，4)，(8，4)，(7，4)，(7.5，4)

6.如图，在平行四边形ABCD中，点G，H分别是AB，CD的中点，E，F是对角线AC上的两个动点，分别从A，C处同时出发相向而行，到C，A时停止运动．若两动点的速度均为1cm/s，AB＝14cm，BC＝18cm，AC＝24cm，经t秒后，四边形GFHE为矩形，则此时t的值为 _______．

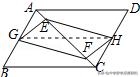
【解答】连接GH，如图所示：

∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，

∵点G，H分别是AB，CD的中点，∴BG＝CH，BG∥CH，

∴四边形BCHG是平行四边形，∴GH＝BC＝18，

当EF＝GH＝18时，平行四边形GFHE是矩形，

分两种情况：

①AE＝CF＝t，EF＝24﹣2t＝18，解得：t＝3；

②AE＝CF＝t，EF＝24﹣2(24﹣t)＝18，解得：t＝21；

综上所述：当t为3s或21s时，四边形EGFH为矩形；

故答案为：3或21．

7.如图，在四边形ABCD中，AD∥BC，DE是BC边上的高，AB＝AD＝5，BC＝12，DE＝4，点P是BC边上一动点，设PB的长为x．

(1)当x的值为_____ 时，四边形APCD为平行四边形；

(2)当x的值为 _____时，四边形APED为矩形；

(3)当△ABP是以AB边为腰的等腰三角形时，求x的值．

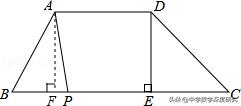
【分析】(1)首先作出AF⊥BC于点F，利用勾股定理求出BF的长，进而利用平行四边形的判定得出答案；

(2)利用矩形的判定得出即可；

(3)利用等腰三角形的判定利用AB＝AP或AB＝BP得出即可．

【解答】(1)过点A作AF⊥BC于点F，

∵在四边形ABCD中，AD∥BC，DE是BC边上的高，AB＝AD＝5，BC＝12，DE＝4，∴AF＝4，EF＝5，∴由勾股定理可求得BF＝3，

当AD∥ PE，AD=PE,时，四边形APCD为平行四边形，

即PC＝AD＝5时，x＝BP＝12﹣5＝7，四边形APCD为平行四边形；

(2)当BF＝BP＝3时，当BF＝BP＝3时，AD∥ PE，AD=PE,∠APE＝90°时，四边形APED为矩形，∠APE＝90°时，四边形APED为矩形；

(3)当AB＝AP＝5时，

BF＝3，则BP＝6，即x＝6时，△ABP是等腰三角形，

当AB＝BP＝5时，即x＝5时，△ABP是等腰三角形；

综上所述：x＝6或5时，△ABP是以AB边为腰的等腰三角形．

故答案为：7；3．

8.如图，在平行四边形ABCD中，已知对角线AC、BD相交于点O，若E、F是AC上两动点，分别从A、C两点以相同的速度1cm/s向点O运动．

(1)当E与F不重合时，四边形DEBF是否是平行四边形？请说明理由；

(2)若AC＝16cm，BD＝12cm，点E，F在运动过程中，四边形DEBF能否为矩形？如能，求出此时的运动时间t的值，如不能，请说明理由．

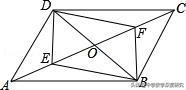
【分析】(1)判断四边形DEBF是否为平行四边形，需证明其对角线是否互相平分；已知了四边形ABCD是平行四边形，故OB＝OD；而E、F速度相同，方向相反，故OE＝OF；由此可证得BD、EF互相平分，即四边形DEBF是平行四边形；

(2)若以D、E、B、F为顶点的四边形是矩形，则必有BD＝EF，可据此求出时间t的值．注意有两解；

【解答】(1)当E与F不重合时，四边形DEBF是平行四边形

理由：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD；

∵E、F两动点，分别从A、C两点以相同的速度向C、A运动，

∴AE＝CF；∴OE＝OF；∴BD、EF互相平分；∴四边形DEBF是平行四边形；

(2)∵四边形DEBF是平行四边形，

∴当BD＝EF时，四边形DEBF是矩形；

∵BD＝12cm，∴EF＝12cm；∴OE＝OF＝6cm；

∵AC＝16cm；∴OA＝OC＝8cm；∴AE＝2cm或14cm，

由于动点的速度都是1cm/s，所以t＝2(s)或14(s)

故当运动时间t＝2s或14s时，以D、E、B、F为顶点的四边形是矩形．