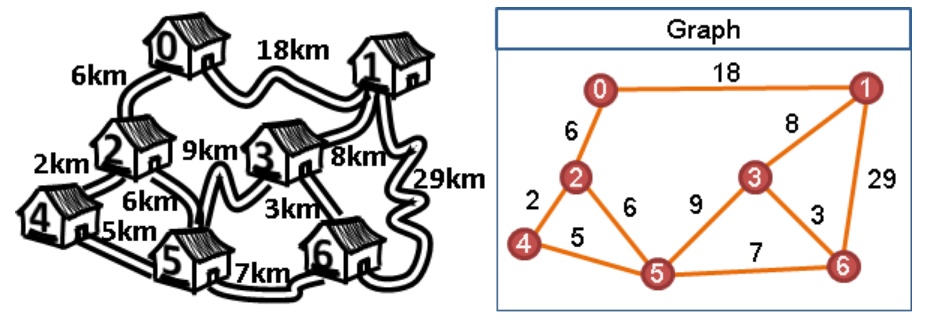
《自动驾驶路径规划-Graph-Based的BFS最短路径规划》中提到我们可以将地图抽象为Graph的数据结构,然后利用Graph的广度优先遍历算法(Breadth-First Search, BFS)解决无权重的High-Level的地图级别的规划。但是实际应用场景中,地图中各个路径所代表的Graph的边的权重都是不同的,比如距离长的Edge权重就应该比较低;交通拥堵的Edge权重就应该低等等。对于有权重的Graph如何进行最短路径规划呢,Dijkstra算法可以解决这个问题。

1、什么是Dijkstra算法
Dijkstra算法是一种有权图(Graph)的单源最短路径求解算法,给定一个起点,使用Dijkstra算法可以得到起点到其它所有节点的最短路径。Dijkstra算法要求图(Graph)中所有边的权重都为非负值,只有保证了这个条件才能该算法的适用性和正确性。
2、Dijkstra算法Overview
假设有权图(Graph)的如下,起点(Starting Node)为0,我们一步步看看如何使用Diskstra算法计算起点(Starting Node)到达所有其它Node的最短路径。

首先我们需要定义一个数据结构来记录起点(Starting Node)到其它所有Node的最短距离,并将所有最短距离的值初始化为正的无穷大,表示各个节点(Node)均不可达。
dist = [infinity, infinity, ..., infinity]然后,需要定义一个(index, distance)的Pair对象来存储起点(Starting Node)到index Node的当前最短距离,其中index为顶点的索引,distance为index Node到Starting Node的最短距离。在开始进行路径搜索前,所有Node对应的最短距离都初始化为正的无穷大。
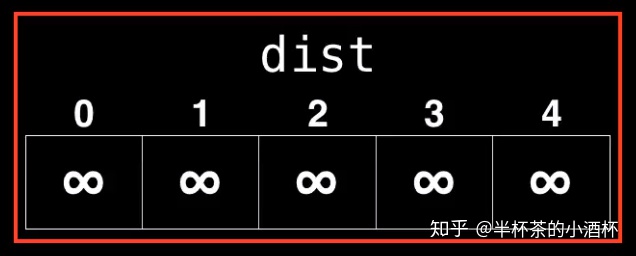
在图的路径搜索过程中,我们需要先搜索距离最近的节点,所以我们需要使用优先级队列(Priority Queue)或者小顶堆(Min Heap)的数据结构来存储(index, distance)的Pair,保证每次取出的待访问Node都是距离起点(Starting Node)最近的Node。
准备好数据结构之后,开始算法执行过程:
1、首先将起点(Starting Node)=(0, 0)放入优先级队列(Priority Queue),表明我们从index=0的节点开始查找,该节点距离起点(Starting Node)的distance = 0;

此时优先级队列(Priority Queue)的内容如下:

2、从优先级队列(Priority Queue)中取出distance最小的Node(此时index=0的Node的distance最小),遍历它的所有Neighbor节点。
首先遍历index=1的Node,该Node未被访问过,所以直接更新起点(Starting Node)到index = 1的Node的最短距离为4,并且放入到优先级队列中(Priority Queue)中;
然后遍历index=4的Node,该Node未被访问过,所以直接更新Starting Node到index=2的最短距离为1,并且放入到优先级队列中(Priority Queue)中;
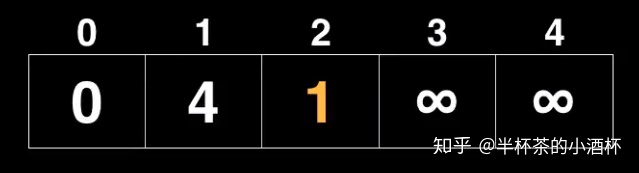
此时优先级队列(Priority Queue)的内容如下:

3、从优先级队列(Priority Queue)中取出distance最小的Node(此时index=2的Node的distance最小),遍历它的所有Neighbor节点。
首先遍历index=1的Node,由于index=1的Node已经被访问过,此时需要比较当前的距离是否小于已有的距离。起点(Starting Node)到index =1的distance为1 + 2 =3,小于已有的起点(Starting Node)直接到index=1的Node的distance = 4,因此更新起点(Starting Node)到index=1的distance为3。
然后遍历index=3的Node,该Node未被访问过,所以直接更新其到起点(Starting Node)的distance为1+ 5 = 6。
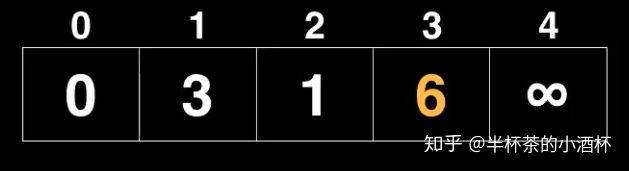
此时优先级队列(Priority Queue)的内容如下:

4、从优先级队列(Priority Queue)中取出距离最小的Node(此时index=1的Node的distance最小),遍历它的所有Neighbor节点。
遍历index=3的Node,起点(Starting Node)到index=3的Node距离为3 + 1 = 4,小于原有起点(Starting Node)经由index=2的到达index=3的Node的距离6,所以从更新起点(Starting Node)到index=3的Node的最短距离为4。

此时优先级队列(Priority Queue)的内容如下:

5、从优先级队列(Priority Queue)中取出距离最小的Node(此时index=3的Node的distance最小),遍历它的所有Neighbor节点。
遍历到index=4的Node,该Node尚未被遍历过,起点(Starting Node)到index=4的Node最短距离为4 + 3 = 7;。
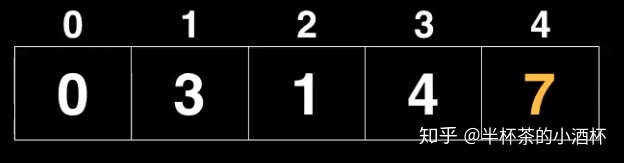
此时优先级队列(Priority Queue)的内容如下:

这就是Dijkstra算法的完整执行过程,至此我们得到了从起点(Starting Node)到所有其它Node的最短距离。
3、Dijkstra算法实现路径查找
因为我们的目标是搜索从起点到目的地的最短路径,而Dijkstra算法提供了从起点(Starting Node)到其它所有节点的最短路径,所以我们在路径查找中对Dijkstra算法做了剪枝处理。
def extractPath(self, u, pred):
path = []
k = u
path.append(k)
while k in pred:
path.append(pred[k])
k = pred[k]
path.reverse()
return path
def findShortestPathInWeightGraph(self, start, end):
# Mark all the vertices as not visited
closed = set()
pq = queue.PriorityQueue()
pred = {}
min_dist = {}
pq.put((0,start))
min_dist["0"] = 0
while pq.qsize() != 0:
dist, u = pq.get()
closed.add(u)
if u == end:
path = self.extractPath(u, pred)
return path
for to_node, to_weight in self.__graph_dict[u].items():
if to_node in closed:
continue;
newdist = dist + to_weight
if to_node in min_dist:
if newdist < min_dist[to_node] :
min_dist[to_node] = newdist
pred[to_node] = u
else:
min_dist[to_node] = newdist
pred[to_node] = u
pq.put((newdist, to_node))构造如图2.1的Graph,测试代码如下:
g = { "0" : {"1":4, "2":1},
"2" : {"1":2, "3":5},
"1" : {"3":1},
"3" : {"4":3}
}
graph = Graph(g)
print('The path from vertex "0" to vertex "3":')
path = graph.findShortestPathInWeightGraph("0", "3")
print(path)路径检索结果如下:
The path from vertex "0" to vertex "3":
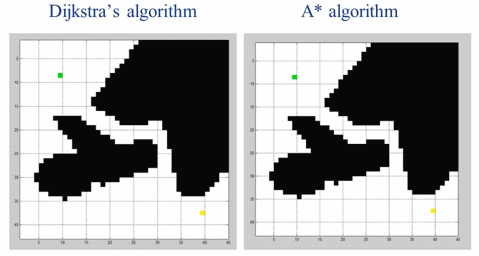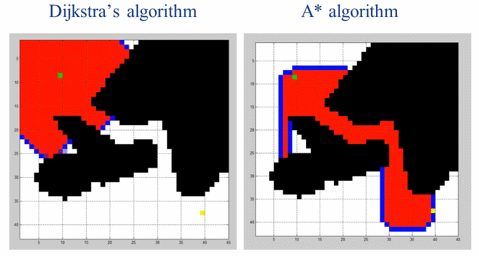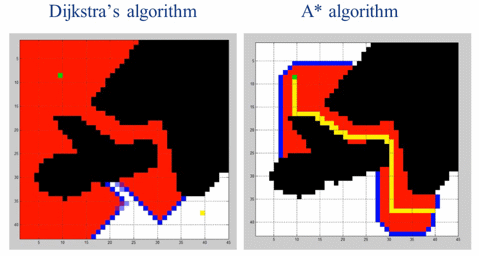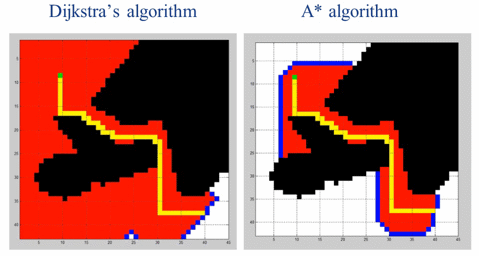
['0', '2', '1', '3']作为运动规划领域最著名的算法之一,Dijkstra算法可以解决带权重有向图的最短路径规划问题,在实际的路径规划中也有大规模的实际应用。但是Dijkstra算法的搜索没有方向性,会有大量冗余的搜索操作。我们可以给Dijkstra加上一些启发性的信息,引导搜索算法快速的搜索到目标,这就是A*算法。
由于加入引导信息,A*算法在大多数情况下会比Dijkstra算法要快。
参考链接
1、[运动规划-简介篇](运动规划 | 简介篇)
2、Dijkstra's Shortest Path Algorithm | Graph Theory
注:本文首发于微信公众号,转载请注明出处,谢谢!

个人博客地址:
http://www.banbeichadexiaojiubei.comwww.banbeichadexiaojiubei.com推荐阅读:
半杯茶的小酒杯:自动驾驶路径规划-Graph Based的BFS最短路径规划zhuanlan.zhihu.com





















 6536
6536











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








